本文主要是介绍主题模型LDA教程:一致性得分coherence score方法对比(umass、c_v、uci),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 主题建模
- 潜在迪利克雷分配(LDA)
- 一致性得分 coherence score
- 1. CV 一致性得分
- 2. UMass 一致性得分
- 3. UCI 一致性得分
- 4. Word2vec 一致性得分
- 5. 选择最佳一致性得分
主题建模
主题建模是一种机器学习和自然语言处理技术,用于确定文档中存在的主题。它能够确定单词或短语属于某个主题的概率,并根据它们的相似度或接近度对文档进行聚类。它通过分析文档中单词和短语的频率来实现这一目的。 主题建模的一些应用还包括文本摘要、推荐系统、垃圾邮件过滤器等。
具体来说,目前用于提取主题模型的方法包括潜狄利克特分配法(LDA)、潜语义分析法(LSA)、概率潜语义分析法(PLSA)和非负矩阵因式分解法(NMF)。我们将重点讨论潜狄利克特分配(LDA)的一致性得分。
潜在迪利克雷分配(LDA)
Latent Dirichlet Allocation 是一种无监督的机器学习聚类技术,我们通常将其用于文本分析。它是一种主题建模,其中单词被表示为主题,而文档则被表示为这些单词主题的集合。
总之,这种方法通过几个步骤来识别文档中的主题:
- 抽取主题–在主题空间中初始化文档的
Dirichlet分布,并从文档主题的多叉分布中选择 N 个主题。 - 抽取单词并创建文档 - 在单词空间中初始化主题的
Dirichlet分布,并从主题上单词的多项式分布中为每个先前抽取的主题选择 N 个单词。 - 最大化创建相同文档的概率。
上述算法的数学定义为
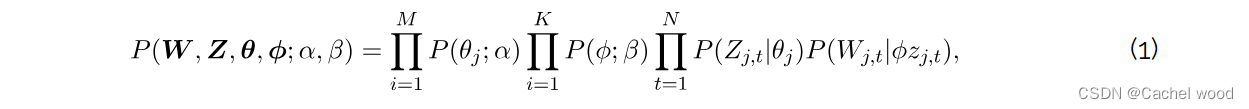
其中 α \alpha α 和 β \beta β 定义了 Dirichlet 分布, θ \theta θ 和 ϕ \phi ϕ 定义了多叉分布, Z Z Z 是包含所有文档中所有单词的主题向量, W W W 是包含所有文档中所有单词的向量, M M M 个文档数, K K K 个主题数和 N N N 个单词数。
我们可以使用吉布斯采样(Gibbs sampling)来完成整个训练或概率最大化的过程,其总体思路是让每个文档和每个单词尽可能地单色。基本上,这意味着我们希望每篇文档的文章数越少越好,每个词属于的主题数越少越好。
一致性得分 coherence score
在主题建模中,我们可以使用一致性得分来衡量主题对人类的可解释性。在这种情况下,主题表示为属于该特定主题概率最高的前 N 个词。简而言之,一致性得分衡量的是这些词之间的相似程度。
1. CV 一致性得分
最流行的一致性度量之一被称为 CV。它利用词的共现创建词的内容向量,然后利用归一化点式互信息(NPMI)和余弦相似度计算得分。这个指标很受欢迎,因为它是 Gensim 主题一致性pipeline模块的默认指标,但它也存在一些问题。即使是该指标的作者也不推荐使用它。
不推荐使用 CV 一致性度量。
2. UMass 一致性得分
我们建议使用 UMass 一致性评分来代替 CV 评分。它计算两个词 w i w_{i} wi 和 w j w_{j} wj 在语料库中同时出现的频率,其定义为
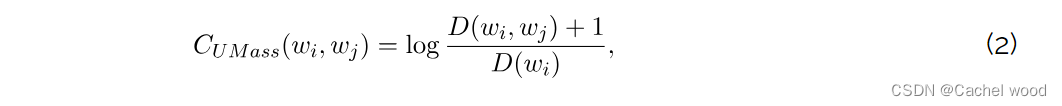
其中, D ( w i , w j ) D(w_{i}, w_{j}) D(wi,wj) 表示单词 w i w_{i} wi 和 w j w_{j} wj 在文档中同时出现的次数, D ( w i ) D(w_{i}) D(wi) 表示单词 w i w_{i} wi 单独出现的次数。数字越大,一致性得分越高。此外,这一指标并不对称,也就是说 C U M a s s ( w i , w j ) C_{UMass}(w_{i}, w_{j}) CUMass(wi,wj)不等于 C U M a s s ( w j , w i ) C_{UMass}(w_{j}, w_{i}) CUMass(wj,wi)。我们用描述主题的前 N 个词的平均成对一致性得分来计算主题的全局一致性。
3. UCI 一致性得分
该一致性得分基于滑动窗口和所有词对的点互信息,使用出现率最高的 N 个词。我们不计算两个词在文档中出现的频率,而是使用滑动窗口计算词的共现。也就是说,如果我们的滑动窗口大小为 10,那么对于一个特定的词 w i w_{i} wi,我们只能观察到词 w i w_{i} wi 前后的 10 个词。
因此,如果单词 w i w_{i} wi 和 w j w_{j} wj 同时出现在文档中,但它们没有同时出现在一个滑动窗口中,我们就不认为它们是同时出现的。同样,对于 UMass 分数,我们将单词 w i w_{i} wi 和 w j w_{j} wj 之间的 UCI 一致性定义为
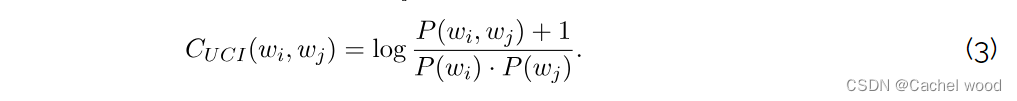
其中, P ( w ) P(w) P(w) 是在滑动窗口中看到单词 w 的概率, P ( w i , w j ) P(w_{i}, w_{j}) P(wi,wj)是单词 w i w_{i} wi 和 w j w_{j} wj 在滑动窗口中同时出现的概率。在原论文中,这些概率是使用 10 个单词的滑动窗口,从 200 多万篇英文维基百科文章的整个语料库中估算出来的。我们计算话题全局一致性的方法与计算 UMass 一致性的方法相同。
4. Word2vec 一致性得分
一个聪明的想法是利用 word2vec 模型来计算一致性得分。这将在我们的得分中引入单词的语义。基本上,我们希望根据两个标准来衡量一致性:
主题内相似性–同一主题中词语的相似性。
主题间相似性–不同主题中词语的相似性。
这个想法非常简单。我们希望主题内相似度最大化,主题间相似度最小化。此外,我们所说的相似性是指 word2vec 嵌入所代表的词与词之间的余弦相似性。
然后,我们计算每个主题的主题内相似度,即该主题中每对可能的前 N 个词之间的平均相似度。随后,我们计算两个主题之间的主题间相似度,即这两个主题中前 N 个词之间的平均相似度。
最后,两个主题 t i t_{i} ti 和 t j t_{j} tj 之间的 word2vec 一致性得分计算公式为
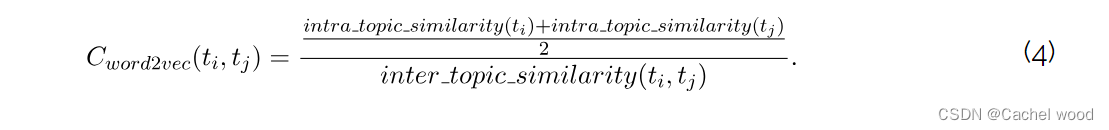
5. 选择最佳一致性得分
**没有一种方法可以确定一致性得分的好坏。**得分及其价值取决于计算数据。例如,在一种情况下,0.5 的分数可能足够好,但在另一种情况下则不可接受。唯一的规则是,我们要最大限度地提高这个分数。
通常,一致性得分会随着主题数量的增加而增加。随着主题数量的增加,这种增加会变得越来越小。可以使用所谓的肘部技术来权衡主题数量和一致性得分。这种方法意味着将一致性得分绘制成主题数量的函数。我们利用曲线的肘部来选择主题数量。
这种方法背后的理念是,我们要选择一个点,在这个点之后,一致性得分的递减增长不再值得额外增加主题数。n_topics = 3 时的肘截点示例如下:
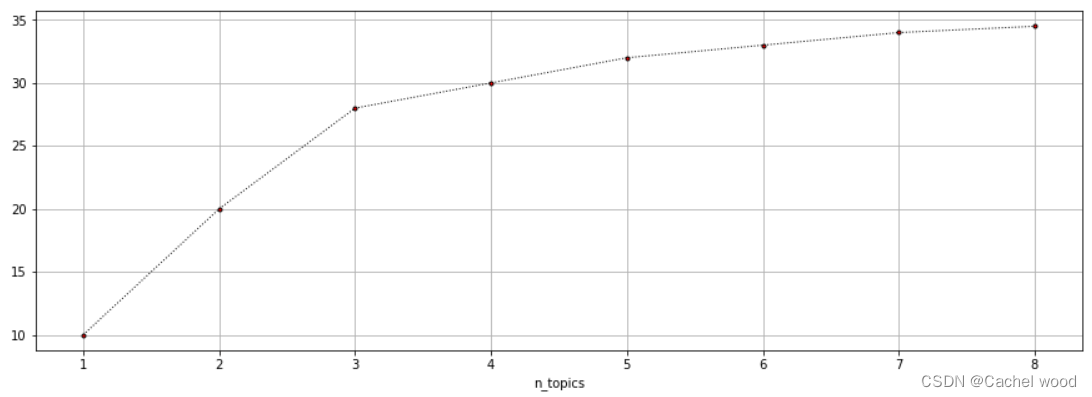
肘 elbow rule
此外,一致性得分取决于 LDA 超参数,如 α \alpha α、 β \beta β 和 K K K。毕竟,手动验证结果是很重要的,因为一般来说,无监督机器学习系统的验证工作都是由人工完成的。
这篇关于主题模型LDA教程:一致性得分coherence score方法对比(umass、c_v、uci)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



