本文主要是介绍图解、手撕十大排序算法[思路清晰版],希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
常见的排序算法有冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、桶排序、计数排序、基数排序等。其中最熟悉的是冒泡排序,记得笔者第一次接触冒泡排序还是2008年参加学校的ACM比赛之前学习的,其他排序基本都是在面试、考研等考试中遇到,最晚接触的是计数排序,是在2017年读研后上的《算法分析与设计》这门课中接触。其中最熟悉的是冒泡排序,因为接触时间长,也最简单。其他的排序算法基本思想也了解一点,有些细节可能会有遗漏,最近在程序界流行一个词–“手撕”,下面先讲一下有关排序算法的性质,然后手撕这几种常见的排序算法。
专业术语说明
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
内排序:所有排序操作都在内存中完成;
外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
时间复杂度: 一个算法执行所耗费的时间。
空间复杂度:运行完一个程序所需内存的大小。
笔者发现平常最容易考察的就是排序算法对比,先将排序算法对比列表如下:
| 排序算法 | 平均时间复杂度 | 最好情况下时间复杂度 | 最坏情况下时间复杂度 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | in-place | 稳定 |
| 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | in-place | 不稳定(每趟选择最小的和待插入位置互换) |
| 插入排序 | O(n2) | O(n) | O(n2) | O(1) | in-place | 稳定 |
| 希尔排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | in-place | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | out-place | 稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n2) | O(logn) | in-place | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | in-place | 不稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | out-place | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | O(n2) | O(n+k) | out-place | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | out-place | 稳定 |
n: 数据规模 k:“桶”的个数 In-place: 占用常数内存,不占用额外内存 Out-place: 占用额外内存
图解10种排序算法:
1.冒泡排序
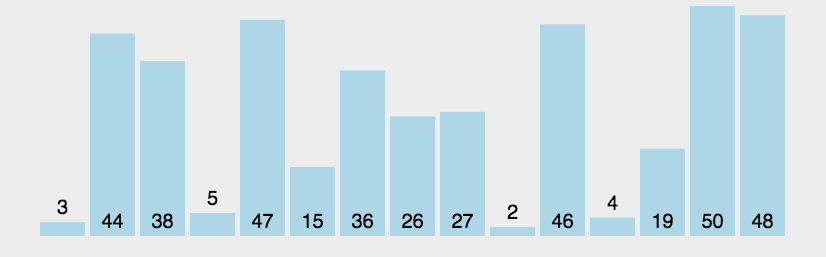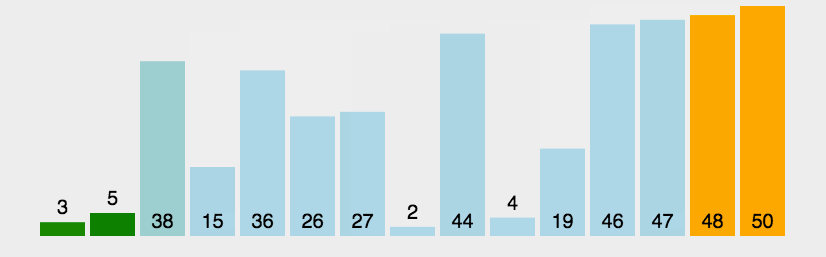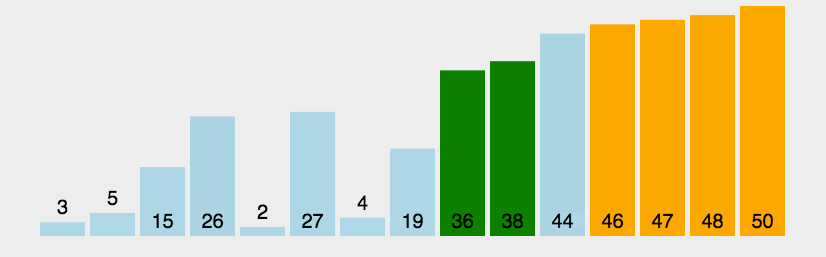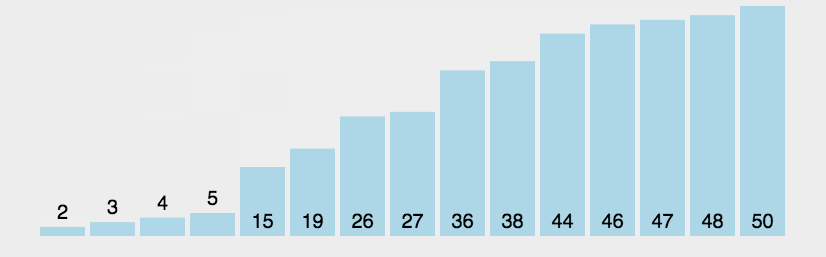
2.选择排序
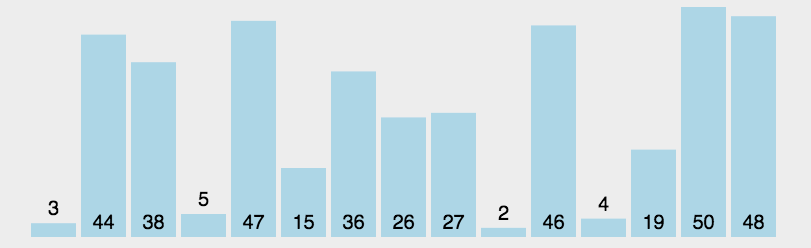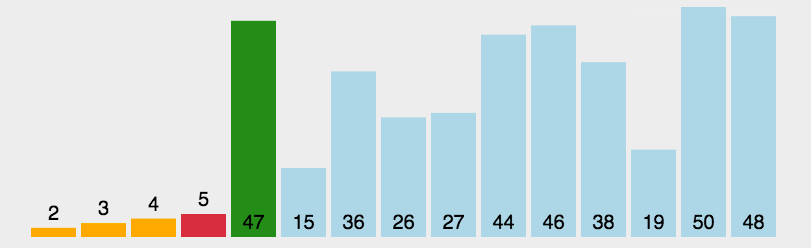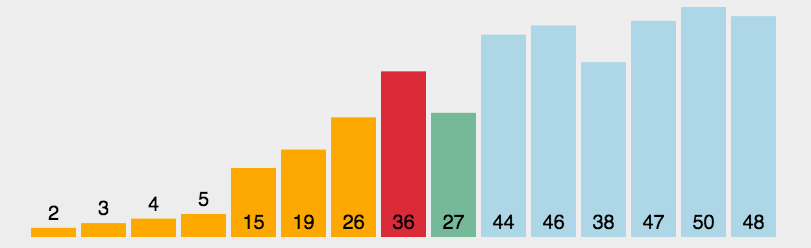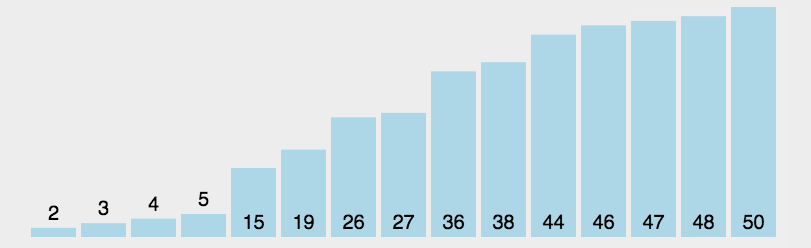
3.插入排序
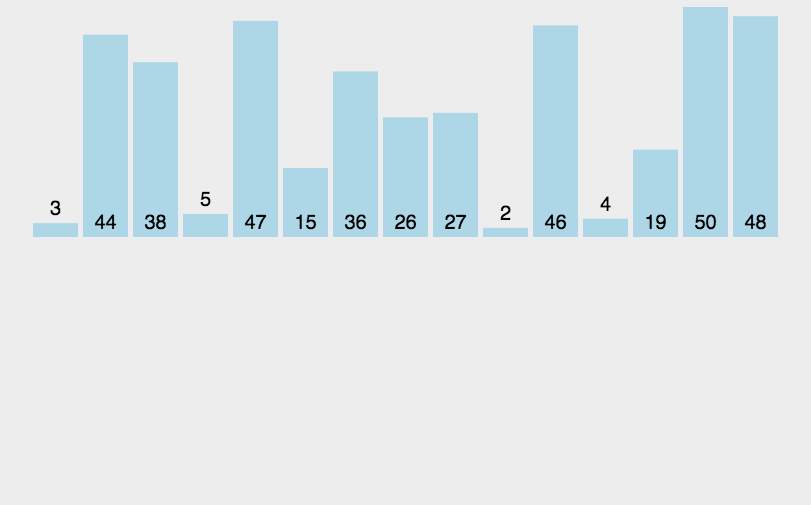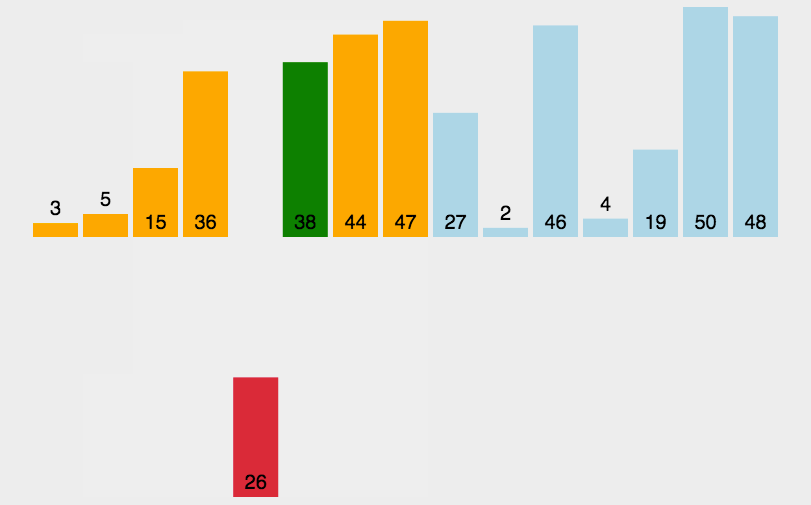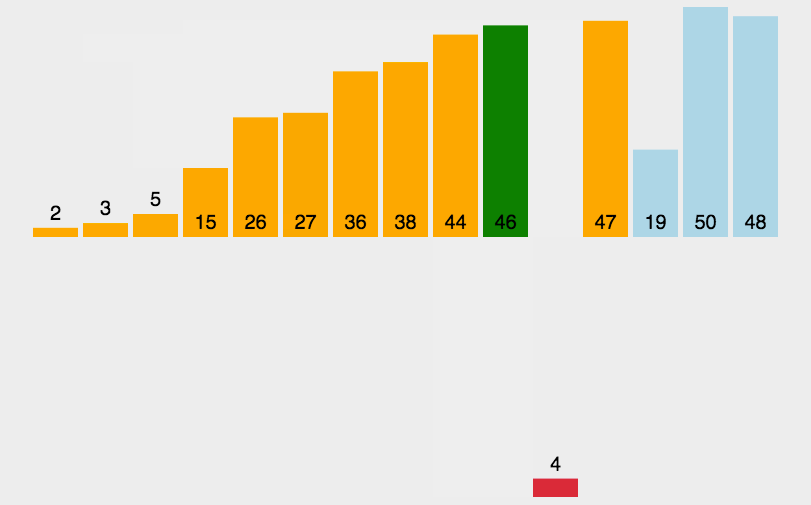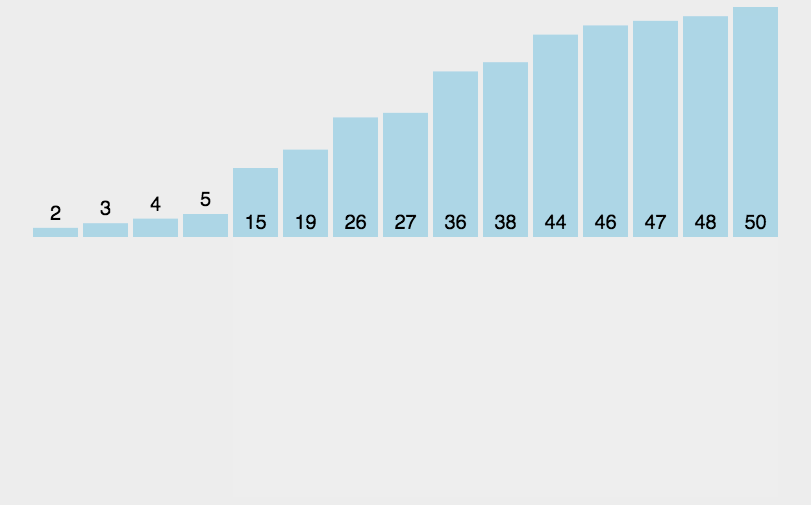
4.希尔排序
5.归并排序
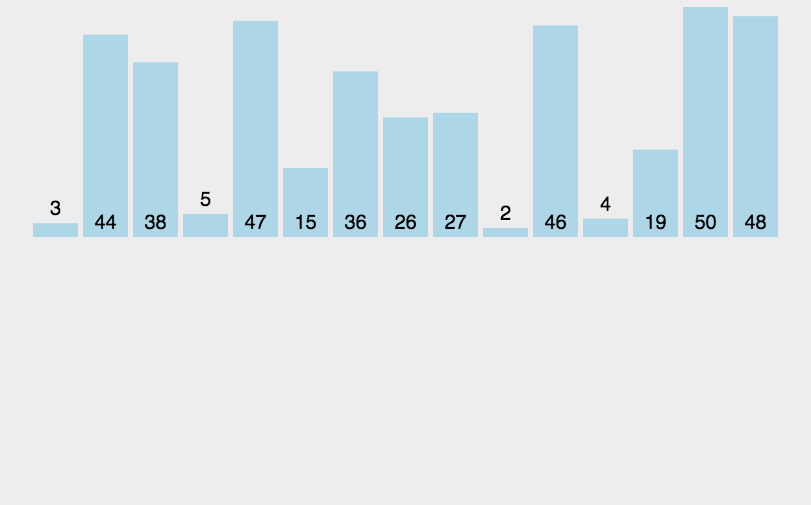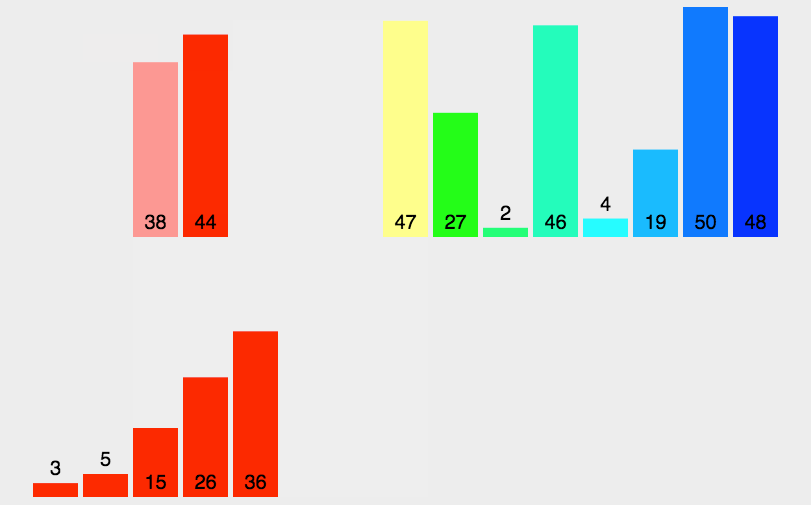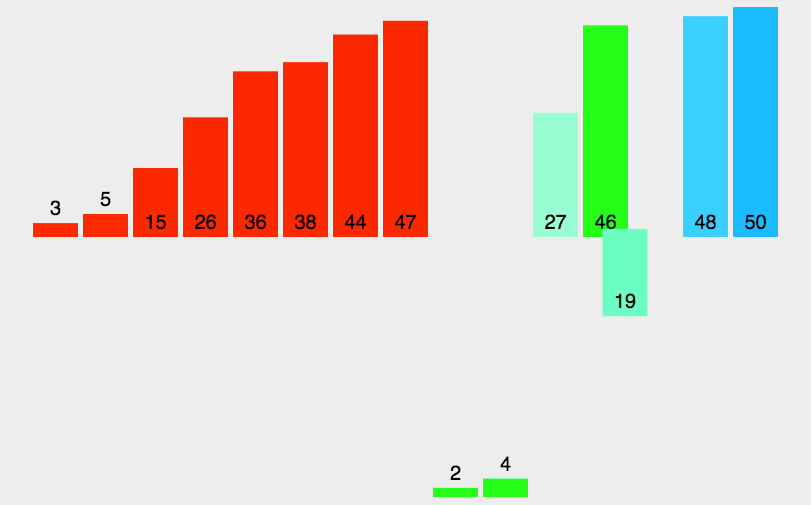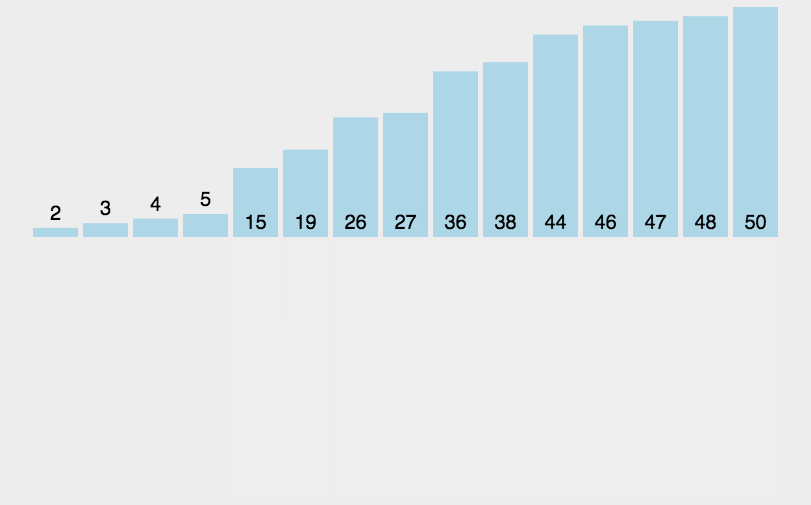
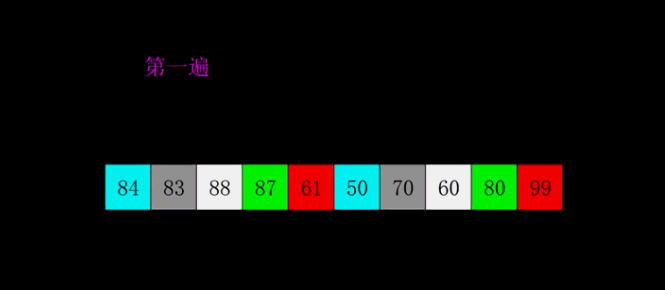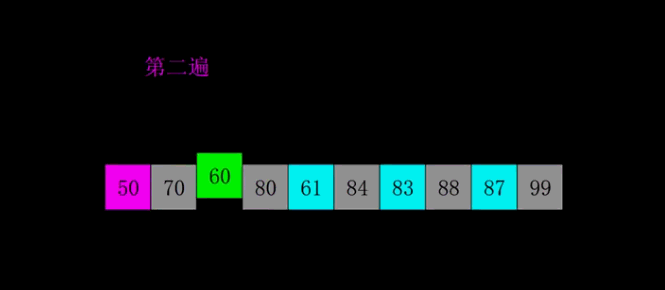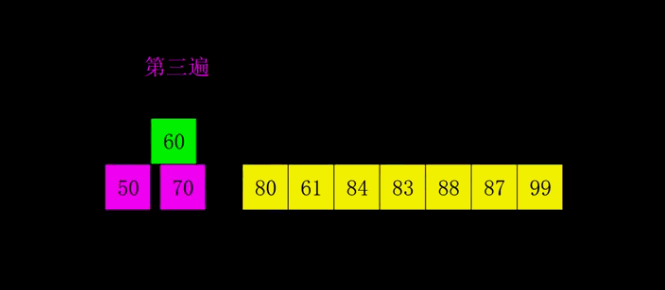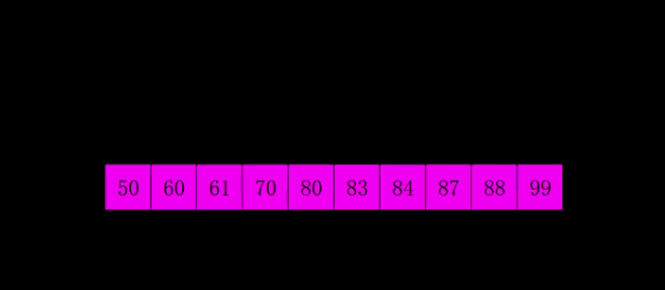
6.快速排序
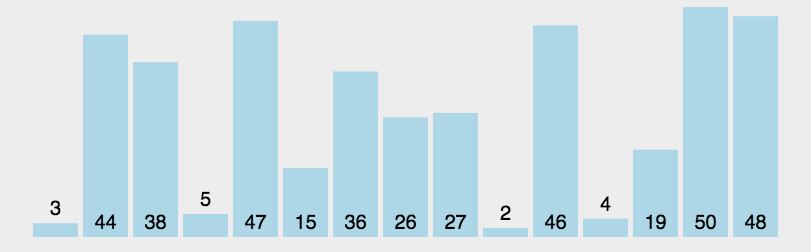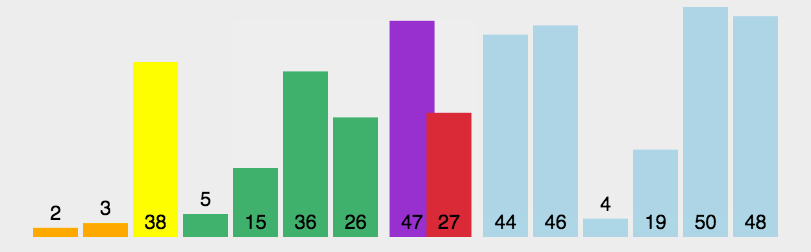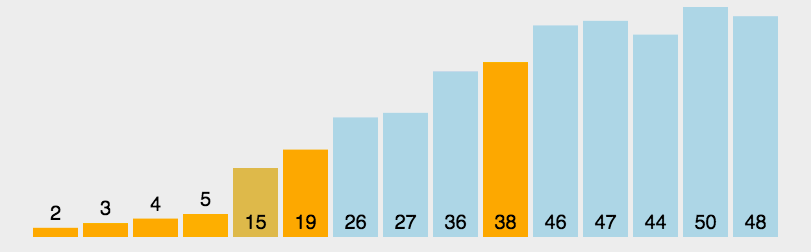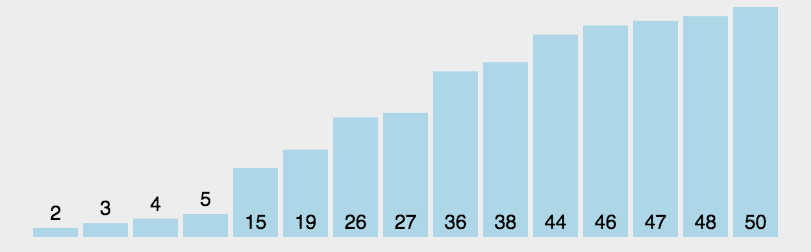
7.堆排序

8.桶排序

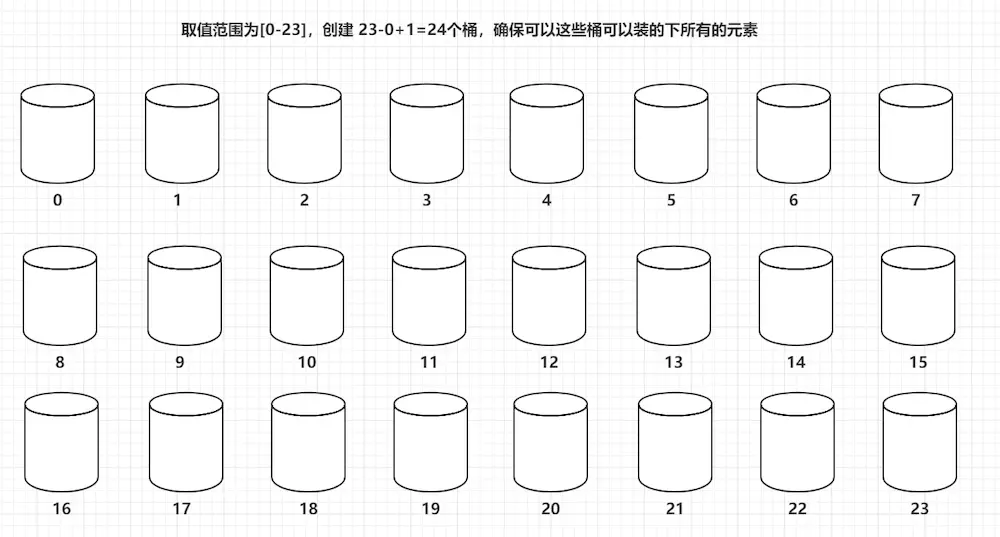
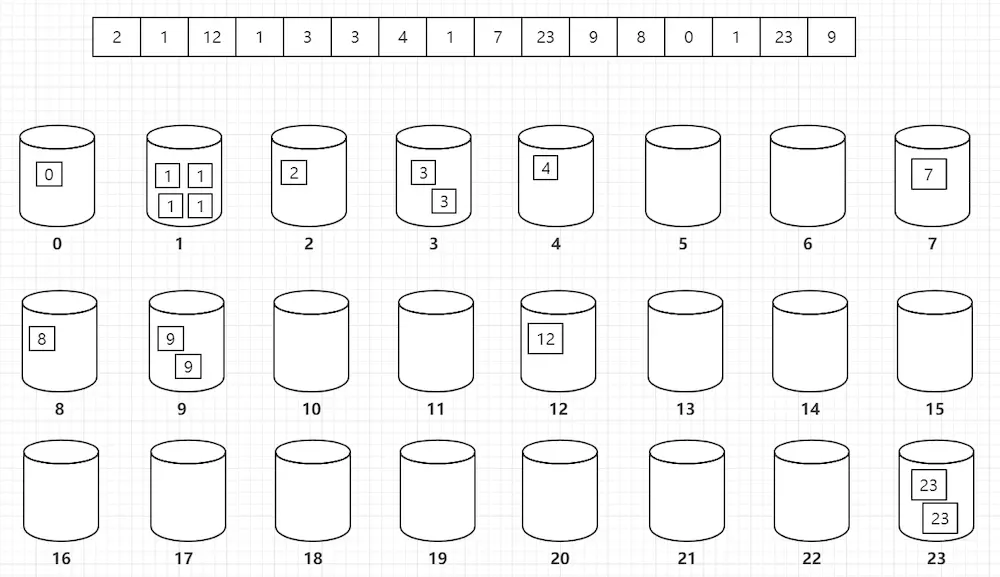 9.计数排序
9.计数排序
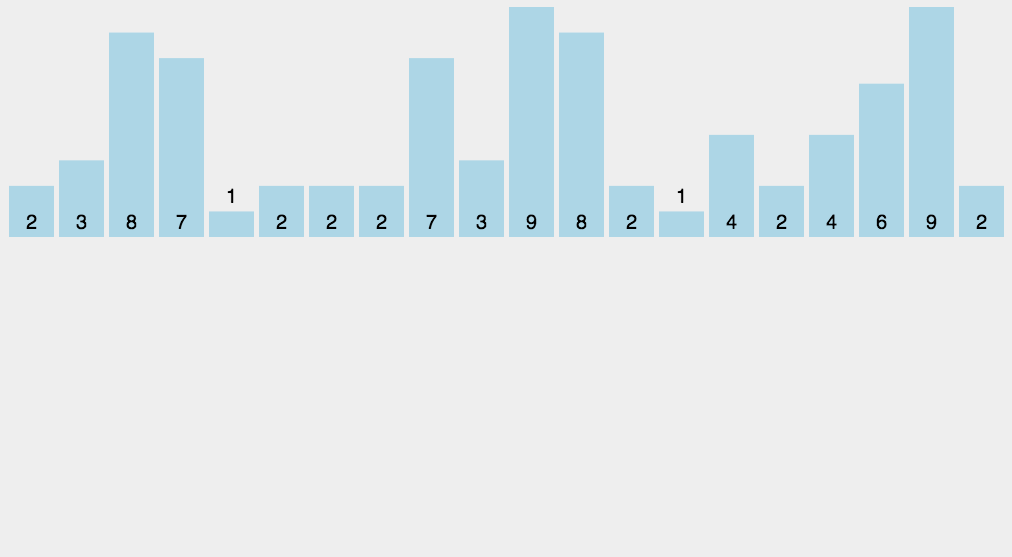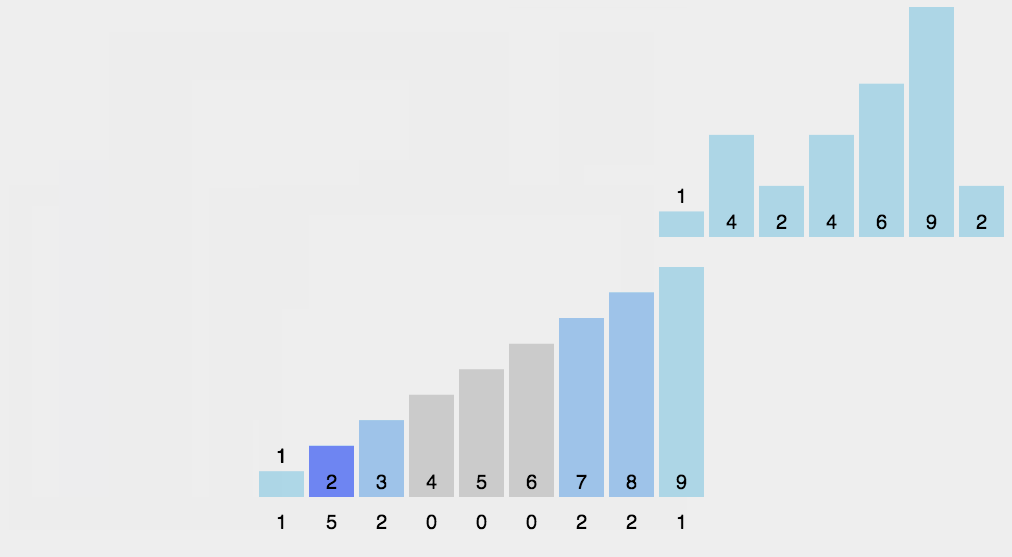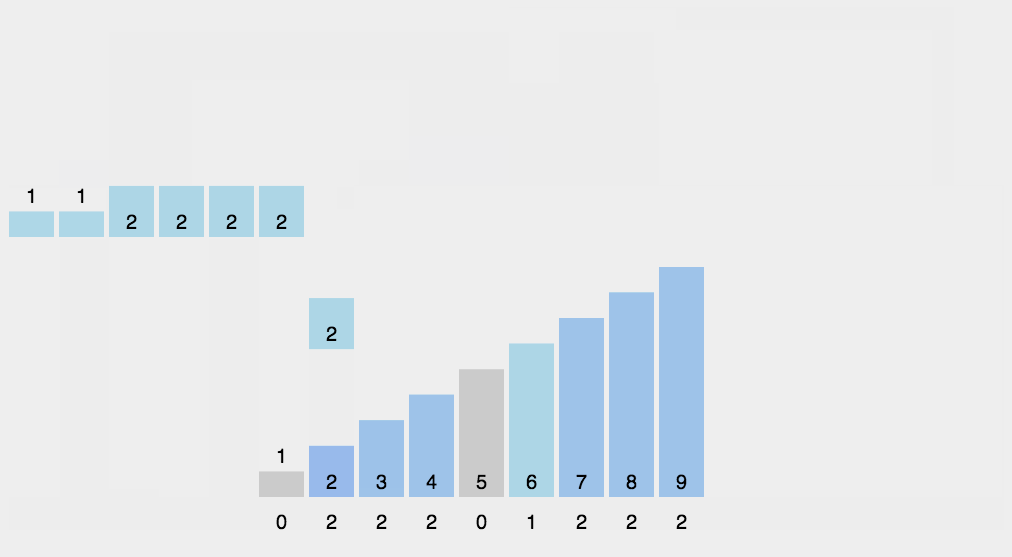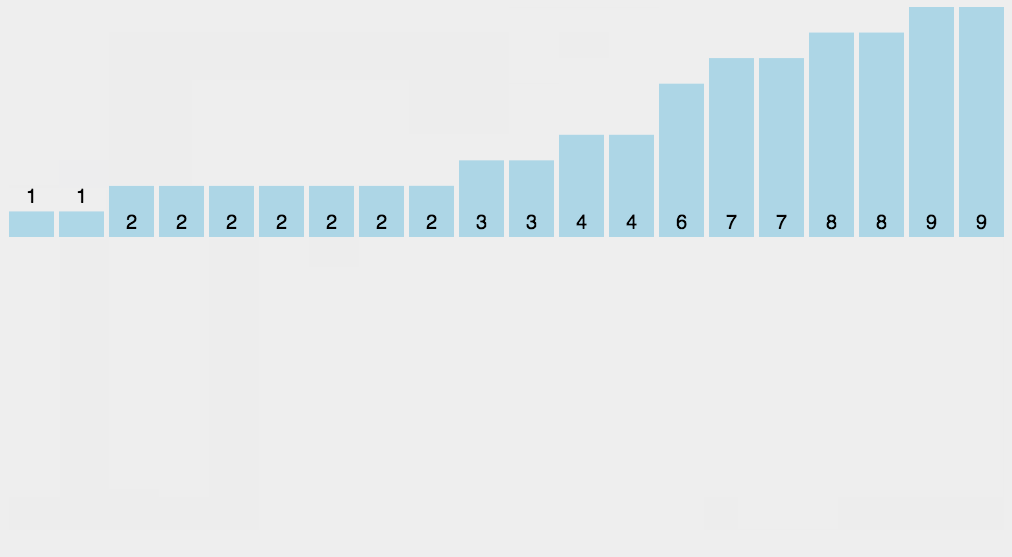
10.基数排序

package rank;import java.util.ArrayList;
import java.util.Collections;public class CehRank {//1.冒泡排序<时间复杂度O(n*n),空间复杂读O(n),稳定排序>public static void bubbleSort(int[] data) {int len = data.length;int lastSwap = len;//记录最后一次交换的位置for(int i = 0; i<len; i++) {boolean hasSwap = false;int sortBorder = lastSwap ;// 无序数列的边界,每次比较只需要比到这里为止for(int j=1; j<sortBorder; j++) {if(data[j]<data[j-1]) {int tmp = data[j];data[j] = data[j-1];data[j-1] = tmp;hasSwap = true;// 有元素交换lastSwap = j;// 最后一次交换元素的位置}}if(!hasSwap) {break;//如果在这一趟内排序没有发生交换,说明数组已经有序,直接退出}}}//2.选择排序<时间复杂度O(n*n),空间复杂度O(n),不稳定排序>public static void selectSort(int[] data) {int len = data.length;for(int i=0; i<len; i++) {int min=i;for(int j=i+1; j<len; j++) {if(data[j]<data[min]) {min = j;}}int tmp = data[min];data[min] = data[i];data[i] = tmp;}}//3.插入排序<时间复杂度O(n*n),空间复杂度O(1),稳定排序>public static void insertSort(int[] data) {int len = data.length;for(int i=1; i<len; i++) {//需要待插入的数int value = data[i];//待插的数据int j =0;//待插入的位置for( j=i-1; j>=0; j--) {if(value<data[j]) {data[j+1] = data[j];} else {break;}}data[j+1] = value;}}//4、希尔排序:插入排序改进版<时间复杂度O(n*log(n)),空间复杂度O(1),不稳定排序>public static void hillSort(int[] data) {int len = data.length;int gap = 1;while(gap<len/3) {gap *= 3+1;}while(gap>0) {for(int i=gap; i<len; i++) {int currentIndex = i;int pIndex = currentIndex - gap;while(pIndex>=0) {if( data[currentIndex]<data[pIndex] ) {int tmp = data[currentIndex] ;data[currentIndex] = data[pIndex];data[pIndex] = tmp;}currentIndex = pIndex;pIndex -= gap;}}gap = (int)Math.floor(gap/3);}}//5.归并排序<时间复杂度O(n*log(n)),空间复杂度O(n),稳定排序>public static void mergeSort(int[] data) {divideMerge(data, 0, data.length-1);}//归并排序:分解public static void divideMerge(int[] data, int start, int end) {if(end<=start) {return;}int mid = (start+end)/2;divideMerge(data, start, mid);divideMerge(data, mid+1, end); merge(data, start, mid, end);}//归并排序:合并private static void merge(int[] data, int start, int middle, int end) {int len = data.length;int[] temp = new int[len];//复制要合并的数据for(int i=start; i<= end; i++) {temp[i] =data[i];}int left = start, right = middle+1;for(int i= start; i<=end; i++) {if(left>middle) {//如果左边的首位下标大于中部下标,证明左边的数据已经排完了。data[i] = temp[right++];} else if(right>end) {//如果右边的首位下标大于了数组长度,证明右边的数据已经排完了。data[i] = temp[left++];} else if(temp[right]<temp[left]) {data[i] = temp[right++];//将右边的首位排入,然后右边的下标指针+1。}else {data[i]= temp[left++];//将右边的首位排入,然后右边的下标指针+1。}}}//6.快速排序:此处用递归实现,还可以考虑用栈操作替代递归实现<时间复杂度O(n*log(n)),空间复杂度O(log(n)),不稳定排序>public static void quickSort(int start, int end, int[] data) {if(start>= end) return;int p = partion(start,end,data);quickSort(start, p-1, data);quickSort(p+1,end,data);}//快速排序:双边扫描public static int partion(int start, int end, int[] data) {int left = start, right = end, p = data[start] ;while(left!=right) {while(data[right]>p&&left<right) {right--;}while(data[left]<=p&&left<right) {//”=“是为了保证排序算法的稳定性left++;}if(left<right) {int tmp = data[right];data[right] = data[left];data[left] = tmp;}}data[start] = data[left];data[left] = p;return left;}//7.堆排序<时间复杂度O(n*log(n)),空间复杂度O(1),不稳定排序>public static void heapSort(int[] data) {int len = data.length;//构建堆buildHeap(data, len);for(int i=len-1; i>0; i--) {int tmp = data[0];data[0] = data[i];data[i] = tmp;len--;sink(data, 0, len);}}//建堆private static void buildHeap(int[] data, int len) {for(int i=len/2; i>=0; i--) {sink(data, i, len);}}//调整:保证堆为大顶堆private static void sink(int[] data, int index, int len) {int leftChild = 2 * index + 1;//左子节点下标int rightChild = 2 * index + 2;//右子节点下标int current = index;//要调整的节点下标//下沉左边if (leftChild < len && data[leftChild] > data[current]) {current = leftChild;}//下沉右边if (rightChild < len && data[rightChild] > data[current]) {current = rightChild;}if(current!=index) {int tmp = data[index];data[index] = data[current];data[current] = tmp;//可能换下来的父节点比子节点小,所以继续下沉sink(data, current, len);}}///8.计数排序<时间复杂度O(n+k),空间复杂度O(n+k),稳定排序>public static void countSort(int[] data) {int len = data.length;int max=0, min=0;for(int i=0; i<len; i++) {if(max<data[i]) {max=data[i];}if(min>data[i]) {min=data[i];}}int countLen = max-min+1;int[] counts = new int[countLen];for(int i=0; i<len; i++) {counts[ data[i]-min ]++;}int index = 0;for(int i=0; i<countLen; i++) {while(counts[i]>0) {data[index++] = i+ min;counts[i]--;}}}//9.桶排序<时间复杂度O(n+k),空间复杂度O(n+k),稳定排序>public static void bucketSort(int[] data) {int len = data.length;int max=data[0],min=data[0];for(int i=0; i<len; i++) {if(max<data[i]) {max=data[i];}if(min>data[i]) {min=data[i];}}int gap = max - min;ArrayList<ArrayList<Integer>> buckets = new ArrayList<ArrayList<Integer>>();for(int i=0; i<len; i++) {buckets.add(new ArrayList<Integer>());}//每个桶大小,因为不一定会除尽,余下的全部放到最后一个桶中int bucketSize = (int) Math.ceil((float)gap/ len);if(bucketSize<1) bucketSize = 1;//数据入桶for(int i=0; i<len; i++) {int index = (data[i]-min)/bucketSize ;buckets.get(index).add(data[i]);}int index =0;for(int i=0; i<len; i++) {ArrayList<Integer> bucket = buckets.get(i);if(bucket!=null&&bucket.size()!=0) {Collections.sort(buckets.get(i));for(int value:bucket) {data[index++] = value;}}}}//10.基数排序<时间复杂度O(n+k),空间复杂度O(n+k),稳定排序>public static void radixSort(int[] data) {int len = data.length;int max=data[0];for(int i=0; i<len; i++) {if(max<data[i]) {max=data[i];}}ArrayList<ArrayList<Integer>> buckets = new ArrayList<ArrayList<Integer>>();for(int i=0; i<10; i++) {buckets.add(new ArrayList<Integer>());}int radix = 1;//底数,找到待排数的相应位while(true) {if(max<radix) {break;}//当最大的数比底数小,表示所有的位已经排完for(int i=0; i<len; i++) {int index = (data[i]/radix)%10;buckets.get(index).add(data[i]);}//将桶中的数写回int index = 0;for(int i=0; i<10; i++) {for(int value:buckets.get(i)) {data[index++] = value;}buckets.get(i).clear();}radix *= 10;}}public static void print(int[] data) {for(int i=0; i<data.length; i++) {System.out.print(data[i]+"\t");}System.out.println();}public static void main(String[] args) {int data[] = {912, 132, 182, 888, 218, 322, 511, 522, 533, 692,2, 22, 782,398, 999, 439 };//int data[] = {6,4,2,4,1,5};print(data);//bubbleSort(data);//selectSort(data);//insertSort(data);//hillSort(data);//mergeSort(data);//quickSort(0, data.length-1, data);heapSort(data);//countSort(data);//bucketSort(data);//radixSort(data);print(data);}
}
这篇关于图解、手撕十大排序算法[思路清晰版]的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





