本文主要是介绍数据的均匀化分割算法(网格划分法、四叉树法(含C++代码)),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
数据的均匀化分割主要是指在分割过程中尽可能均匀地将数据点分布在各个子区域中,以保持数据分布的平衡和优化数据结构的性能。以下是几种可以实现数据均匀化分割的方法:
一. 网格划分法
1. 基本概念
虽然传统的网格划分法不是动态调整的,但通过设计可以实现均匀的空间分割。例如,可以根据数据点的分布密度来调整网格的划分粒度,使得每个网格单元内包含的数据点数量尽量均匀。
具体的,二维网格划分是一种对二维空间进行均匀分割的技术,用于将这种空间划分为多个小的、有时是规则的区域或单元,称为“网格”或“格子”。在图像处理中,二维网格划分可以用于将图像划分成小块进行局部分析或并行处理,从而加速图像处理任务如滤波、特征检测等。

2. 示例
我有一组特征点存储在 std::vector<cv::KeyPoint> 类型的变量 vToDistributeKeys 中。这些特征点位于一张大小为宽1276像素、高378像素的图片上。为了在二维空间上实现点的均匀分布,我需要将图片分割成一个6x6的网格(共36个方块)。在每个方块内,我希望只保留具有最大置信度的特征点,并删除该方块内的其他点。下面是实现这一功能的具体C++代码。
#include <iostream>
#include <vector>
#include <opencv2/core/types.hpp>// 将特征点按网格均匀分布,每个网格只保留置信度最高的特征点
std::vector<cv::KeyPoint> distributeAndFilterKeys(const std::vector<cv::KeyPoint>& keypoints, int width, int height, int gridRows, int gridCols) {// 计算每个网格的尺寸int cellWidth = width / gridCols;int cellHeight = height / gridRows;// 初始化网格,用于存储每个网格的最高置信度的特征点std::vector<std::vector<cv::KeyPoint>> grid(gridRows, std::vector<cv::KeyPoint>(gridCols));// 遍历所有特征点for (const auto& keypoint : keypoints) {int gridX = keypoint.pt.x / cellWidth;int gridY = keypoint.pt.y / cellHeight;// 确保网格索引不越界if (gridX >= gridCols) gridX = gridCols - 1;if (gridY >= gridRows) gridY = gridRows - 1;// 检查当前网格是否已有特征点,或者当前特征点置信度是否更高if (!grid[gridY][gridX].empty() && grid[gridY][gridX][0].response < keypoint.response) {grid[gridY][gridX][0] = keypoint;} else if (grid[gridY][gridX].empty()) {grid[gridY][gridX].push_back(keypoint);}}// 收集所有网格中的最佳特征点std::vector<cv::KeyPoint> filteredKeyPoints;for (int y = 0; y < gridRows; ++y) {for (int x = 0; x < gridCols; ++x) {if (!grid[y][x].empty()) {filteredKeyPoints.push_back(grid[y][x][0]);}}}return filteredKeyPoints;
}int main() {// 假设的特征点数据std::vector<cv::KeyPoint> keypoints = {{cv::Point2f(100, 50), 1.f, -1, 0.8},{cv::Point2f(120, 60), 1.f, -1, 0.9},{cv::Point2f(130, 55), 1.f, -1, 0.95},// 添加更多点以测试};// 图片尺寸和网格配置int width = 1276;int height = 378;int gridRows = 6;int gridCols = 6;// 处理特征点std::vector<cv::KeyPoint> filteredKeyPoints = distributeAndFilterKeys(keypoints, width, height, gridRows, gridCols);// 输出结果for (const auto& kp : filteredKeyPoints) {std::cout << "Keypoint at (" << kp.pt.x << ", " << kp.pt.y << ") with response: " << kp.response << std::endl;}return 0;
}二. 四叉树均匀化与非极大值抑制结合使用
在实际应用中,可以先对ORB特征点进行四叉树均匀化,然后再对每个子区域内的特征点进行非极大值抑制。这样可以在保证特征点分布均匀性的同时,提高特征点的质量和稳定性,最终得到更优的特征点集合。
1. 四叉树的基本概念
在图像中,某些区域可能存在大量的特征点,而其他区域可能只有很少的特征点。这种不均匀分布会影响特征点的代表性和匹配效果。
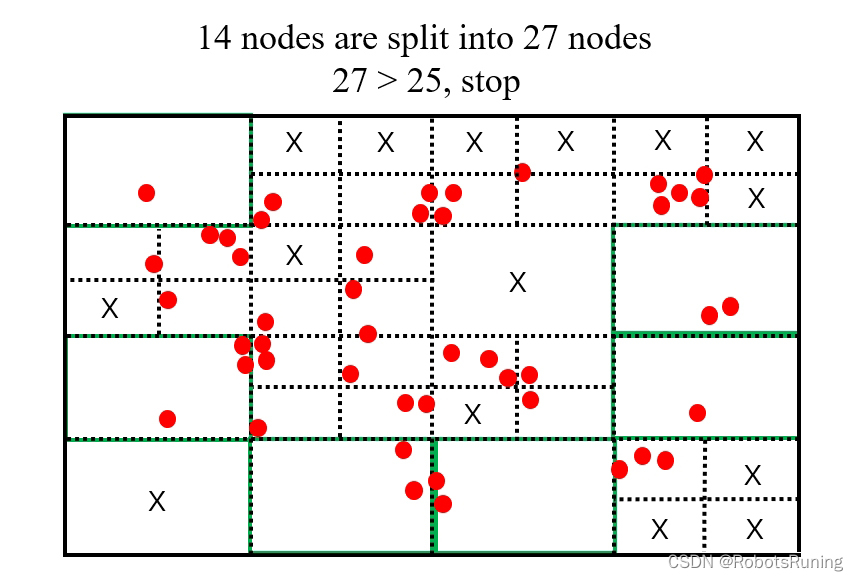
首先把一幅图案或一个幅面分割成多个分区或者部分。如果某个子区域内的特征点数量少于某个预设阈值,或者已经达到了分割的最小尺度,则这个子区域不再进行分割。如果特征点过于密集,则继续将这个区域分割成四个更小的子区域,并递归地对每个子区域进行同样的分割过程,直至每个子区域内的特征点数量满足预设条件。
通过控制划分的停止条件(如特征点数量少于阈值、达到最小分割尺寸等),可以在保证足够的特征点总数的同时,让特征点在图像的不同区域内尽可能均匀分布。
在划分完成后,每个子区域内可能包含多个特征点。为了进一步提高均匀性和代表性,可以在每个子区域内只保留响应值最大的特征点,去除其他的特征点。
2. 非极大值抑制
非极大值抑制是一种常用的特征点后处理方法,主要用于去除临近区域内响应值较低的特征点,保留局部最大的特征点。其基本原理是,对于每个特征点,检查其周围邻域内是否存在响应值更大的特征点。如果存在,则将当前特征点去除;如果不存在,则保留当前特征点。
3. 示例
一组特征点存储在 std::vector<cv::KeyPoint> 类型的变量 vToDistributeKeys 中。这些特征点分布在一张宽为1276像素、高为378像素的图片上。要求将图片分割成至少25个区域。
#include <opencv2/opencv.hpp>
#include <vector>
#include <algorithm>// 定义四叉树节点结构体
struct QuadTreeNode {cv::Rect rect; // 节点代表的区域std::vector<cv::KeyPoint> keypoints; // 节点内的特征点QuadTreeNode* children[4]; // 子节点指针QuadTreeNode(cv::Rect _rect) : rect(_rect) {for (int i = 0; i < 4; i++) {children[i] = nullptr;}}
};// 递归建立四叉树
void buildQuadTree(QuadTreeNode* node, const std::vector<cv::KeyPoint>& keypoints, int minPoints, int maxLevel, int level) {if (level >= maxLevel || node->keypoints.size() <= minPoints) {return;}// 将当前节点划分为四个子区域int halfWidth = node->rect.width / 2;int halfHeight = node->rect.height / 2;cv::Rect childRects[4] = {cv::Rect(node->rect.x, node->rect.y, halfWidth, halfHeight),cv::Rect(node->rect.x + halfWidth, node->rect.y, halfWidth, halfHeight),cv::Rect(node->rect.x, node->rect.y + halfHeight, halfWidth, halfHeight),cv::Rect(node->rect.x + halfWidth, node->rect.y + halfHeight, halfWidth, halfHeight)};// 为每个子区域创建子节点for (int i = 0; i < 4; i++) {node->children[i] = new QuadTreeNode(childRects[i]);}// 将特征点分配到子节点中for (const auto& keypoint : node->keypoints) {for (int i = 0; i < 4; i++) {if (node->children[i]->rect.contains(keypoint.pt)) {node->children[i]->keypoints.push_back(keypoint);break;}}}// 递归建立子节点的四叉树for (int i = 0; i < 4; i++) {buildQuadTree(node->children[i], node->children[i]->keypoints, minPoints, maxLevel, level + 1);}
}// 非极大值抑制
void nonMaximumSuppression(std::vector<cv::KeyPoint>& keypoints, float radius) {std::vector<cv::KeyPoint> nmsKeypoints;std::sort(keypoints.begin(), keypoints.end(), [](const cv::KeyPoint& a, const cv::KeyPoint& b) {return a.response > b.response;});std::vector<bool> mask(keypoints.size(), true);for (size_t i = 0; i < keypoints.size(); i++) {if (mask[i]) {nmsKeypoints.push_back(keypoints[i]);for (size_t j = i + 1; j < keypoints.size(); j++) {if (cv::norm(keypoints[i].pt - keypoints[j].pt) <= radius) {mask[j] = false;}}}}keypoints = nmsKeypoints;
}// 四叉树均匀化结合非极大值抑制
void quadTreeUniformNMS(std::vector<cv::KeyPoint>& keypoints, int minPoints, int maxLevel, float nmsRadius) {// 创建根节点QuadTreeNode* root = new QuadTreeNode(cv::Rect(0, 0, 1276, 378));root->keypoints = keypoints;// 建立四叉树buildQuadTree(root, keypoints, minPoints, maxLevel, 0);// 对每个叶子节点进行非极大值抑制std::vector<cv::KeyPoint> uniformKeypoints;std::function<void(QuadTreeNode*)> traverseQuadTree = [&](QuadTreeNode* node) {if (node->children[0] == nullptr) {nonMaximumSuppression(node->keypoints, nmsRadius);uniformKeypoints.insert(uniformKeypoints.end(), node->keypoints.begin(), node->keypoints.end());} else {for (int i = 0; i < 4; i++) {traverseQuadTree(node->children[i]);}}};traverseQuadTree(root);keypoints = uniformKeypoints;// 释放内存std::function<void(QuadTreeNode*)> deleteQuadTree = [&](QuadTreeNode* node) {if (node->children[0] != nullptr) {for (int i = 0; i < 4; i++) {deleteQuadTree(node->children[i]);delete node->children[i];}}};deleteQuadTree(root);delete root;
}int main() {std::vector<cv::KeyPoint> vToDistributeKeys;// ... 初始化 vToDistributeKeys ...int minPoints = 1; // 每个区域最少特征点数量int maxLevel = 5; // 最大分割层数float nmsRadius = 10.0f; // 非极大值抑制半径quadTreeUniformNMS(vToDistributeKeys, minPoints, maxLevel, nmsRadius);// ... 使用均匀化后的特征点 vToDistributeKeys ...return 0;
}这篇关于数据的均匀化分割算法(网格划分法、四叉树法(含C++代码))的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




