本文主要是介绍Peter算法小课堂—二叉堆(优先队列),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
课前小视频:(7 封私信 / 62 条消息) 看动画,学算法,C++实现建立二叉堆,优先队列和堆排序的基础 - 知乎 (zhihu.com)
二叉堆(优先队列)
大家想想,什么数据结构能做到插入(删除)一个数、询问最小(大)值、 删除最小(大)值,时间复杂度最小。答案是:二叉堆!
那么,我们介绍一下二叉堆。看下图。

堆的定义
int h[MAXN],n;//用数组模拟堆堆的插入
首先将元素x放到堆中的最后一个位置(即最底层最右边的位置),然后不断地把x往上调整,直到x调不动为止(即大于现在的父亲,或者x处于根节点)。
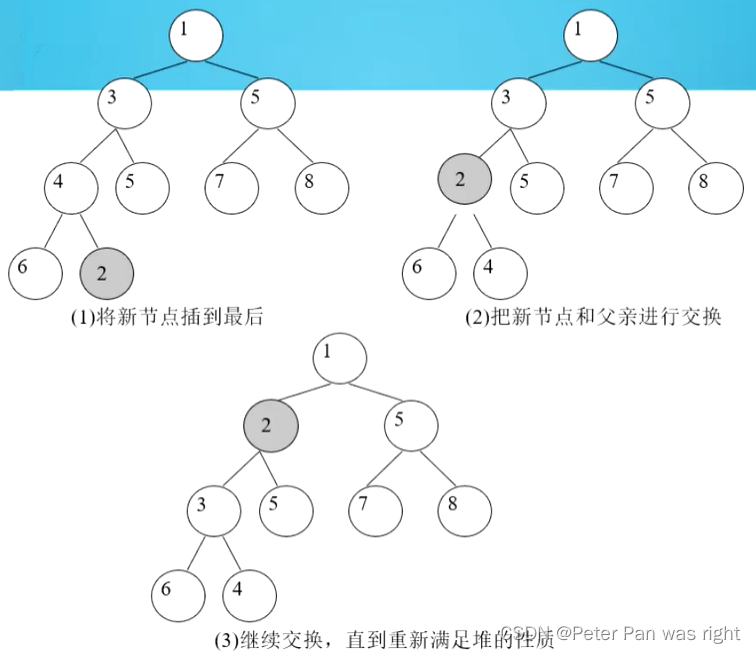
void up(int k){while(k>1){int i=k/2;if(h[k]<h[i]){swap(h[k],h[i]);k=i;}else break;}
}堆的删除
具体方法:

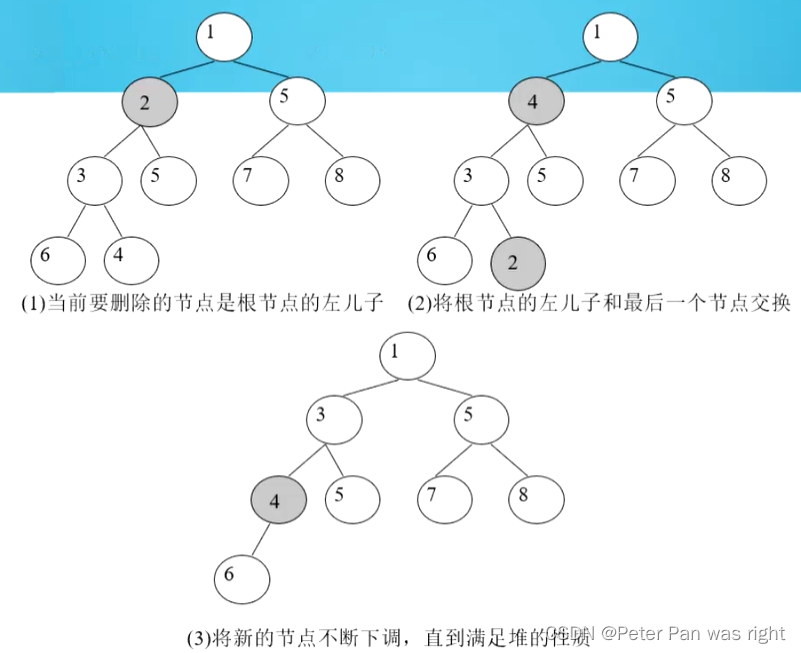
void down(int k){while(k+k<=n){int i=k+k;if(i+1<=n&&h[i+1]<h[i]) i++;if(h[i]<h[k]){swap(h[i],h[k]);k=i;}else break;}
}堆的插入/删除
void add(int x){++n;h[n]=x;up(n);
}
void del(int pos){swap(h[pos],h[n]);--n;up(pos);down(pos);
}STL
优先队列STL:
大根堆:priority_queue
小根堆:priority_queue(int ,vector(int),greater(int)) p;
用法:p.top();p.push();p.pop();p.size();p.empty();
题目
1.给定 n个整数,用要求的排序方法(堆排序、归并排序)进行从大到小的排序。
#include <bits/stdc++.h>
using namespace std;
int n,a[100009],b[100009],k=1;
priority_queue<int> p;
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];p.push(a[i]);}for(int i=1;i<=n;i++){int a=p.top();p.pop();b[k]=a;k++;}for(int i=1;i<=n;i++){cout<<b[i]<<endl;}return 0;
}2.
小明在玩一个数字游戏。游戏规则是这样的,一开始小明那里一个数字也没有,然后他会接受 2 种指令,根据这 2 种指令执行操作,并且回答其中的 q 指令。
2 种指令如下:
a X Y,表示增加一个数字 X,数字 X 的价值是 Y
q,查询目前最小的数字,并且把这个数字删除。如果存在多个数字相同的,删除价值最大的那个。
#include <bits/stdc++.h>
using namespace std;
int n,x,y;
char op[10];
typedef pair<int,int> pii;
priority_queue<pii,vector<pii>,greater<pii> > pq;
int main()
{scanf("%d",&n);while (n--) {scanf("%s",op);if (op[0]=='a') {scanf("%d%d",&x,&y);pq.push(make_pair(x,-y));} else {pii p=pq.top(); pq.pop();printf("%d %d\n",p.first,-p.second);}}return 0;
}3.有两个长度都是 N的序列 A 和 B,在 A 和 B 中各取一个数相加可以得到 N^2 个和,求这 N^2 个和中最小的 M个。
#include <bits/stdc++.h>
using namespace std;
struct A {int v,id;bool operator > (const A& a) const {return v>a.v;}
};
int n,m,a[100010],b[100010],c[100010];
priority_queue<A,vector<A>,greater<A> > pq;
int main() {scanf("%d%d",&n,&m);for (int i=1;i<=n;++i) scanf("%d",&a[i]);for (int i=1;i<=n;++i) scanf("%d",&b[i]);sort(b+1,b+1+n);for (int i=1;i<=n;++i) c[i]=1;for (int i=1;i<=n;i++) pq.push((A){a[i]+b[c[i]],i});for (int i=1,v,id;i<=m;i++) {v=pq.top().v; id=pq.top().id; pq.pop();printf("%d\n",v);if (++c[id]<=n)pq.push((A){a[id]+b[c[id]],id});}return 0;
}希望这些对大家有用,三连必回
这篇关于Peter算法小课堂—二叉堆(优先队列)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








