本文主要是介绍智能机器人与旋量代数(9),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Chapt 3. 螺旋运动与旋量代数
3.1 螺旋运动
螺旋运动是关于一条空间直线的一个旋转运动,并伴随沿此直线的一个平移。是一种刚体绕空间轴 s s s旋转 θ \theta θ角,再沿该轴平移距离 d d d的复合运动,类似螺母沿螺纹做进给运动的情形。
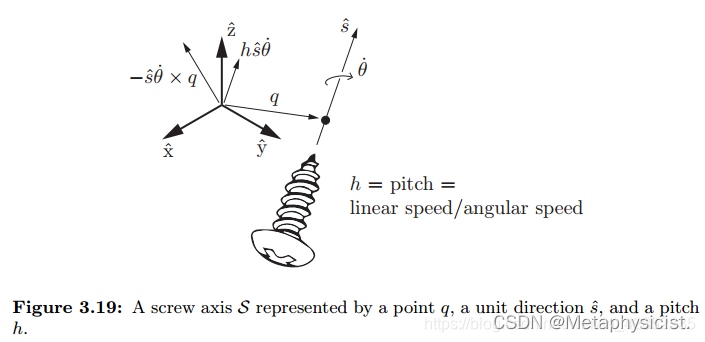
一些定义:
当 θ ≠ 0 \theta\neq0 θ=0 时,将移动量与转动量的比值 h = d θ h=\frac{d}{\theta} h=θd 定义为螺旋的节距(或螺距)。因此,旋转 θ \theta θ 角后的纯移动量为 h θ h\theta hθ。
当 h = 0 h=0 h=0 时为纯转动;当 h = ∞ ( θ = 0 ) h=\infin (\theta=0) h=∞(θ=0) 时为纯移动。
定义3.1 螺旋运动的三要素是:轴线 s s s、螺距 h h h和转角 ρ \rho ρ。螺旋运动表示绕轴 s s s旋转 ρ = θ \rho=\theta ρ=θ,再沿该轴平移距离 h θ h\theta hθ的合成运动。如果 h = ∞ h=\infin h=∞,那么相应的螺旋运动即为沿轴 s s s移动距离 ρ \rho ρ的移动,记作 S ( s , h , ρ ) S(s,h,\rho) S(s,h,ρ).
p ( θ , h ) = r + R ( θ , s ) ( p − r ) + h θ s , s ≠ 0 p(\theta,h)=r+R(\theta,s)(p-r)+h\theta s ,s\neq 0 p(θ,h)=r+R(θ,s)(p−r)+hθs,s=0
其中 R ( θ , s ) ∈ S O ( 3 ) R(\theta,s)\in SO(3) R(θ,s)∈SO(3)是关于空间某一条直线 s s s的刚体旋转运动。
表示成齐次坐标的形式为:
g ( p 1 ) = [ R ( I − R ) r + h θ s 0 1 ] ( p 1 ) g\begin{pmatrix} p\\ 1 \end{pmatrix}=\begin{bmatrix} R & (I-R)r+h\theta s \\ 0 & 1 \end{bmatrix}\begin{pmatrix} p\\ 1 \end{pmatrix} g(p1)=[R0(I−R)r+hθs1](p1)
由此可得,刚体螺旋运动的描述为:
[ R ( I − R ) r + h θ s 0 1 ] , s ≠ 0 \begin{bmatrix} R & (I-R)r+h\theta s \\ 0 & 1 \end{bmatrix},s\neq0 [R0(I−R)r+hθs1],s=0
Chasles-Mozzi定理(1830):任意刚体运动都可以通过螺旋运动即通过绕某轴的转动与沿该轴移动的负荷运动实现。即:刚体运动与螺旋运动等价,螺旋运动是刚体运动,刚体运动也是螺旋运动。螺旋运动的无限小量为运动旋量。
Chasles理论推广:对于任意的刚体运动总能将其表达为螺旋运动,满足如下关系式:
[ R P 0 1 ] = [ R ( θ , s ) h θ s + ( I 3 − R ) r 0 1 ] \begin{bmatrix} R & P\\ 0 & 1 \end{bmatrix}=\begin{bmatrix} R(\theta,s) &h \theta s+(I_3-R)r \\ 0 & 1 \end{bmatrix} [R0P1]=[R(θ,s)0hθs+(I3−R)r1]
更进一步,对于转动情况,定义矩阵指数与矩阵对数:
e x p : [ S ] θ ∈ s e ( 3 ) → T ∈ S E ( 3 ) . exp: [S]\theta\in se(3) \rightarrow T\in SE(3). exp:[S]θ∈se(3)→T∈SE(3).
l o g : T ∈ S E ( 3 ) → [ S ] θ ∈ s e ( 3 ) . log: T\in SE(3) \rightarrow [S]\theta\in se(3). log:T∈SE(3)→[S]θ∈se(3).
由Euler-Rodrigues formula 得如下命题:
令 S = ( ω , v ) S=(\omega,v) S=(ω,v)为螺旋轴,若 ∣ ∣ ω ∣ ∣ = 1 ||\omega||=1 ∣∣ω∣∣=1,则对于任意沿螺旋轴的距离 θ ∈ R \theta \in R θ∈R,都有
s [ S ] θ = [ e [ ω ] θ ( I θ + ( 1 − c o s θ ) [ ω ] + ( θ − s i n θ ) [ ω ] 2 ) v 0 1 ] s^{[S]\theta}=\begin{bmatrix} e^{[\omega]\theta} & (I\theta+(1-cos\theta)[\omega]+(\theta-sin\theta)[\omega]^2)v \\ 0 & 1 \end{bmatrix} s[S]θ=[e[ω]θ0(Iθ+(1−cosθ)[ω]+(θ−sinθ)[ω]2)v1]
Reference
[1] Lynch, K. M., & Park, F. C. (2017). Modern robotics. Cambridge University Press.
[2] Dai, J. S. (2014). Geometrical foundations and screw algebra for mechanisms and robotics. Higher Education Press, also Screw Algebra and Kinematic Approaches for Mechanisms and Robotics.
[3] Ding, X. L. (2021). Modern Mathematical Theory Foundation of Robotics. Beijing: Science Press.
[4] Gao, X. et al. (2017). Visual SLAM fourteen lessons: From theory to practice. Electronic Industry Press.
这篇关于智能机器人与旋量代数(9)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







