本文主要是介绍双指针算法: 快乐数 与 盛水最多的容器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
前言
声明:题目来源于: 力扣
一、快乐数
题目链接: 传送门
(1) 题目描述
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
返回值:
如果 n 是 快乐数 就返回 true ;
不是,则返回 false 。
示例:
示例 1:
输入:
n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
(2)解题思路
刚开始见到这道题的时候,毫无思路,知道会循环又如何?什么时候结束循环才麻烦。
我总不能每次循环都判断结果是否为1吧?计算是这样,那要是一直不为1咋办,死循环,也就死翘翘了。
快乐数,有点也不快乐!

总不能不做吧,我们不妨画图分析一下。
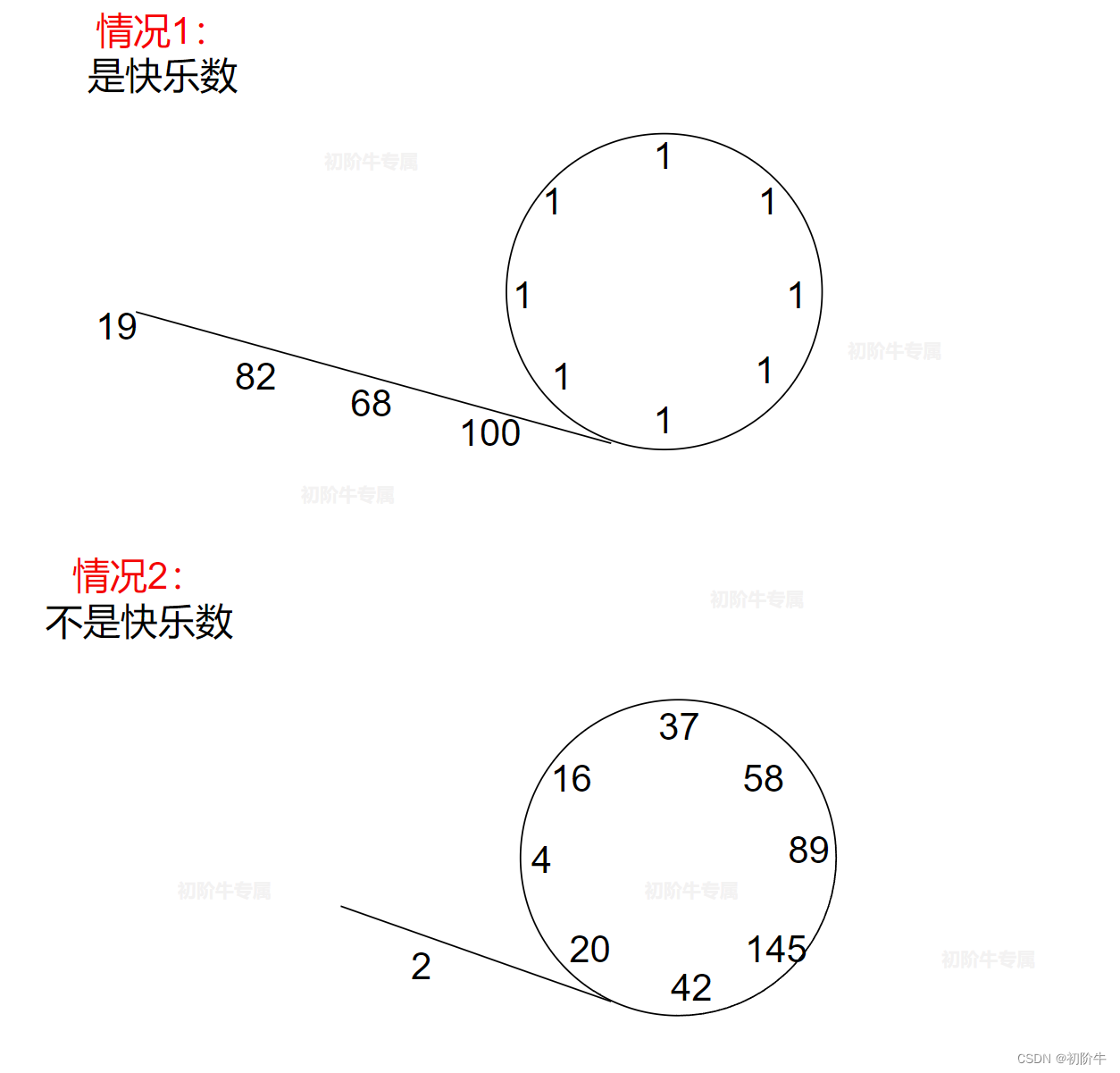
是不是有点眼熟,画完图以后,我们惊奇的发现,这好像与带环链表问题极其相似。
环形链表博客(第二题)
在环形链表II 中,我们向后一步是next指针往后遍历,本题是每一次将该数替换为它每个位置上的数字的平方和。
- 我们可以将 “求每个位数的平方和”封装成一个函数(
func)。 - 定义快慢指针:
快指针每次调用两次func函数。
慢指针每次调用一次func函数。 - 快慢指针相遇时,即为环的入口点。
- 入口点是
1,则为快乐数,返回ture;
入口点非1,则不是快乐数,返回false;
(3)代码展示:
class Solution {
public:bool isHappy(int n) {int slow=n;int fast=n;do{slow=func(slow);fast=func(func(fast));}while(slow!=fast);//跳出循环,此时快慢指针相遇if(slow!=1)return false;return true;}int func(int n){ //求每个位数的平方和int ret=0;while(n){int mod=n%10;ret+=(mod*mod);n/=10;}return ret;}
};
二、盛水最多的容器
(1) 题目描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
示例:
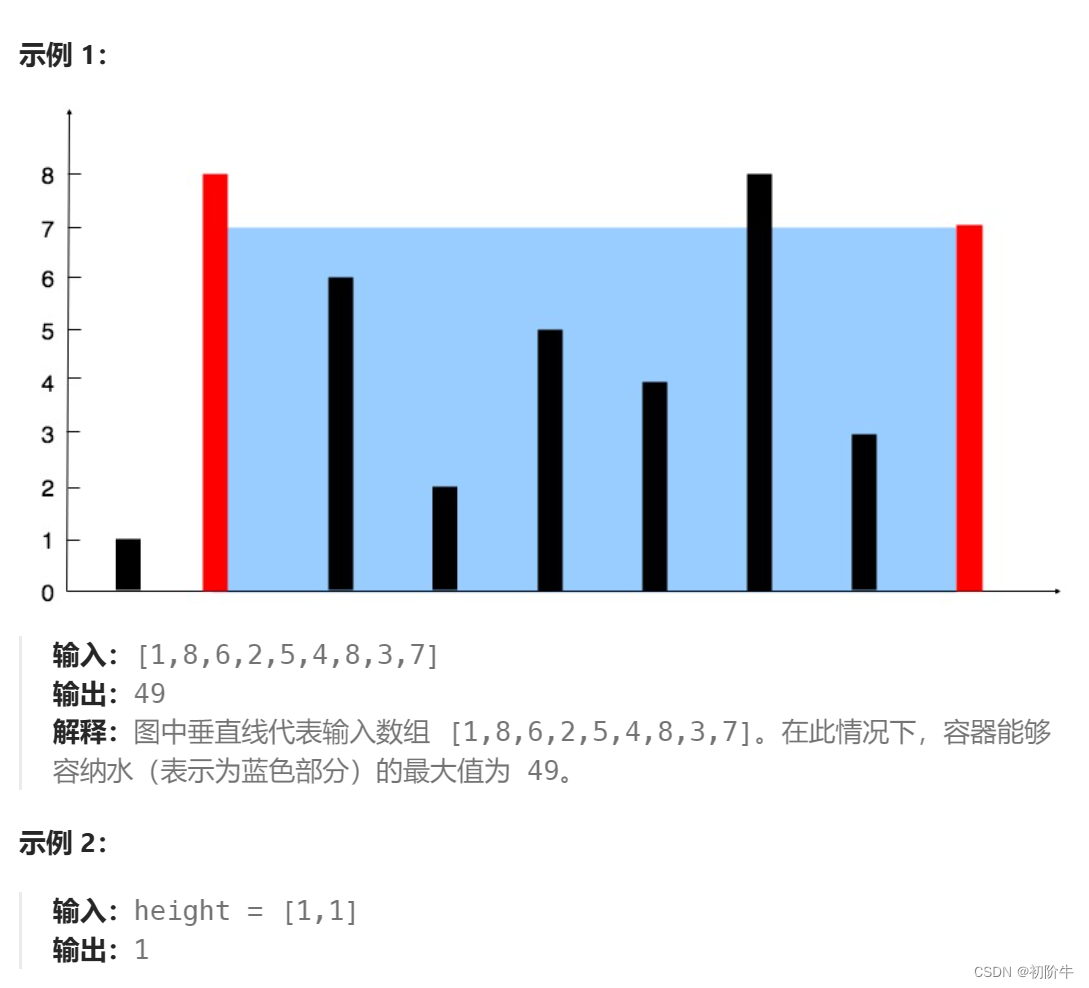
(2)解题思路
其实题目意思很简单,看图就很容易理解,就是寻找两个下标位置,将其最短的作为容器的高,两个坐标的距离作为容器的底,求出容积最大情况时,两个下标的位置。
- 定义两个指针:
(1)left最初位置
(2)right最后一个位置 - 先计算这边界状态时,容器的容量。
- 如果左边界比右边界高,则移动右边界。
如果我们移动左边界:
取到比右边界的值大: 则容器的高度依旧是右边界,低长度下降,总容量下降。
取到比右边界的值小,则容器的高度是左边界,这样的左边界只会让高度更低,而低的长度下降,总容量下降。
如果我们移动右边界:
取到比左边界的值大: 则容器的高度是左边界,高度会增加,虽然底的长度下降,但是容量可能上升。
取到比左边界的值小,则容器的高度是右边界,高度更低,低的长度下降,总容量下降。
-
如果右边界比左边界高,则移动左边界。
同理,这里就不再分析了。 -
计算移动后的容量,并判断是否需要更新容量。
(3)代码展示:
class Solution {
public:int maxArea(vector<int>& height) {int left=0,right=height.size()-1;//边界时的面积int maxv=(right-left)* min(height[left], height[right]);while(left<right){//如果左边界比右边界高,则移动右边界if(height[left]>height[right]) --right;else ++left;//计算移动边界以后的面积int v=(right-left)*min(height[left],height[right]);//取最大面积maxv=max(maxv,v);}return maxv;}
};
这篇关于双指针算法: 快乐数 与 盛水最多的容器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







