用于全局复根和极点查找算法的自适应网格生成器（Matlab代码实现）

本文主要是介绍用于全局复根和极点查找算法的自适应网格生成器（Matlab代码实现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果编辑

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

SA-GRPF算法旨在找到固定区域中函数的所有零点和极点。该程序包括一种为常规GRPF算法创建自适应初始网格的方法。所提出的解决方案使用梯度计算来确定需要细化的网格区域，包括零点和极点接近的区域。可以分析一类函数，并且可以考虑任意形状的搜索区域。如所附示例所示，自适应网格允许使用更少的样本更快、更准确地分析函数。该算法不仅限于计算电动力学。它可用于类似的问题，例如声学、控制理论和量子力学。

文件简介：

SA_GRPF.m - 启动程序
analysis_parameters.m - 包含分析的所有参数，例如：

矩形域大小（XB，XE，YB，YE)
精度
方法：两个可用的自适应和常规GRPF - （模式)
可选趣味参数（可选）)
缓冲区（ItMax， NodesMin， NodesMax)

fun.m - 计算根和极的函数的定义
运行示例：在 SA_GRPF.m （addpath）中添加文件夹取消注释行 23 或 24，以便包含包含（analysis_parameters.m）和（fun.m）文件的文件夹，或将它们从包含示例的文件夹复制到主文件夹并启动 SA_GRPF 程序。

自适应网格生成器是一种用于优化算法的工具，可以帮助在复杂的问题空间中进行搜索。在全局复根和极点查找算法中，自适应网格生成器可以用来帮助确定算法在复杂函数中查找根和极点的位置。以下是一个自适应网格生成器的工作流程，适用于全局复根和极点查找算法：

初始网格生成：确定搜索空间的初始边界和分辨率。这可以是一个较大的矩形区域，或者是函数定义域的一部分。选择初始网格的分辨率，即在每个维度上分割区间的数量。

函数评估：在初始网格中的每个网格点处评估函数的值。根据函数值的正负性，可以确定是否可能存在根或极点。

网格点分析：分析网格点处的函数值，尤其是找到可能的根和极点。这可以通过观察函数值的符号变化、斜率变化等来实现。

细分网格：对于在前一步中找到的可能的根和极点，可以选择在其周围细分网格以进一步精细搜索。这可以是固定的细分因子，或者可以根据函数的性质自适应地确定。

迭代：重复执行步骤 3 和步骤 4，直到达到预定的迭代次数或满足一定的收敛条件。每次迭代都会根据当前网格的情况进行进一步的网格细化。

结果提取：在最终的网格中，可以确定函数的根和极点的位置。这可以通过分析细分网格中的函数值和性质来完成。

收敛性判断：在算法运行过程中，可以监控根和极点的位置是否收敛到某个稳定状态。如果在连续的迭代中，根和极点的位置变化很小，可以认为算法已经收敛。

📚2 运行结果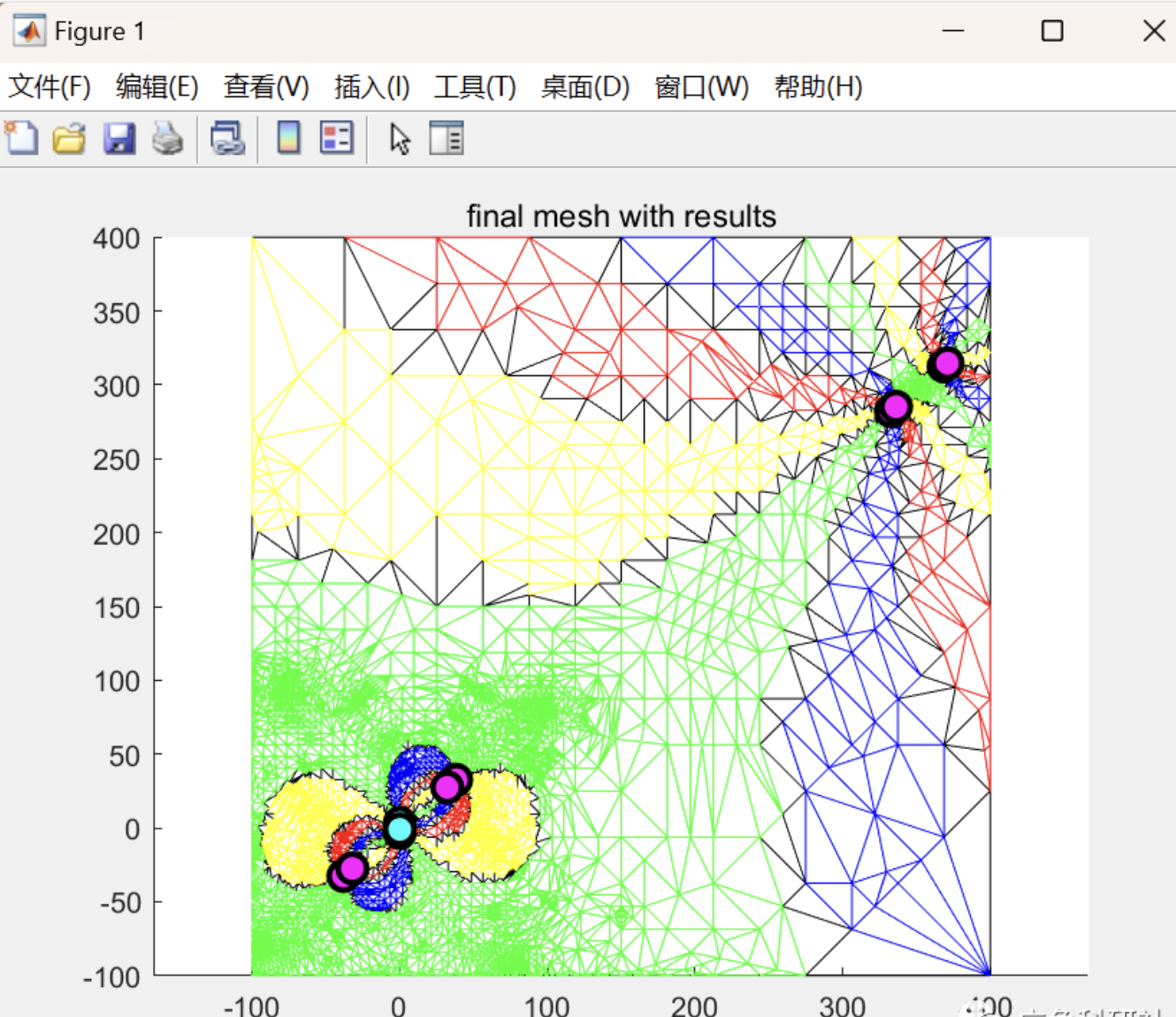

主函数部分代码：

close all;
clear all;
clc;
format long;
restoredefaultpath

%choose the example
%addpath('0_rational_function');
addpath('3_graphene_transmission_line');

analysis_parameters %input file
NewNodesCoord = rect_dom(xb,xe,yb,ye); %generates the initial mesh

%initialization of the variables
it=0;
NodesCoord=[];
PreviousIt.EdgesToSplit=[];
PreviousIt.Elements=[];
PreviousIt.GradeInElements=[];
NrOfNodes = size(NodesCoord,1);

%%%% analysis modes    
%Mode = 0 - Self-adaptive Mesh Generator 
%Mode = 1 - Regular Global complex Roots and Poles Finding algorithm -> https://github.com/PioKow/GRPF
%Mode = 2 - The result of aborted analysis
%Mode = 3 - The final result (accuracy achieved)
%%%%
%% general loop
while it<ItMax && Mode<2
%function evaluationNodesCoord=[NodesCoord ; NewNodesCoord];disp(['Evaluation of the function in ',num2str(size(NewNodesCoord,1)),' new points...'])
TimerOfFunEval = tic;for Node=NrOfNodes+1:NrOfNodes+size(NewNodesCoord,1)FunctionValues(Node,1)=fun(NodesCoord(Node,:),Optional);Quadrants(Node,1) = vinq( FunctionValues(Node,1) );endif(size(NewNodesCoord,1)>0)SingleNodeTime = toc(TimerOfFunEval)/size(NewNodesCoord,1);elseSingleNodeTime=NaN;end
%%% meshing operationNrOfNodes=size(NodesCoord,1);disp(['Triangulation and analysis of ',num2str(NrOfNodes),' nodes...'])DT = delaunayTriangulation(NodesCoord(:,1),NodesCoord(:,2));Elements = DT.ConnectivityList;Edges = edges(DT);
%phase analysisPhasesDiff=abs(Quadrants(Edges(:,1))-Quadrants(Edges(:,2)));PhasesDiff(PhasesDiff==3)=1;CandidateEdges=Edges(PhasesDiff==2|isnan(PhasesDiff),:);
%Self-adaptive Mesh Generator Modeif(Mode==0)[EdgesToSplit,GradeInElements] = adaptive(NodesCoord,FunctionValues,DT,Elements,Edges,CandidateEdges,PreviousIt,Tol);PreviousIt.EdgesToSplit=EdgesToSplit;PreviousIt.Elements=Elements;PreviousIt.GradeInElements=GradeInElements;
if(isempty(EdgesToSplit))Mode = 3;elseif(NrOfNodes>NodesMin && NrOfNodes<NodesMax)%visualizationvis(NodesCoord, Edges, Quadrants,PhasesDiff)disp(['Do you want to continue the SA mode and add new ',num2str(size(EdgesToSplit,1)),' points?'])disp(['Estimated time of the analysis: ',num2str(floor(size(EdgesToSplit,1)*SingleNodeTime)),' s'])Mode=-1;while Mode<0Prompt = 'Select analysis mode -> Adaptive/Regular/Cancel? [a]/[r]/[c]';str = input(Prompt,'s');if(str=="r")Mode=1;elseif(str=="c")Mode=2;elseif(str=="a")Mode=0;endendelseif(NrOfNodes>=NodesMax)Mode = 1;endif(Mode==1)disp("The mode has been switched to the regular GRPF")disp('---------------------')endend
if(Mode==1) %Regular Global complex Roots and Poles Finding algorithm[EdgesToSplit, Mode] = regular(NodesCoord,Tol,DT,Elements,CandidateEdges);end