日练算法-单词拆分

本文主要是介绍日练算法-单词拆分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 题目

1.1 题目描述

给你一个字符串 str 和一个字符串列表 wordDict 作为字典。
请你判断是否可以利用字典中出现的单词拼接出 str 。原题链接：https://leetcode-cn.com/problems/word-break/

解题注意：

1.拆分时可以重复使用字典中的单词，可以假设字典中没有重复的单词；
2.不要求字典中出现的单词都被使用

示例

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。

注意，你可以重复使用字典中的单词

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

1.2 题目分析及解答

解题思路1-遍历

解答该题同样可以使用暴力的遍历方式，只是这两种遍历较之前有些变化。如下：

1.深度优先遍历搜索(DFS)
2.广度优先遍历搜索(BFS)

DFS方法

首先，针对深度遍历搜索方法，其定义为：是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索（百度百科）。具体思路如下图：

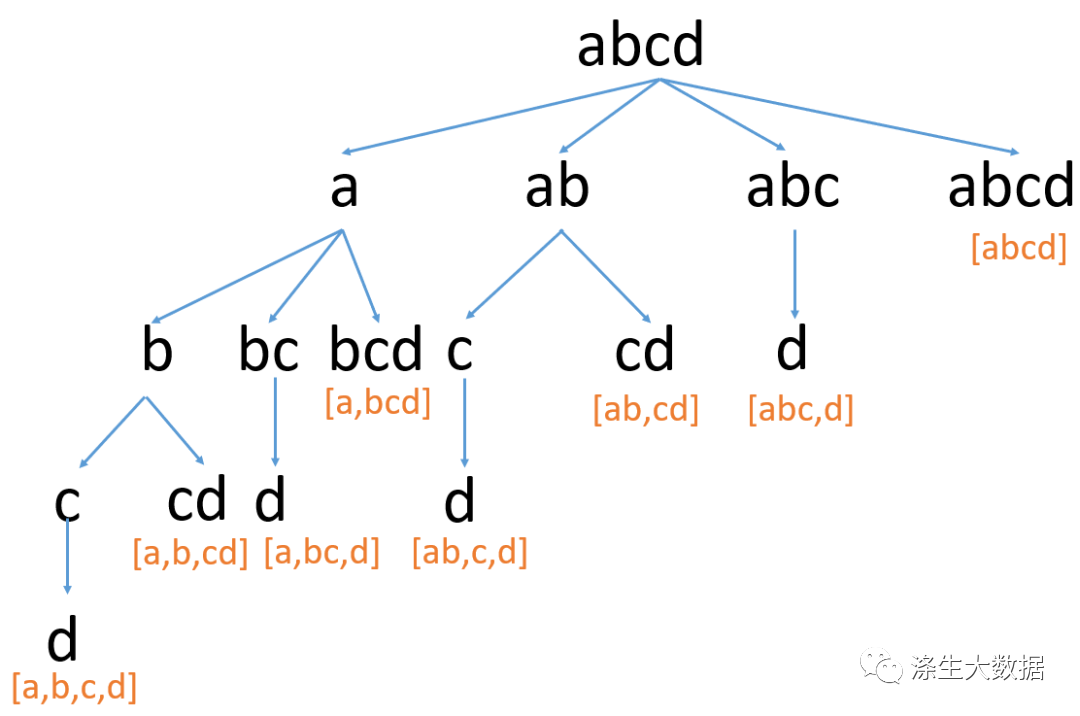
思路：每次截取一个子串，判断他是否存在于字典中，如果不存在于字典中，继续截取更长的子串……如果存在于字典中，然后递归拆分剩下的子串，这是一个递归的过程。上面的执行过程我们可以把它看做是一棵n叉树的DFS遍历

package list;
import java.util.Arrays;
import java.util.HashSet;
import java.util.List;
import java.util.Set;public class IDEA_1 {public static void main(String[] args){//数组可以随机定义，此处选取LeetCode数据String str = "leetcode";List<String> wordDict = Arrays.asList("leet", "code");System.out.println("单词拆分结果："+ wordBreak(str,wordDict));}public static boolean wordBreak(String s, List<String> wordDict) {return dfs(s, wordDict, new HashSet<>(), 0);}//start表示的是从字符串s的哪个位置开始public static boolean dfs(String s, List<String> wordDict, Set<Integer> indexSet, int start) {//字符串都拆分完了，返回trueif (start == s.length())return true;for (int i = start + 1; i <= s.length(); i++) {//如果已经判断过了，就直接跳过，防止重复判断if (indexSet.contains(i))continue;//截取子串，判断是否是在字典中if (wordDict.contains(s.substring(start, i))) {if (dfs(s, wordDict, indexSet, i))return true;//标记为已判断过indexSet.add(i);}}return false;}
}

BFS

对于BFS遍历算法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。如下图

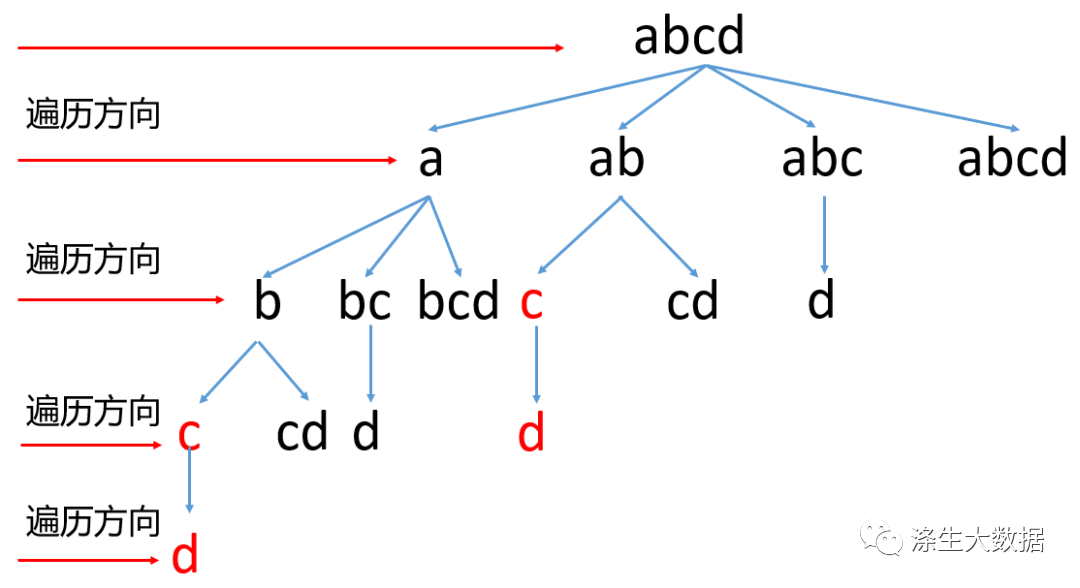
BFS算法只需要使用一个队列记录每一层需要记录的值即可。BFS中在截取的时候，如果截取的子串存在于字典中，我们就要记录截取的位置，到下一层的时候就从这个位置的下一个继续截取，代码如下：

package list;
import java.util.*;public class IDEA_2 {public static void main(String[] args){//数组可以随机定义，此处选取LeetCode数据String str = "leetcode";List<String> wordDict = Arrays.asList("leet", "code");System.out.println("单词拆分结果："+ wordBreak(str,wordDict));}public static boolean wordBreak(String s, List<String> wordDict) {//这里为了提高效率，把list转化为set，因为set的查找效率要比list高Set<String> setDict = new HashSet<>(wordDict);//记录当前层开始遍历字符串s的位置Queue<Integer> queue = new LinkedList<>();queue.add(0);int length = s.length();//记录访问过的位置，减少重复判断boolean[] visited = new boolean[length];while (!queue.isEmpty()) {int index = queue.poll();//如果字符串都遍历完了，直接返回trueif (index == length)return true;//如果被访问过，则跳过if (visited[index])continue;//标记为访问过visited[index] = true;for (int i = index + 1; i <= length; i++) {if (setDict.contains(s.substring(index, i))) {queue.add(i);}}}return false;}
}

以上两种方法可以解决问题，但是执行效率较低，leetcode和牛客等网站编译不易通过。

解题思路2-动态规划

1、确定dp数组以及下标的含义——这里dp[i]：字符串长度为i，dp[i]=true表示可以拆分为一个或多个在字典中出现的单词
2、确定递推公式，if(dp[j]=true && set.contains(s.substring(j,i))，才会出现dp[i]=true
3、dp数组初始化,dp[0]=true
4、确定遍历顺序，双层for循环遍历，i从0到s.length（遍历所有字符串长度），j从长度0到i
5、举例推导dp数组
6、最后返回dp[s.length()]

我们定义dp[i]表示字符串的前i个字符经过拆分是否都存在于字典wordDict中。如果要求dp[i]，我们需要往前截取k个字符，判断子串[i-k+1，i]是否存在于字典wordDict中，并且前面[0，i-k]子串拆分的子串也是否都存在于wordDict中，如下图所示：

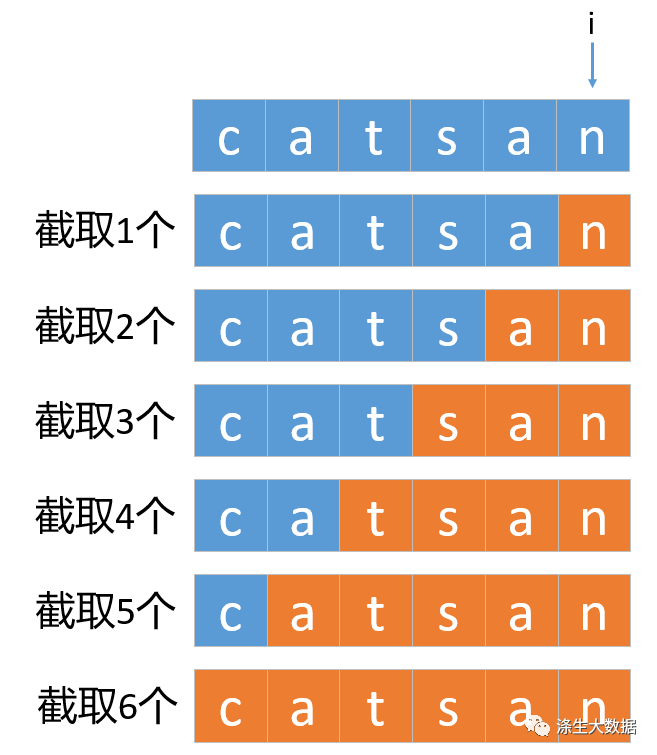
前面 [0，i-k] 子串拆分的子串是否都存在于 wordDict 中只需要判断 dp[i-k] 即可，而子串 [i-k+1，i] 是否存在于字典 wordDict 中需要查找，所以动态规划的递推公式很容易列出来

dp[i]=dp[i-k]&&dict.contains(s.substring(i-k, i));

package list;
import java.util.Arrays;
import java.util.List;public class IDEA_3 {public static void main(String[] args){//数组可以随机定义，此处选取LeetCode数据String str = "leetcode";List<String> wordDict = Arrays.asList("leet", "code");System.out.println("单词拆分结果："+ wordBreak(str,wordDict));}/**1.定义：boolean dp[i] -> 用字典中的单词能否前i个字符串2.递推公式：i > j如果前j个字符串能够用字典中的词汇拼出(这是前提) && 从j到i这段字符串能够在字典中找到 -> 说明前i个字符串能够用字典中的词汇拼出if(dp[j] == true && wordDict.contains(s.substring(j,i))) -> dp[i] = true 3.初始化：dp[0] = true 空字符串不用字典中的词汇也能拼出 无为而治 同时之后的结果也是以dp[0]为基础 如果为false之后的结果也都会为false4.遍历顺序：这道题理论上先遍历字符串(背包)还是先遍历字典(物品)的结果都是一样的只不过因为涉及到子串问题的特殊性 单词的顺序会进行打乱 不会按照字典中的顺序出现因此为了方便可以使用先遍历背包再遍历物品的方式如果反过来的话 需要先用容器将物品进行存储 较为麻烦*/public static boolean wordBreak(String s, List<String> dict) {boolean[] dp = new boolean[s.length() + 1];for (int i = 1; i <= s.length(); i++) {//枚举k的值for (int k = 0; k <= i; k++) {//如果往前截取全部字符串，我们直接判断子串[0,i-1]//是否存在于字典wordDict中即可if (k == i) {if (dict.contains(s.substring(0, i))) {dp[i] = true;continue;}}//递推公式dp[i] = dp[i - k] && dict.contains(s.substring(i - k, i));//如果dp[i]为true，说明前i个字符串结果拆解可以让他的所有子串//都存在于字典wordDict中，直接终止内层循环，不用再计算dp[i]了。if (dp[i]) {break;}}}return dp[s.length()];}}

正在上传…重新上传取消

优化： 将 wordDict 构建为一个 Set 能提高 contains 方法的匹配效率，于是：

package list;
import java.util.Arrays;
import java.util.HashSet;
import java.util.List;
import java.util.Set;public class IDEA_4 {public static void main(String[] args){//数组可以随机定义，此处选取LeetCode数据String str = "leetcode";List<String> wordDict = Arrays.asList("leet", "code");System.out.println("单词拆分结果："+ wordBreak(str,wordDict));}public static boolean wordBreak(String s, List<String> wordDict) {boolean[] dp = new boolean[s.length() + 1];dp[0] = true;//优化之处Set<String> set = new HashSet<>(wordDict);for (int r = 1; r < s.length() + 1; r++) {for (int l = 0; l < r; l++) {if (dp[l] == true && set.contains(s.substring(l, r))) {dp[r] = true;}}}return dp[s.length()];}

还有大佬优化的方法，此处给出代码逻辑，供大家思考：

public boolean wordBreak(String s, List<String> wordDict) {//转化为是否可以用 wordDict 中的词组合成 s，完全背包问题//有顺序的完全背包问题，先遍历target，再遍历背包//dp[i]表示：字符串的前i个字符是否可以由背包中的单词组成int len = s.length();boolean[] dp = new boolean[len + 1];//初始化ddp[0] = true;// 如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。// 所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。//这里从1开始遍历是因为substring左开右闭for(int i = 1; i <= len; i++){//倒着遍历，考虑到单词长度可能远小于target长度，倒着遍历效率更高for(int j = i - 1; j >= 0; j--){//如果dp[j]为false，已经不符合题意了，继续下一个比较if(dp[j] == false) continue;if(wordDict.contains(s.substring(j, i)) && dp[j]){//如果为true，则必定为true，直接breakdp[i] = true;break;}} }return dp[len];
}