本文主要是介绍(3.1)递归与分支之递归,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1.递归的定义
- 2.递归的基本思想
- 3.应用eg
- 4.递归与尾递归(非递归形式)
1.递归的定义
- 递归:
子程序(或函数) 直接调用自己或通过一系列调用语句间接调用自己,称为递归。
递归是一种描述问题和解决问题的基本方法。 - eg:函数A中的语句直接调用了函数A本身,这叫做直接递归调用。
void A()
{ …A();…
}
- eg:间接递归调用
void B()
{...C();...
}void C()
{...B();...
}
2.递归的基本思想
- 问题分解
- 递归的要素:
⑴ 递归边界条件:确定递归到何时终止,也称为递归出口;
⑵ 递归模式:大问题是如何分解为小问题的,也称为递归体。
3.应用eg
- eg:阶乘函数

递归算法
int fact ( int n )
{if ( n == 0 ) //边界条件return 1;else return n * fact (n-1);//递推关系式
}
-
求解阶乘 n! 的过程

-
递归过程与递归工作栈
(1)递归过程在实现时,需要自己调用自己。
(2)层层向下递归,返回次序正好相反:
(3)通过栈知道,函数调用就是通过栈来返回地址和参数传递的过程,因为他参数传递是用地址保存的;
递归也是通过栈来实现参数传递和他的解的值的传递

-
eg:使用非递归算法
能不用递归,就不用递归;
利用栈来实现非递归的算法,来提高效率;
不少递归问题就是尾递归,可以不借助栈,直接改成循环,效率高些;
写成递归形式,就是好看,容易理解;
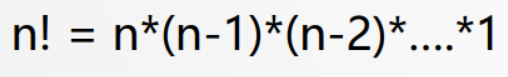
非递归算法
int fact ( int n )
{int f=n;while(--n>=1)//循环实现递归调用,避免使用递归,这里就是尾递归的方式f*=n;return f;
}
4.递归与尾递归(非递归形式)
- eg1:Fibonacci数列求解.

递归求解:
int f (int n)
{if (n<=1)return (n);elsereturn (f(n-1)+f(n-2));//递归关系式是作为return返回的,所以他是尾递归,所以可以改成循环语句,
}非递归求解,即:尾递归
int f(int n)
{ //pre:前一次Fibc的值;//now:现在Fibc的值;//next:下一次Fibc的值;int pre, now, next, j;if (n<=1) return (n);else{ pre=0;now=1;for(j=2;j<=n;j++){ next=pre+now;pre=now;now=next;}return(next);//j=n时,就是最终的解,直接return}
}
- eg2:回文串
如果一个字符串从左向右读和从右向左读完全相同 (不区分大小写),则这个字符串称为回文串(palindrome),例如“noon” 、“madam” 等都是回文串。
(1)递归思路

(2)非递归思路,即尾递归思路

递归方法:
bool palindrome(string &s,unsigned h,unsigned t)//h:字符串的起始地址,t:字符串的结束地址
{if (h>=t) //S是空串或长度为1return 1;if(tolower(s[h])==tolower(s[t]))//tolower都转换成小写return palindrome(s,h+1,t-1);//这里递归关系只在return的时候存在,也就是说这是尾递归,可以改成循环elsereturn 0;//返回是不是回文串
}
尾递归方法:
bool palindrome(string &s)
{int h=0,t=strlen(s)-1;while (h<=t){if (totlower(s[h])!=tolower(s[t]))return 0;else{h++;t--;}}return 1;
}这篇关于(3.1)递归与分支之递归的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





