激光SLAM入门笔记(二):轮式里程计模型及标定

本文主要是介绍激光SLAM入门笔记(二):轮式里程计模型及标定，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

内容基于深蓝学院课件，如有错误，烦请斧正，不胜感激。

1.模型

1.1 两轮差分底盘的运动学模型（以下简称运动模型）

1.1.1 目的

通过已知量推出未知量。

已知量

两轮角速度：$w_L,w_R$
两轮线速度：$v_L,v_R$
轮子离底盘中心的距离：$d$
两轮之间的距离：$b=2d$

未知量

底盘中心的线速度：$v$
底盘中心的角速度：$w$
底盘中心圆弧运动的半径：$r$

图

1.1.2 推导

首先明确，左右轮子的角速度是相同的，即
$$\begin{gathered} w_L=w_R \\ w=w_l=w_r \end{gathered}$$
其次明确，线速度是沟通大圆周（整个运动模型转圈）和小圆周（轮子转圈）的桥梁，即
$$\begin{gathered} v_L=w_l\ast (r-d)=w_L\ast r_L \\ {v}_R=w_r\ast (r+d)=w_R\ast r_R \end{gathered}$$

$r$

$w$

$v$

向量表示

1.2 航迹推算

递推公式

图

2.标定

2.1 线性最小二乘的基本原理

2.1.1 基础知识

线性方程组

$$Ax=b$$
其中，$A$为$m\ast n$的矩阵，$x$为$n\ast 1$的向量。
$m$表示约束个数，$n$表示自变量个数。

• 当$m=n$时，适定方程组，方程组有唯一解
• 当$m<n$时，欠定方程组，方程组有无穷多解
• 当$m>n$时，超定方程组，方程组通常无解

最小二乘解

• 绝大多数情况为$m>n$，超定方程组
• 多数约束自相矛盾，无解！
• 无解但有最小二乘解
• 通解:$x^{\ast }=(A^{T}A{)}^{-1}{A}^{T}b$
  下面会推导通解是怎么来的。

2.1.2 最小二乘求解

从线性空间的角度看最小二乘求解。

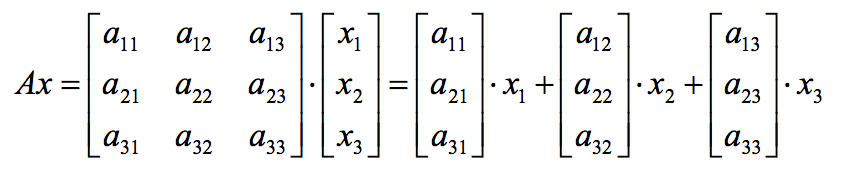
$S$表示$A$的列向量张成的线性空间。

• 无解：表示$Ax=b$对于任意的$x$均不成立，即$b$不在$S$中
• 最小二乘解：线性空间$S$中，离$b$最近的向量

设：$A{x}^{\ast }$为向量$b$在空间$S$中的投影，显然$(b-A{x}^{\ast })$垂直于空间$S$。
则：$(b-A{x}^{\ast })$跟矩阵A中的每一个列向量都垂直。
令$A=[a_1,a_2,\dots \dots ,a_n],a_i$表示矩阵$A$的第$i$个列向量，
可得

2.2 线性最小二乘的直线拟合

直线拟合

2.3 线性最小二乘在里程计标定中的应用

2.3.1 直接线性方法（通用、黑盒）

2.3.2 基于模型的方法（定制、白盒）

根据运动模型有

里程计的积分如下

假设

假设在标定的$\Delta t$时间内匀速运动，则
$$\begin{gathered} w(t)=w=J_{21}{w}_L+J_{22}{w}_R \\ v(t)=v=J_{11}{w}_L+J_{12}{w}_R \end{gathered}$$
因为$J_{11}=-\frac{b}{2}\ast J_{21},J_{12}=\frac{b}{2}\ast J_{22}$，
所以$v(t)=v=\frac{b}{2}(-J_{21}{w}_L+J_{22}{w}_R)$。
因此，已知量$w_L,w_R$，未知量$b,r_L,r_R,v$。
未知量求解顺序$b$→$r_L,r_R$→$v$。
假设

• 激光雷达位于车体的正中心
• 激光雷达的匹配值作为观测值
• 里程计的积分值作为预测值

通过最小化预测值和观测值的差，即可得到里程计的参数。

符号及推导

符号

• 里程计的积分值：$r_x,r_y,r_{\theta }$
• 激光雷达的匹配值：$S_x,S_y,S_{\theta }$

推导

（$\theta (t)$为运动模型在时刻$t$与世界坐标系$x$轴的夹角）

总结

收集$n$段数据，每段数据包含两个轮子的角速度$w_L$和$w_R$，该段数据持续的时间为$\Delta t$以及激光雷达的匹配值为$S_x,S_y,S_{\theta }$。

1. 按照公式1，计算中间变量$J_{21}$和$J_{22}$
2. 按照公式2，计算轮间距$b$
3. 按照公式3，计算两个轮子的半径$r_L,r_R$

这篇关于激光SLAM入门笔记(二):轮式里程计模型及标定的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---