算法学习012-不同路径 c++动态规划算法实现 中小学算法思维学习 信奥算法解析

本文主要是介绍算法学习012-不同路径 c++动态规划算法实现 中小学算法思维学习 信奥算法解析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

C++不同路径

一、题目要求

1、编程实现

2、输入输出

二、算法分析

三、程序编写

四、运行结果

五、考点分析

六、推荐资料

---

C++不同路径

一、题目要求

1、编程实现

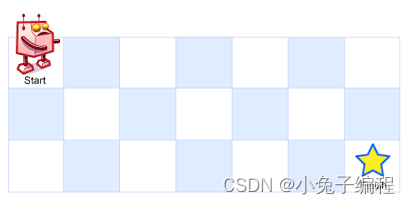
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

注：总的台阶数n在1到40之间

2、输入输出

输入描述：输入网络行列数m,n（1<=m,n<=100）

输出描述：只有一行，一个整数，即从开始到结束有多少条不同路径

输入样例：

3 728

输出样例：

7

二、算法分析

1. 从给定题目的初步分析可以看出，本题是问有多少种不同的路径可以到达
2. 而且题目已经规定只能是向左和向下走，实现的方法有多种
3. 这里采用动态规划的方式实现
4. 可以设置动态数组dp[i][j]，i和j表示对应网络的行和列号；所以对应的dp[i][j]就是从起始位置到达第i行和第j列所在网络有多少种方法
5. 而能够到达第i行j列所在网格有两种方法：一种是从上一行往下走到达，即第i-1行j列到达，对应的路径数就是dp[i-1][j]；另一种就是从左一列往右走到达，即第i行j-1列到达，对应的路径数就是dp[i][j-1]
6. 所以可以得出对应的动态数组dp[i][j]的状态转移方为：dp[i][j]=dp[i-1][j]+dp[i][j-1]
7. 而由于每一个网格都是从上或者从左到达的，所以初始的时候需要将第一行和第一列进行初始化，而第一行的值和第一列的值应该都是只有一种方法到达，所以都是1

三、程序编写

//程序中的dp和cost数组可以使用动态数组vector进行实现更好
#include<bits/stdc++.h>
using namespace std;
int dp[102][102];
int getPaths(int m,int n)
{for(int i=0;i<m;i++)dp[i][0] = 1;for(int j=0;j<n;j++)dp[0][j] = 1;for(int i=1;i<m;i++)for(int j=1;j<n;j++)dp[i][j] = dp[i-1][j] + dp[i][j-1];return dp[m-1][n-1];
}
int main()
{int m,n;cin >> m >> n;cout << getPaths(m,n);return 0;
}

 本文作者：小兔子编程 作者首页：小兔子编程-CSDN博客

四、运行结果

3 728

五、考点分析

难度级别：一般，这题相对而言在于最小花费，具体主要考查如下：

1. 分析题目，找到解题思路
2. 充分掌握变量和数组的定义和使用
3. 学会动态规划算法的原理和使用
4. 确定动态数组的定义和含义
5. 分析出动态规划算法的状态转移方程以及遍历顺序
6. 学会输入流对象cin的使用，从键盘读入相应的数据
7. 学会for循环的使用，在确定循环次数的时候推荐使用学会
8. 掌握输出流对象cout的使用，与流插入运算符 << 结合使用将对象输出到终端显示
9. 学会分析题目，算法分析，将复杂问题模块化，简单化，从中找到相应的解题思路
10. 充分掌握变量定义和使用、分支语句、循环语句和动态规划算法的应用

PS：方式方法有多种，小朋友们只要能够达到题目要求即可！

六、推荐资料

• 所有考级比赛学习相关资料合集【推荐收藏】

这篇关于算法学习012-不同路径 c++动态规划算法实现 中小学算法思维学习 信奥算法解析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---