本文主要是介绍leetcode算法笔记-第一章练习题目,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

方法一:暴力枚举
class Solution:def twoSum(self, nums, target):for i in range(len(nums)):for j in range(i+1, len(nums)):if nums[i]+nums[j] == target:return [i,j]return []我们可以看出这是使用了双重循环来遍历求解,算法时间复杂度为,其中n为nums中的元素数量。算法空间复杂度为O(1)。
关于range的一些细节:
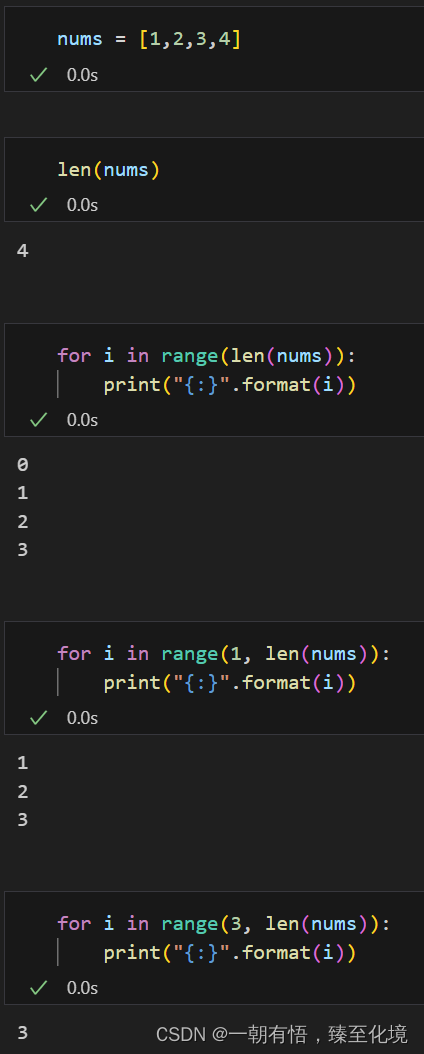
方法二:哈希表:
class Solution:def twoSum(self, nums, target):numDict = dict()for i in range(len(nums)):if target - nums[i] in numDict:return numDict[target - nums[i]], i numDict[nums[i]] = ireturn []我们只用遍历一遍数组,对于当前i,先查找target-nums[i]是否在哈希表中,如果在的话就返回numDict[target-nums[i]]和i;如果不在就把当前的值和其序号存入哈希表中。
请注意:
以上两步不能交换顺序,也就是说不能先把当前值存入后再进行查找。
因为如果这样做的话,同一个数就可能被使用两次,进而导致错误。举例如下:
target:4
nums:[2,1,3]
此时i=0
如果先把2存进去后,此时的numDict中含有(2,0)
然后进行查找
发现4-nums[0]=2在numDict中
这样就会返回0, 0进而导致错误算法时间复杂度为O(n)
算法空间复杂度为O(n)

暴力解法:
class Solution(object):def runningSum(self, nums):result = [0 for i in range(len(nums))]for i in range(len(nums)):for j in range(0, i+1):result[i] = result[i] + nums[j]return result算法时间复杂度
算法空间复杂度O(n)
原地修改法:
直接在原数组上修改
class Solution(object):def runningSum(self, nums):for i in range(1, len(nums)):nums[i] += nums[i-1]return nums
算法时间复杂度为O(n)
算法空间复杂度为O(1)

这题比较有意思
第一种解法,直接使用大小写转换的api
class Solution:def toLowerCase(self, s: str) -> str:return s.lower()
第二种是我自己使用迭代器的转换,主要是是使用了大小写字母之间ASCII码差32的规律
class Solution(object):def toLowerCase(self, s):result = ''.join(ch for ch in [chr(ord(ch1)+32) if 65 <= ord(ch1) <= 90 else ch1 for ch1 in s])return result还有一种类似的,只不过使用了位运算
class Solution:def toLowerCase(self, s: str) -> str:return "".join(chr(asc | 32) if 65 <= (asc := ord(ch)) <= 90 else ch for ch in s)
:=为海象操作符(赋值表达式),它允许在表达式中同时进行赋值和返回值。
这里使用了asc|32:
'A'的ASCII码二进制是0100 0001,因为二进制第6为0,也就是表示32的那一位是0,并且字母只有26位,所以到最后一个字母‘Z'表示32的那一位还是0(32对应二进制0010 0000),所以这样或运算才等于加。但是如果你排在一起,或26是肯定不等于加26的,或运算等于加法情况只能是在对应位为0或相反时成立,不能有相同位置的值为1。所以或32就等同于把第6位从0变到1,方便了字母大小写的转换,同理如果要实现从小写字母变成大写字母的话就需要与上1101 1111也就是223

class Solution(object):def maximumWealth(self, accounts):return max([sum(accounts[i]) for i in range(len(accounts))])class Solution:def maximumWealth(self, accounts: List[List[int]]) -> int:return max(map(sum, accounts))
算法时间复杂度为O(mn),m为网格的行数,n为网格列数。
算法空间复杂度为O(1)
map(function, iterable, ...)
map函数的用法:map允许你将一个函数应用于一个迭代器的每个列并且把产生的结果组成一个迭代器返回。
numbers1 = [1, 2, 3]
numbers2 = [4, 5, 6]result = map(lambda x, y: x + y, numbers1, numbers2)print(list(result))
# 输出: [5, 7, 9]
这篇关于leetcode算法笔记-第一章练习题目的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






