笔试时常用排序算法时间复杂度和空间复杂度

本文主要是介绍笔试时常用排序算法时间复杂度和空间复杂度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘自维基百科： http://zh.wikipedia.org/wiki/%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95#.E7.A8.B3.E5.AE.9A.E6.80.A7

在计算机科学所使用的排序算法通常被分类为：

计算的时间复杂度（最差、平均、和最好性能），依据列表（list）的大小(n)。一般而言，好的性能是O(n log n)，且坏的性能是O(n²)。对于一个排序理想的性能是O(n)。仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要O(n logn)。
存储器使用量（以及其他电脑资源的使用）
稳定性：稳定排序算法会让原本有相等键值的纪录维持相对次序。也就是如果一个排序算法是稳定的，当有两个相等键值的纪录R和S，且在原本的列表中R出现在S之前，在排序过的列表中R也将会是在S之前。
依据排序的方法：插入、交换、选择、合并等等。

稳定性[编辑]

当相等的元素是无法分辨的，比如像是整数，稳定性并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来排序。

(4, 1)  (3, 1)  (3, 7)（5, 6）

在这个状况下，有可能产生两种不同的结果，一个是让相等键值的纪录维持相对的次序，而另外一个则没有：

(3, 1)  (3, 7)  (4, 1)  (5, 6)  （維持次序）
(3, 7)  (3, 1)  (4, 1)  (5, 6)  （次序被改變）

不稳定排序算法可能会在相等的键值中改变纪录的相对次序，但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。作这件事情的一个方式是人工扩充键值的比较，如此在其他方面相同键值的两个对象间之比较，（比如上面的比较中加入第二个标准：第二个键值的大小）就会被决定使用在原先数据次序中的条目，当作一个同分决赛。然而，要记住这种次序通常牵涉到额外的空间负担。

排序算法列表[编辑]

在这个表格中，n是要被排序的纪录数量以及k是不同键值的数量。

稳定的排序[编辑]

冒泡排序（bubble sort）— O(n²)
鸡尾酒排序（cocktail sort）—O(n²)
插入排序（insertion sort）—O(n²)
桶排序（bucket sort）—O(n);需要O(k)额外空间
计数排序（counting sort）—O(n+k);需要O(n+k)额外空间
归并排序（merge sort）—O(n log n);需要O(n)额外空间
原地归并排序— O(n²)
二叉排序树排序（binary tree sort）— O(n log n)期望时间; O(n²)最坏时间;需要O(n)额外空间
鸽巢排序（pigeonhole sort）—O(n+k);需要O(k)额外空间
基数排序（radix sort）—O(n·k);需要O(n)额外空间
侏儒排序（gnome sort）— O(n²)
图书馆排序（library sort）— 时间复杂度通常是O(n log n),需要(1+ε)n额外空间

不稳定的排序[编辑]

选择排序（selection sort）—O(n²)
希尔排序（shell sort）—O(n log² n)如果使用最佳的现在版本
Clover排序算法（Clover sort）—O(n)期望时间，O（n^2/2）最坏情况
梳排序— O(n log n)
堆排序（heap sort）—O(n log n)
平滑排序（smooth sort）— O(n log n)
快速排序（quick sort）—O(n log n)期望时间, O(n²)最坏情况;对于大的、乱数列表一般相信是最快的已知排序
内省排序（introsort）—O(n log n)
耐心排序（patience sort）—O(n log n + k)最坏情况时间，需要额外的O(n + k)空间，也需要找到最长的递增子序列（longest increasing subsequence）

不实用的排序[编辑]

Bogo排序— O(n × n!)，最坏的情况下期望时间为无穷。
Stupid排序—O(n³);递归版本需要O(n²)额外存储器
珠排序（bead sort）— O(n) or O(√n),但需要特别的硬件
煎饼排序—O(n),但需要特别的硬件
臭皮匠排序（stooge sort）算法简单，但需要约n^2.7的时间

平均时间复杂度[编辑]

平均时间复杂度由高到低为：

冒泡排序O(n²)
选择排序O(n²)
插入排序O(n²)
希尔排序O(n^1.25)
堆排序O(n log n)
归并排序O(n log n)
快速排序O(n log n)
基数排序O(n)

说明：虽然完全逆序的情况下，快速排序会降到选择排序的速度，不过从概率角度来说（参考信息学理论，和概率学），不对算法做编程上优化时，快速排序的平均速度比堆排序要快一些。

名称	数据对象	稳定性	时间复杂度		空间复杂度	描述
名称	数据对象	稳定性	平均	最坏	空间复杂度	描述
冒泡排序	数组		$O(n^2)$		$O(1)$	（无序区，有序区）。从无序区通过交换找出最大元素放到有序区前端。
选择排序	数组		$O(n^2)$		$O(1)$	（有序区，无序区）。在无序区里找一个最小的元素跟在有序区的后面。对数组：比较得多，换得少。
选择排序	链表		$O(n^2)$		$O(1)$	（有序区，无序区）。在无序区里找一个最小的元素跟在有序区的后面。对数组：比较得多，换得少。
插入排序	数组、链表		$O(n^2)$		$O(1)$	（有序区，无序区）。把无序区的第一个元素插入到有序区的合适的位置。对数组：比较得少，换得多。
堆排序	数组		$O(n\log n)$		$O(1)$	（最大堆，有序区）。从堆顶把根卸出来放在有序区之前，再恢复堆。
归并排序	数组		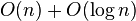$O(n\log n)$		$O(n) +O(\log n)$ ，如果不是从下到上	把数据分为两段，从两段中逐个选最小的元素移入新数据段的末尾。可从上到下或从下到上进行。
归并排序	链表		$O(n\log n)$		$O(1)$	把数据分为两段，从两段中逐个选最小的元素移入新数据段的末尾。可从上到下或从下到上进行。
快速排序	数组		$O(n\log n)$	$O(n^2)$	$O(\log n) ,O(n)$	（小数，枢纽元，大数）。
希尔排序	数组		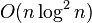$O(n\log^2n)$	$O(n^2)$	$O(1)$	每一轮按照事先决定的间隔进行插入排序，间隔会依次缩小，最后一次一定要是1。

计数排序	数组、链表		$O(n+m)$		$O(n+m)$	统计小于等于该元素值的元素的个数i，于是该元素就放在目标数组的索引i位（i≥0）。
桶排序	数组、链表		$O(n)$		$O(m)$	将值为i的元素放入i号桶，最后依次把桶里的元素倒出来。
基数排序	数组、链表		$O(k\times n)$	$O(n^2)$		一种多关键字的排序算法，可用桶排序实现。