[Algorithm][递归][斐波那契数列模型][第N个泰波那契数][三步问题][使用最小花费爬楼][解码方法]详细讲解

本文主要是介绍[Algorithm][递归][斐波那契数列模型][第N个泰波那契数][三步问题][使用最小花费爬楼][解码方法]详细讲解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.第 N 个泰波那契数
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
2.三步问题
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
3.使用最小花费爬楼梯
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
4.解码方法
- 1.题目链接
- 2.算法原理详解
- 3.代码实现

1.第 N 个泰波那契数

1.题目链接

第 N 个泰波那契数

2.算法原理详解

题目解析：
思路：
- 确定状态表示 -> dp[i]的含义
  - 第i个泰波那契数的值
- 推导状态转移方程
  - dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
- 初始化
  - dp[0] = 0, dp[1] = 1, dp[2] = 1
- 确定填表顺序：从左向右
- 确定返回值：dp[n]
空间优化：滚动数组

3.代码实现

// v1.0 动态规划
int tribonacci(int n) 
{// 边界情况处理if(n == 0 || n == 1) return n;vector<int> dp(n + 1, 0);dp[1] = dp[2] = 1;for(int i = 3; i <= n; i++){dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];}return dp[n];
}
-------------------------------------------------------------------
// v2.0 动态规划 + 滚动数组空间优化
int tribonacci(int n) 
{// 边界情况处理if(n == 0 || n == 1) return n;int a = 0, b = 1, c = 1, ret = 1;for(int i = 3; i <= n; i++){ret = a + b + c;a = b, b = c, c = ret; // 滚动数组}return ret;
}

2.三步问题

1.题目链接

三步问题

2.算法原理详解

题目解析：
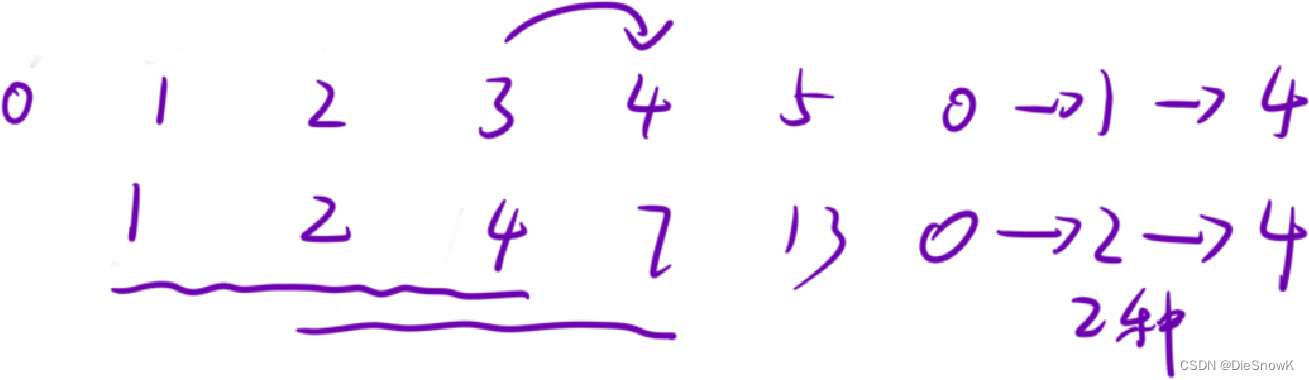
思路：
- 确定状态表示 -> dp[i]的含义
  - 到达i位置时，一共有多少种方法
- 推导状态转移方程
  - dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
- 初始化
  - dp[1] = 1, dp[2] = 2, dp[3] = 4
- 确定填表顺序：从左向右
- 确定返回值：dp[n]

3.代码实现

int waysToStep(int n) 
{// 边界情况处理if(n == 1 || n == 2) return n;if(n == 3) return 4;const int MOD = 1e9 + 7;vector<int> dp(n + 1, 0);dp[1] = 1, dp[2] = 2, dp[3] = 4;for(int i = 4; i <= n; i++){dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;}return dp[n];
}

3.使用最小花费爬楼梯

1.题目链接

使用最小花费爬楼梯

2.算法原理详解

本题给出两种思路，本质相同，只是思考的方向不同
思路一：
- 确定状态表示 -> dp[i]的含义
  - 以i位置为结尾
  - 到达i位置时，最小花费
- 推导状态转移方程
  - dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
- 初始化
  - dp[0] = dp[1] = 0
- 确定填表顺序：从左向右
- 确定返回值：dp[n]
思路二：
- 确定状态表示 -> dp[i]的含义
  - 以i位置为起点
  - 从i位置出发，到达楼顶，此时的最小花费
- 推导状态转移方程
  - dp[i] = cost[i] + min(dp[i + 1], dp[i + 2])
- 初始化
  - dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2]
- 确定填表顺序：从右向左
- 确定返回值：min(dp[0], dp[1])

3.代码实现

// v1.0 以i位置为结尾
int minCostClimbingStairs(vector<int>& cost) 
{int n = cost.size();vector<int> dp(n + 1);for(int i = 2; i <= n; i++){dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[n];
}
----------------------------------------------------------------------------
// v2.0 以i位置为起点
int minCostClimbingStairs(vector<int>& cost) 
{int n = cost.size();vector<int> dp(n);dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2];for(int i = n - 3; i >= 0; i--){dp[i] = cost[i] + min(dp[i + 1], dp[i + 2]);}return min(dp[0], dp[1]);
}

4.解码方法

1.题目链接

解码方法

2.算法原理详解

思路：
- 确定状态表示 -> dp[i]的含义
  - 以i位置为结尾时，解码方法的总数
- 推导状态转移方程
  - 如果条件都成立：dp[i] = dp[i - 1] + dp[i - 2]
- 初始化
  - dp[0]：只解码一个字符
    - 1 <-- 1<=a<=9
    - 0 <-- 0
  - dp[1]：只解码两个字符
    - 0 <-- 解码不出来
    - 1 <-- 两个解码出一个
    - 2 <-- 两个解码出一个 + 一个解码出一个
- 确定填表顺序：从左向右
- 确定返回值：dp[n - 1]
优化边界及初始化：dp表多开一个"虚拟结点"
- 相当于把原来dp[1]放到了后面填表的逻辑当中了，不用进行繁琐的初始化了
- 注意事项：
  - 虚拟节点里面的值，要保证后面填表时是正确的
  - 下标的映射关系
- 怎样处理？
  - 此时dp[1]的初始化相当于原来的dp[0]的初始化，不用做特殊处理
  - dp[0] = 1做特殊处理
    - 因为此时的dp[2]在统一的逻辑里面，会去看dp[0]和dp[1]的值
      - 如果条件都成立：dp[2] = dp[0] + dp[1]
    - 此时如果dp[0] == 0，相当于dp[2]前面少了一种可能

3.代码实现

// v1.0
int numDecodings(string s) 
{int n = s.size();vector<int> dp(n, 0);dp[0] = s[0] != '0';// 处理边界情况if(s.size() == 1) return dp[0];// 一个位置解码出来一个if(s[0] != '0' && s[1] != '0'){dp[1]++;}// 两个位置解码出来一个int tmp = (s[0] - '0') * 10 + s[1] - '0';if(tmp >= 10 && tmp <= 26){dp[1]++;}// Dynamic Planfor(int i = 2; i < n; i++){// 一个位置解码出来一个if(s[i] != '0'){dp[i] += dp[i - 1];}// 两个位置解码出来一个int tmp = (s[i - 1] - '0') * 10 + s[i] - '0';if(tmp >= 10 && tmp <= 26){dp[i] += dp[i - 2];}}return dp[n - 1];
}
----------------------------------------------------------------------
// v2.0 优化
int numDecodings(string s) 
{int n = s.size();vector<int> dp(n + 1, 0);dp[0] = 1;dp[1] = s[0] != '0';// Dynamic Planfor(int i = 2; i <= n; i++){// 一个位置解码出来一个if(s[i - 1] != '0'){dp[i] += dp[i - 1];}// 两个位置解码出来一个int tmp = (s[i - 2] - '0') * 10 + s[i - 1] - '0';if(tmp >= 10 && tmp <= 26){dp[i] += dp[i - 2];}}return dp[n];
}