强化学习实例分析:CartPole【Monte Carlo】

2024-04-25 11:04
文章标签 分析 学习 实例 强化 monte carlo cartpole

本文主要是介绍强化学习实例分析:CartPole【Monte Carlo】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

强化学习笔记

主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程，个人觉得赵老师的课件深入浅出，很适合入门.

第一章 强化学习基本概念
第二章 贝尔曼方程
第三章 贝尔曼最优方程
第四章 值迭代和策略迭代
第五章 强化学习实例分析:GridWorld
第六章 蒙特卡洛方法
第七章 Robbins-Monro算法
第八章 多臂老虎机
第九章 强化学习实例分析:CartPole

文章目录

  • 强化学习笔记
  • 一、问题描述
    • 1 创建环境
    • 2 Take actions
    • 3 States Discretization
  • 二、 On-policy first-visit MC control
  • 三、完整代码
  • 参考资料

在第六章 蒙特卡洛方法中我们学习了蒙特卡洛方法，这一节我们结合强化学习工具包gym中的CartPole问题来复现蒙特卡洛方法中的On-policy first-visit MC control算法。CartPole问题是一个经典的强化学习示例，旨在通过控制一个倒立摆的平衡杆，使其保持直立状态。Monte Carlo方法则是解决这类问题的一种策略。

在本文中，我们将深入探讨CartPole问题，并重点分析Monte Carlo方法在解决这一问题中的应用。我们将从基本概念出发，介绍CartPole问题的背景和目标，然后详细解释Monte Carlo方法的原理和实现方式。通过实例分析，我们将揭示Monte Carlo方法如何在CartPole问题中发挥作用，以及它是如何帮助智能体学习和改进其策略的。

一、问题描述

1 创建环境

CartPole问题描述如下：

  1. 一根杆子由一个非驱动的关节连接到一辆小车上，小车沿着一条无摩擦的轨道移动。
  2. 该系统通过对推车施加+1或-1的力来控制。
  3. Pole开始直立，我们的目的是让它保持直立。
  4. 柱子保持直立的每一个时间步都将提供+1的奖励。
  5. 当杆子偏离垂直方向超过15度，或推车偏离中心方向超过2.4个单位时，这一episode结束。
  6. 更多信息(参见GITHUB上的源代码)。

下面的例子展示了这个测试环境的基本用法:

import gym
import numpy as np
import matplotlib.pyplot as plt
env = gym.make('CartPole-v1')
observation = env.reset() ##Initial an episodeprint("Inital observation is {}".format(observation))print("\nThis means the cart current position is {}".format(observation[0][0]), end = '')
print(" with velocity {},".format(observation[0][1]))print("and the pole current angular position is {}".format(observation[0][2]), end = '')
print(" with angular velocity {},".format(observation[0][3]))

输出为：

截屏2024-04-24 18.47.34

2 Take actions

使用env.step(action)执行操作，action取0或1：0:“向左”;1:“向右”.

print("Current observation is {}".format(observation))action = 0 #go left
observation, reward, done, info,_ = env.step(action)print("\nNew observation is {}".format(observation))
print("Step reward is {}".format(reward))
print("Did episode just ends? -{}".format(done))

输出如下，我们可以看到位置确实向左移动了。

截屏2024-04-24 18.49.53

3 States Discretization

类DiscreteObs()将观测空间离散化为离散状态空间，表格法需要对观测空间进行离散化。

class DiscretObs():def __init__(self, bins_list):self._bins_list = bins_listself._bins_num = len(bins_list)self._state_num_list = [len(bins)+1 for bins in bins_list]self._state_num_total = np.prod(self._state_num_list)def get_state_num_total(self):return self._state_num_totaldef obs2state(self, obs):if not len(obs)==self._bins_num:raise ValueError("observation must have length {}".format(self._bins_num))else:return [np.digitize(obs[i], bins=self._bins_list[i]) for i in range(self._bins_num)]def obs2idx(self, obs):state = self.obs2state(obs)return self.state2idx(state)def state2idx(self, state):idx = 0for i in range(self._bins_num-1,-1,-1):idx = idx*self._state_num_list[i]+state[i]return idxdef idx2state(self, idx):state = [None]*self._bins_numstate_num_cumul = np.cumprod(self._state_num_list)for i in range(self._bins_num-1,0,-1):state[i] = idx/state_num_cumul[i-1]idx -=state[i]*state_num_cumul[i-1]state[0] = idx%state_num_cumul[0]return state# Recommended Discretization for Carpole-v1 when using Monte-Carlo methods
bins_pos = np.linspace(-2.4,2.4,40)        # position
bins_d_pos = np.linspace(-3,3,5)           # velocity
bins_ang = np.linspace(-0.2618,0.2618,40)  # angle
bins_d_ang = np.linspace(-0.3,0.3,5)       # angular velocitydobs = DiscretObs([bins_pos,bins_d_pos,bins_ang,bins_d_ang])
observation = env.reset()[0]state = dobs.obs2state(observation)
idx = dobs.obs2idx(observation)print("Current position of the cart is {:.4f}\n".format(observation[0]))
print("Current velocity of the cart is {:.4f}\n".format(observation[1]))
print("Current angular position of the pole is {:.4f} rad\n".format(observation[2]))
print("Current angular velocity of the pole is {:.4f} rad\n".format(observation[3]))print("which are mapped to state {}, with corresponding index {}".format(state,idx))

输出如下，我们将连续的状态值离散化，映射到整数空间：

截屏2024-04-24 18.53.08

二、 On-policy first-visit MC control

下面我们就可以来实现在蒙特卡洛方法 介绍的On-policy first-visit MC control算法。get_action函数实现 ε \varepsilon ε-greedy策略，基于当前的状态和估计的 Q Q Q返回应该采取的动作。

def get_action(current_state, Q, epsilon):if np.random.random() < epsilon:return env.action_space.sample()  # Random actionelse:return np.argmax(Q[current_state])  # Greedy action

update_Q函数根据每个episode的数据来更新 Q Q Q的估计值，采用的是first-visit，只用第一次出现的(s,a)来更新 Q ( s , a ) Q(s,a) Q(s,a)：

def update_Q(Q, returns, Returns, observation_list, action_list, gamma=0.99): G = 0ob_act_list = [(dobs.obs2idx(observation_list[i]), action_list[i]) for i in range(len(observation_list))]for i in range(len(returns)-1,-1,-1):obs = observation_list[i]act = action_list[i]state_idx = dobs.obs2idx(obs)index = ob_act_list.index((state_idx,act)) # find the first occurence of (s,a) in the episodeif i == index:     # if (s,a) is not visited in the episode before,i.e. first-visitG = gamma * G + returns[i]if (state_idx, act) not in Returns:Returns[(state_idx, act)] = (G, 1)else:Returns[(state_idx, act)] = (Returns[(state_idx, act)][0] + G, Returns[(state_idx, act)][1] + 1)else:continueQ[state_idx][act] = Returns[(state_idx, act)][0] / Returns[(state_idx, act)][1] # q(s,a) = average of Returns(s,a)return Q

下面我们来进行实验：

# Initialize environment and parameters
env = gym.make('CartPole-v1',render_mode='rgb_array')
epsilon_start = 0.3
epsilon_decay_rate = 0.97
num_episodes = 40000
set_size = 2000
set_num = num_episodes // set_size
Q = np.random.uniform(low=-1, high=1, size=(dobs.get_state_num_total(), env.action_space.n))rewards = []
epsilon = epsilon_start
Returns = {}for ep in range(num_episodes):observation = env.reset()[0]done = Falseobservation_list = []action_list = []returns = []while not done:current_state = dobs.obs2idx(observation)action = get_action(current_state, Q, epsilon)observation_list.append(observation)action_list.append(action)observation, reward, done, info,_ = env.step(action)returns.append(reward)Q = update_Q(Q, returns, Returns, observation_list, action_list)rewards.append(sum(returns))if (ep + 1) % set_size == 0:epsilon *= epsilon_decay_rate  # Decay epsilon# Every 2000 episodes, compute the average rewardif (ep + 1) % set_size == 0:print(f"Average reward for episodes {ep-set_size+2}-{ep+1}: {np.mean(rewards[-set_size:])}")# Compute and plot average rewards per set
average_rewards_per_set = [np.mean(rewards[i:i+set_size]) for i in range(0, num_episodes, set_size)]
plt.figure(figsize=(12, 6),dpi=150)
plt.plot(range(1, set_num + 1), average_rewards_per_set, marker='o', linestyle='-')
plt.xlabel('Set Number (2000 episodes/set)')
plt.ylabel('Set average reward')
plt.title('Average Reward per Set Over 40,000 Episodes')
plt.grid(True)
plt.show()

经过半个小时的训练，总算结束，如下图所示，我们可以看到随着实验次数增加，我们每2000个episode得到的奖励越来越多，说明我们对 Q Q Q的估计越来越准确。但我们也能看到蒙特卡洛法的缺点，效率低！对连续空间进行离散化，会导致维度灾难和样本效率低下，在这个例子中充分的体现了这一点。

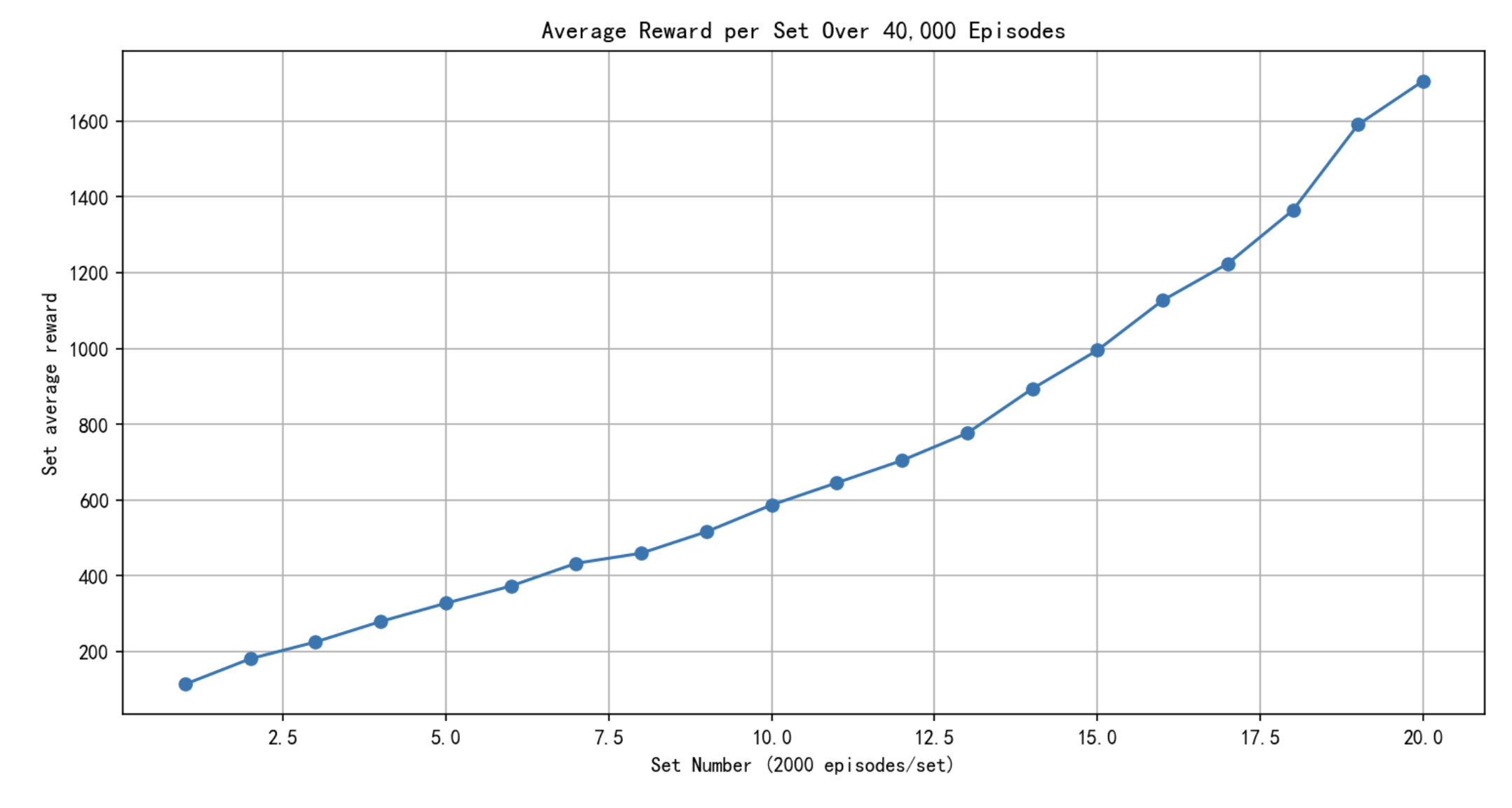
截屏2024-04-24 19.36.26

下面我们利用现在学习到的 Q Q Q值采用贪心算法来控制模型，发现在很长时间还是能够保证pole直立的。

# Use greedy policy of the trained Q function to control the carpole for 100 episode, 
env = gym.make('CartPole-v1',render_mode='rgb_array')
observation = env.reset()[0]# create a figure and axis to display the environment
plt.figure()
img = plt.imshow(env.render()) 
while 1:img.set_data(env.render())  # update the imagedisplay.display(plt.gcf())display.clear_output(wait=True)current_state = dobs.obs2idx(observation)      # discretize the observation spaceaction = np.argmax(Q[current_state])           # choose action by greedy policy of the trained Qobservation, reward, done, info, _ = env.step(action)if done:break

cartpole

三、完整代码

import gym
import matplotlib.pyplot as plt
from IPython import display
import numpy as npclass DiscretObs():def __init__(self, bins_list):self._bins_list = bins_listself._bins_num = len(bins_list)self._state_num_list = [len(bins)+1 for bins in bins_list]self._state_num_total = np.prod(self._state_num_list)def get_state_num_total(self):return self._state_num_totaldef obs2state(self, obs):if not len(obs)==self._bins_num:raise ValueError("observation must have length {}".format(self._bins_num))else:return [np.digitize(obs[i], bins=self._bins_list[i]) for i in range(self._bins_num)]def obs2idx(self, obs):state = self.obs2state(obs)return self.state2idx(state)def state2idx(self, state):idx = 0for i in range(self._bins_num-1,-1,-1):idx = idx*self._state_num_list[i]+state[i]return idxdef idx2state(self, idx):state = [None]*self._bins_numstate_num_cumul = np.cumprod(self._state_num_list)for i in range(self._bins_num-1,0,-1):state[i] = idx/state_num_cumul[i-1]idx -=state[i]*state_num_cumul[i-1]state[0] = idx%state_num_cumul[0]return state# Recommended Discretization for Carpole-v1 when using Monte-Carlo methods
bins_pos = np.linspace(-2.4,2.4,40)        # position
bins_d_pos = np.linspace(-3,3,5)           # velocity
bins_ang = np.linspace(-0.2618,0.2618,40)  # angle
bins_d_ang = np.linspace(-0.3,0.3,5)       # angular velocitydobs = DiscretObs([bins_pos,bins_d_pos,bins_ang,bins_d_ang])def get_action(current_state, Q, epsilon):if np.random.random() < epsilon:return env.action_space.sample()  # Random actionelse:return np.argmax(Q[current_state])  # Greedy actiondef update_Q(Q, returns, Returns, observation_list, action_list, gamma=0.99): G = 0ob_act_list = [(dobs.obs2idx(observation_list[i]), action_list[i]) for i in range(len(observation_list))]for i in range(len(returns)-1,-1,-1):obs = observation_list[i]act = action_list[i]state_idx = dobs.obs2idx(obs)index = ob_act_list.index((state_idx,act)) # find the first occurence of (s,a) in the episodeif i == index:     # if (s,a) is not visited in the episode before,i.e. first-visitG = gamma * G + returns[i]if (state_idx, act) not in Returns:Returns[(state_idx, act)] = (G, 1)else:Returns[(state_idx, act)] = (Returns[(state_idx, act)][0] + G, Returns[(state_idx, act)][1] + 1)else:continueQ[state_idx][act] = Returns[(state_idx, act)][0] / Returns[(state_idx, act)][1] # q(s,a) = average of Returns(s,a)return Q# Initialize environment and parameters
env = gym.make('CartPole-v1',render_mode='rgb_array')
epsilon_start = 0.3
epsilon_decay_rate = 0.97
num_episodes = 40000
set_size = 2000
set_num = num_episodes // set_size
Q = np.random.uniform(low=-1, high=1, size=(dobs.get_state_num_total(), env.action_space.n))rewards = []
epsilon = epsilon_start
Returns = {}for ep in range(num_episodes):observation = env.reset()[0]done = Falseobservation_list = []action_list = []returns = []while not done:current_state = dobs.obs2idx(observation)action = get_action(current_state, Q, epsilon)observation_list.append(observation)action_list.append(action)observation, reward, done, info,_ = env.step(action)returns.append(reward)Q = update_Q(Q, returns, Returns, observation_list, action_list)rewards.append(sum(returns))if (ep + 1) % set_size == 0:epsilon *= epsilon_decay_rate  # Decay epsilon# Every 2000 episodes, compute the average rewardif (ep + 1) % set_size == 0:print(f"Average reward for episodes {ep-set_size+2}-{ep+1}: {np.mean(rewards[-set_size:])}")# Compute and plot average rewards per set
average_rewards_per_set = [np.mean(rewards[i:i+set_size]) for i in range(0, num_episodes, set_size)]
plt.figure(figsize=(12, 6),dpi=150)
plt.plot(range(1, set_num + 1), average_rewards_per_set, marker='o', linestyle='-')
plt.xlabel('Set Number (2000 episodes/set)')
plt.ylabel('Set average reward')
plt.title('Average Reward per Set Over 40,000 Episodes')
plt.grid(True)
plt.show()

参考资料

  1. Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.

这篇关于强化学习实例分析:CartPole【Monte Carlo】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/934496。

相关文章

Java程序进程起来了但是不打印日志的原因分析

Java程序进程起来了但是不打印日志的原因分析

《Java程序进程起来了但是不打印日志的原因分析》：本文主要介绍Java程序进程起来了但是不打印日志的原因分析,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录Java程序进程起来了但是不打印日志的原因1、日志配置问题2、日志文件权限问题3、日志文件路径问题4、程序
阅读更多...
Java字符串操作技巧之语法、示例与应用场景分析

Java字符串操作技巧之语法、示例与应用场景分析

《Java字符串操作技巧之语法、示例与应用场景分析》在Java算法题和日常开发中,字符串处理是必备的核心技能,本文全面梳理Java中字符串的常用操作语法,结合代码示例、应用场景和避坑指南,可快速掌握字... 目录引言1. 基础操作1.1 创建字符串1.2 获取长度1.3 访问字符2. 字符串处理2.1 子字
阅读更多...
Vue3组件中getCurrentInstance()获取App实例,但是返回null的解决方案

Vue3组件中getCurrentInstance()获取App实例,但是返回null的解决方案

《Vue3组件中getCurrentInstance()获取App实例,但是返回null的解决方案》：本文主要介绍Vue3组件中getCurrentInstance()获取App实例,但是返回nu... 目录vue3组件中getCurrentInstajavascriptnce()获取App实例，但是返回n
阅读更多...
SQL表间关联查询实例详解

SQL表间关联查询实例详解

《SQL表间关联查询实例详解》本文主要讲解SQL语句中常用的表间关联查询方式,包括：左连接（leftjoin）、右连接（rightjoin）、全连接（fulljoin）、内连接（innerjoin）、... 目录简介样例准备左外连接右外连接全外连接内连接交叉连接自然连接简介本文主要讲解SQL语句中常用的表
阅读更多...
Python 迭代器和生成器概念及场景分析

Python 迭代器和生成器概念及场景分析

《Python迭代器和生成器概念及场景分析》yield是Python中实现惰性计算和协程的核心工具,结合send()、throw()、close()等方法,能够构建高效、灵活的数据流和控制流模型,这... 目录迭代器的介绍自定义迭代器省略的迭代器生产器的介绍yield的普通用法yield的高级用法yidle
阅读更多...
C++ Sort函数使用场景分析

C++ Sort函数使用场景分析

《C++Sort函数使用场景分析》sort函数是algorithm库下的一个函数,sort函数是不稳定的,即大小相同的元素在排序后相对顺序可能发生改变,如果某些场景需要保持相同元素间的相对顺序,可使... 目录C++ Sort函数详解一、sort函数调用的两种方式二、sort函数使用场景三、sort函数排序
阅读更多...
kotlin中const 和val的区别及使用场景分析

kotlin中const 和val的区别及使用场景分析

《kotlin中const和val的区别及使用场景分析》在Kotlin中,const和val都是用来声明常量的,但它们的使用场景和功能有所不同,下面给大家介绍kotlin中const和val的区别,... 目录kotlin中const 和val的区别1. val:2. const:二 代码示例1 Java
阅读更多...
Go标准库常见错误分析和解决办法

Go标准库常见错误分析和解决办法

《Go标准库常见错误分析和解决办法》Go语言的标准库为开发者提供了丰富且高效的工具,涵盖了从网络编程到文件操作等各个方面,然而,标准库虽好,使用不当却可能适得其反,正所谓工欲善其事,必先利其器,本文将... 目录1. 使用了错误的time.Duration2. time.After导致的内存泄漏3. jsO
阅读更多...
C# WinForms存储过程操作数据库的实例讲解

C# WinForms存储过程操作数据库的实例讲解

《C#WinForms存储过程操作数据库的实例讲解》：本文主要介绍C#WinForms存储过程操作数据库的实例,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录一、存储过程基础二、C# 调用流程1. 数据库连接配置2. 执行存储过程（增删改）3. 查询数据三、事务处
阅读更多...
springboot security验证码的登录实例

springboot security验证码的登录实例

《springbootsecurity验证码的登录实例》：本文主要介绍springbootsecurity验证码的登录实例,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,... 目录前言代码示例引入依赖定义验证码生成器定义获取验证码及认证接口测试获取验证码登录总结前言在spring
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2