自动驾驶---OpenSpace之Hybrid A*规划算法

本文主要是介绍自动驾驶---OpenSpace之Hybrid A*规划算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 背景

        笔者在上周发布的博客《自动驾驶---低速场景之记忆泊车》中，大体介绍了记忆泊车中的整体方案，其中详细阐述了planning模块的内容，全局规划及局部规划（会车）等内容，包括使用的算法，但是没有深入详细地展开讲述OpenSpace规划算法，因此在本篇博客中，详细讲解该部分内容。

        OpenSpace规划主要涉及到自动驾驶车辆在开放、非结构化环境中的路径规划问题。这种规划对于没有固定参考线的场景特别重要，比如自主泊车、路边停车，城区路口掉头等。

        在OpenSpace规划中，算法的核心是根据感知信息和感兴趣区域（ROI）来生成和选择最佳的行驶路径。感知信息主要包括周围动静态障碍物的位置、速度等信息，而ROI则包含了地图信息，比如道路边界、车位边界等。

        OpenSpace规划算法的基本流程如下：

1. 生成可行驶区域：根据感知数据和地图信息，算法首先会确定车辆可以安全行驶的区域。这通常涉及到对道路边界、障碍物位置等信息的解析和处理。
2. 路径搜索与选择：在确定了可行驶区域后，算法会在这个区域内搜索可能的行驶路径。这个过程可能会使用到各种路径搜索算法，比如A*算法或其变种。搜索到的路径会基于一定的评价标准（比如安全性、效率等）进行排序和选择。
3. 轨迹优化：选定了路径后，算法还需要对车辆的行驶轨迹进行优化，以确保车辆在行驶过程中的平稳性和舒适性。这通常涉及到对车辆运动学模型和动力学模型的考虑，以及使用优化算法来求解最优的轨迹。

        此外，OpenSpace规划还需要考虑一些额外的因素，比如交通规则、行人和其他车辆的动态行为等。这些因素都可能对车辆的行驶路径产生影响，因此需要在规划过程中进行充分的考虑和处理。

        OpenSpace规划是自动驾驶技术中的一个重要环节，它能够帮助车辆在没有固定参考线的开放环境中实现安全、高效的行驶。随着自动驾驶技术的不断发展，OpenSpace规划也将不断优化和完善，以适应更加复杂和多变的环境。

2 OpenSpace规划算法介绍

        OpenSpace规划在自动驾驶中涵盖了多种算法，这些算法共同协作以在开放、非结构化环境中实现安全、高效的路径规划。以下是一些主要的OpenSpace规划算法：

1. Hybrid A*算法：

   • A*算法：传统的A*算法是一种广泛使用的路径搜索算法，它能够在给定的图或网格中找到从起点到终点的最短路径。
   • Hybrid A*算法：针对自动驾驶场景，混合A*算法结合了A*算法与车辆运动学模型，考虑了车辆的实际运动约束，从而生成更符合车辆行驶特性的路径。

2. OBCA算法：

   • MPC预测模型：模型预测控制（MPC）是一种优化控制方法，用于处理具有约束的线性或非线性系统。在OBCA算法中，MPC预测模型用于预测车辆在未来一段时间内的状态，为路径规划提供基础。
   • MPC约束设计：约束设计是确保车辆在行驶过程中遵守交通规则、避免碰撞等的重要步骤。OBCA算法中的MPC约束设计考虑了车辆的运动学约束、避障约束等。
   • MPC目标函数设计：目标函数是优化问题的核心，它定义了优化的目标和评价标准。在OBCA算法中，MPC目标函数设计旨在实现路径的平滑性、安全性以及效率性。

3. SCP路径平滑算法：SCP（Sequential Convex Programming）是一种基于凸优化的启发式算法，用于解决非凸优化问题。在OpenSpace规划中，SCP路径平滑算法用于对搜索到的路径进行平滑处理，提高路径的连续性和舒适性。

        上述这些算法在OpenSpace规划中各自发挥着重要作用，并相互协作以实现自动驾驶车辆在开放空间中的安全、高效行驶。随着技术的不断发展，新的算法和方法也将不断被引入到OpenSpace规划中，以应对更加复杂和多变的环境。

        下面笔者将介绍目前量产中使用比较多的算法：Hybrid A*。从市面上量产的产品及笔者从行业内了解到的信息来看，目前市面上看到华为、大疆、小米和百度使用到该算法，其它家暂时不清楚。

3 Hybrid A*算法介绍

3.1 A*算法介绍

        在介绍Hybrid A*之前，笔者会先介绍A*算法，Hybrid A*算法其实是由A*演变而来（A*算法又由D*算法演化而来，这里就不往前追溯了）。

        A*算法起源于1968年，由Peter E. Hart、Nilsson和Raphael在他们的论文《A Formal Basis for the Heuristic Determination of Minimum Cost Paths in Graphs》中首次提出，该算法是求解静态路网中最短路径问题的一种有效方法，同时也是解决许多搜索问题的有力工具。

        下面先介绍A*算法：

        假设start为起始节点，那么在网格中下一步可扩展的节点数量为8个。

        关于障碍物，在Grid Map中，如果存在障碍物会将生成的网格状态变成不可用，即在节点选择中为不可选的状态。如下图所示（左边可选节点数量为8，右边可选节点数量为7）。

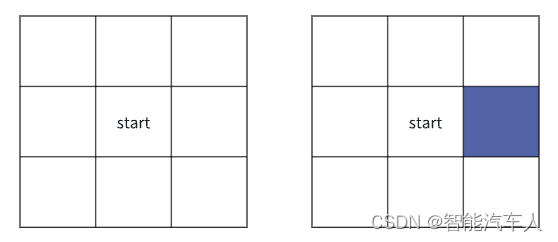
        那么如何选择下一个节点呢？因此引入了一个概念：代价函数。

        代价函数的意思就是这次选择你，付出的代价是多少，定义为f(n)。在A*中代价函数的定义有两个，第一个是已经走过的路径的代价g(n)，另一个是还没有走过的路径的代价h(n)。走过的路径很容易理解，没走过的路径是指从当前节点走到目标节点的距离，在算法中可使用曼哈顿距离或者欧式距离，这里是不考虑障碍物的。

        那么最终周围的每一个可用节点都有一个代价值：f(n) = g(n) + h(n)，如下图所示。

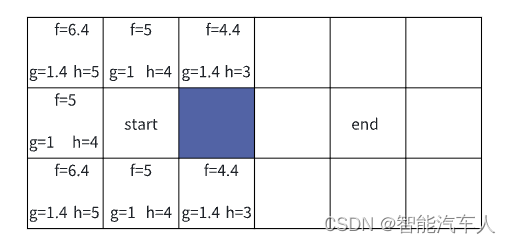
         A*算法的逻辑结构如下：

1. 初始化。从上游获取 grid map信息，设置起点 start、终点 end、栅格数量 m*n 等。
2. 数据预处理。定义 “待计算子节点” 的数组 openlist 以及 “已选中的节点” 的数组 closelist，保存路径的数组 path_closelist。并且还需建立一个当前子节点集合 children，用来保存当前父节点周围8个子节点的坐标，以及父节点本身 parent；还有保存代价值 g , h , f 的数组openlist_cost 和 closelist_cost。
3. 对子节点们 children 中的每个节点 child：若该子节点不在 “待计算子节点” 节点 openlist 中，则追加进去；若在，则计算出该 child 的 g 值，该 g 值是从起点到父节点 parent 的距离加上父节点到该子节点的距离。若该 g 值小于之前 openlist_cost 中的 g 最小值，那么就将openlist_cost 中的最小 g 值更新；
4. 由于该代价最小点已经加入了轨迹，因此将该点加入 clost_list 和 path_closelist，并从openlist 中剔除；
5. 更新 openlist 中的最小代价值，并以其为父节点开始新一轮搜索。

        A*算法最为核心的部分，就在于它的估值函数的设计上：f(n)=g(n)+h(n)。

3.2 Hybrid A*算法

        最早的Hybrid A*算法来自于斯坦福大学无人车团队发表的《Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments》。

        两者的主要区别如下：

算法种类	是否考虑障碍物	是否考虑运动约束	增加的曲线扩展方式
A*	是	否	无
Hybrid A*	是	是	RS曲线

        A*以及Hybrid A*节点的扩展方式见下图所示，在Hybrid A*中考虑了车辆的运动学约束，因此扩展出来的轨迹更符合车辆的实际轨迹。

（1）Reeds Shepp曲线    

        在Hybrid A*中，使用了Reeds Shepp曲线（直线-圆弧的48种组合曲线）去拓展节点，由于Reeds Shepp曲线生成比较简单且快速，所以初始的构造过程是没有考虑碰撞检测的，可以在构造完成后再进行碰撞检测，如果整条轨迹没有碰撞，则放入备选轨迹之中。这里有一个问题可以思考：如果遍历的节点上万个甚至更多，每一个节点都去进行RS扩展的碰撞检测，耗时如何解决？

（2）代价函数的定义

        相比A*算法，其中有一个大的变化在于代价函数的使用，在g(n)的计算中，增加了换挡、转向的代价；在h(n)的计算中，采用了两个子函数，h1(n)表示符合车辆运动学约束但是忽略障碍物的最短路径，h2(n)表示满足障碍物约束但是忽略车辆运动学约束的最短路径，取两者之中的最大值。

（3）Voronoi势场函数

        最后还有一个大的区别：Voronoi势场函数。最终生成的路径保证安全，因此需要距离障碍物有一定的距离。该函数的意义在于：在比较开阔的区域轨迹远离障碍物，在狭窄的区域也可以充分利用空间。

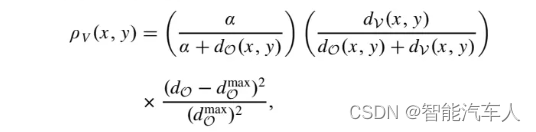
        其中， 表示路径节点到最近障碍物的距离， 表示最近的GVD（Generalized Voronoi Diagram）的长度， 来控制势场的衰减率， 控制势场的最大影响范围。如下图所示，颜色越黑的地方说明势场较大。

 主要代码如下（展示的是Apollo的源代码，相对原始算法做了一些改动）：

bool HybridAStar::Plan(double sx, double sy, double sphi, double ex, double ey, double ephi,const std::vector<double>& XYbounds,const std::vector<std::vector<common::math::Vec2d>>& obstacles_vertices_vec,HybridAStartResult* result) {// clear containersopen_set_.clear();close_set_.clear();open_pq_ = decltype(open_pq_)();final_node_ = nullptr;std::vector<std::vector<common::math::LineSegment2d>>obstacles_linesegments_vec;for (const auto& obstacle_vertices : obstacles_vertices_vec) {size_t vertices_num = obstacle_vertices.size();std::vector<common::math::LineSegment2d> obstacle_linesegments;for (size_t i = 0; i < vertices_num - 1; ++i) {common::math::LineSegment2d line_segment = common::math::LineSegment2d(obstacle_vertices[i], obstacle_vertices[i + 1]);obstacle_linesegments.emplace_back(line_segment);}obstacles_linesegments_vec.emplace_back(obstacle_linesegments);}obstacles_linesegments_vec_ = std::move(obstacles_linesegments_vec);// load XYboundsXYbounds_ = XYbounds;// load nodes and obstaclesstart_node_.reset(new Node3d({sx}, {sy}, {sphi}, XYbounds_, planner_open_space_config_));end_node_.reset(new Node3d({ex}, {ey}, {ephi}, XYbounds_, planner_open_space_config_));if (!ValidityCheck(start_node_)) {ADEBUG << "start_node in collision with obstacles";return false;}if (!ValidityCheck(end_node_)) {ADEBUG << "end_node in collision with obstacles";return false;}double map_time = Clock::NowInSeconds();grid_a_star_heuristic_generator_->GenerateDpMap(ex, ey, XYbounds_,obstacles_linesegments_vec_);ADEBUG << "map time " << Clock::NowInSeconds() - map_time;// load open set, pqopen_set_.emplace(start_node_->GetIndex(), start_node_);open_pq_.emplace(start_node_->GetIndex(), start_node_->GetCost());// Hybrid A* beginssize_t explored_node_num = 0;double astar_start_time = Clock::NowInSeconds();double heuristic_time = 0.0;double rs_time = 0.0;while (!open_pq_.empty()) {// take out the lowest cost neighboring nodeconst std::string current_id = open_pq_.top().first;open_pq_.pop();std::shared_ptr<Node3d> current_node = open_set_[current_id];// check if an analystic curve could be connected from current// configuration to the end configuration without collision. if so, search// ends.const double rs_start_time = Clock::NowInSeconds();if (AnalyticExpansion(current_node)) {break;}const double rs_end_time = Clock::NowInSeconds();rs_time += rs_end_time - rs_start_time;close_set_.emplace(current_node->GetIndex(), current_node);for (size_t i = 0; i < next_node_num_; ++i) {std::shared_ptr<Node3d> next_node = Next_node_generator(current_node, i);// boundary check failure handleif (next_node == nullptr) {continue;}// check if the node is already in the close setif (close_set_.find(next_node->GetIndex()) != close_set_.end()) {continue;}// collision checkif (!ValidityCheck(next_node)) {continue;}if (open_set_.find(next_node->GetIndex()) == open_set_.end()) {explored_node_num++;const double start_time = Clock::NowInSeconds();CalculateNodeCost(current_node, next_node);const double end_time = Clock::NowInSeconds();heuristic_time += end_time - start_time;open_set_.emplace(next_node->GetIndex(), next_node);open_pq_.emplace(next_node->GetIndex(), next_node->GetCost());}}}if (final_node_ == nullptr) {ADEBUG << "Hybrid A searching return null ptr(open_set ran out)";return false;}if (!GetResult(result)) {ADEBUG << "GetResult failed";return false;}ADEBUG << "explored node num is " << explored_node_num;ADEBUG << "heuristic time is " << heuristic_time;ADEBUG << "reed shepp time is " << rs_time;ADEBUG << "hybrid astar total time is "<< Clock::NowInSeconds() - astar_start_time;return true;
}

        由Hybrid A*生成的粗糙轨迹是不能直接给控制使用的，需要进行轨迹平滑，平滑的方法有很多种，这里同样可使用行车的平滑方法《自动驾驶---Motion Planning之参考线Path平滑》（非原文中使用的方法）。最终呈现的效果如下：

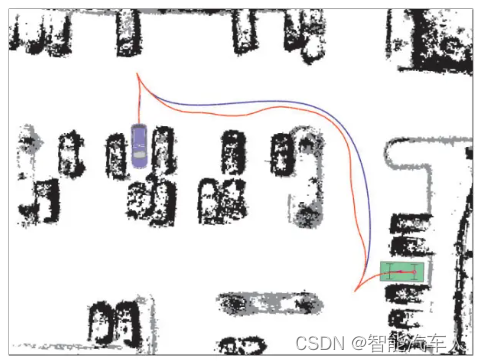
4 展望

        OpenSpace算法不仅适用于泊车场景，也可适用于行车场景。目前各家都在卷城区自动驾驶，那么在城区的狭窄路段需要前后多次调整（比如城市道路常见的U型弯场景，方向盘打到最大无法一次性通过，需要多次腾挪），再比如单车道会车的场景，也需要退让的场景，所以掌握OpenSpace方法对于各家公司规划的 “行泊一体” 也是很有帮助的。

这篇关于自动驾驶---OpenSpace之Hybrid A*规划算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---