本文主要是介绍算法练习第17天|104.二叉树的最大深度 、559.N叉树的最大深度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
104.二叉树的最大深度
104. 二叉树的最大深度 - 力扣（LeetCode）
https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/
什么是二叉树的深度和高度？
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。最大深度==二叉树的层数==根节点的深度==根节点的高度==第二层节点的最大高度+1。
二叉树某个节点的深度：指从根节点到该节点的最长简单路径边的条数。
二叉树某个节点的高度：指从该节点到叶子节点的最长简单路径边的条数。
题目描述：
给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1：
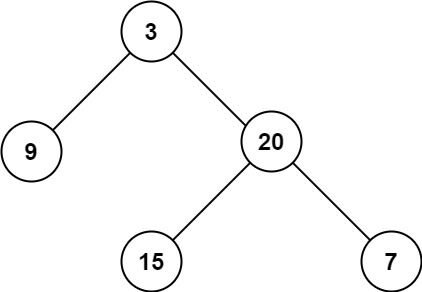
输入：root = [3,9,20,null,null,15,7] 输出：3
示例 2：
输入：root = [1,null,2] 输出：2
思路分析：
本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。
后序递归解法
下面先尝试使用后序递归实现最大深度的求法。
递归第一步：确认递归函数的参数和返回值。题目已经给出，参数为二叉树的根节点指针，返回值为最大深度，所以返回值类型为int。
int maxDepth(TreeNode* root){}递归第二步：确认终止条件。那就是如果传入的root为nullptr，则返回0。即递归结束的条件为空树，即没有子树可以继续下一层的递归。
if(root == nullptr) return 0;递归第三步：确认单层递归逻辑。按照该思路，在单层递归时应该分别统计当前root（可以时根节点，也可以是子树的根节点）的左右子树的最大高度，然后取两者中的最大值。则当前root的深度为两者中的最大值+1，即：
//左子树的高度
int left = maxDepth(root->left);
//右子树的高度
int right = maxDepth(root->right);int depth = max(left, right) + 1; //中
return depth;后序整体代码如下：
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://采用后序递归遍历int maxDepth(TreeNode* root) {if(root == nullptr) return 0;//左子树的高度int left = maxDepth(root->left); //左//右子树的高度int right = maxDepth(root->right); //右int depth = max(left, right) + 1; //中return depth;}
};层序遍历解法
由于二叉树的最大深度就是二叉树的层数，所以使用前文所讲的层序遍历来计算深度（层数）。具体代码如下：
class Solution {
public://采用层序遍历int maxDepth(TreeNode* root) {if(root == nullptr) return 0;queue<TreeNode*> que;que.push(root);int depth = 0;while(!que.empty()){ int size= que.size(); //当前层存在，深度++++depth; //遍历当前层各节点 for(int i=0; i<size; i++){//去每一层的各节点必须放在for循环里TreeNode *node = que.front();que.pop();if(node->left) que.push(node->left);if(node->right) que.push(node->right);}}return depth;}
};前序递归解法
最后介绍一下前序解法，我理解来比较困难，大家可以看一下：
class solution {
public:int result;void getdepth(TreeNode* node, int depth) {result = depth > result ? depth : result; // 中if (node->left == NULL && node->right == NULL) return ;if (node->left) { // 左depth++; // 深度+1getdepth(node->left, depth);depth--; // 回溯，深度-1}if (node->right) { // 右depth++; // 深度+1getdepth(node->right, depth);depth--; // 回溯，深度-1}return ;}int maxDepth(TreeNode* root) {result = 0;if (root == NULL) return result;getdepth(root, 1);return result;}
};559.N叉树的最大深度
559. N 叉树的最大深度 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/description/
题目描述：
给定一个 N 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。
示例 1：
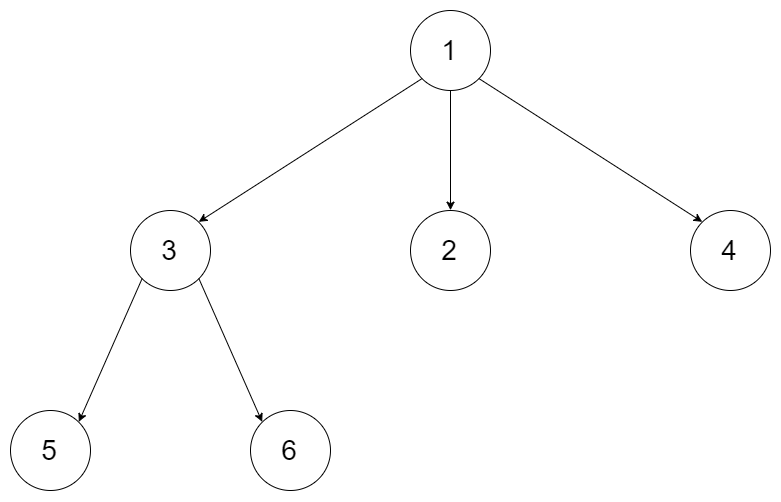
输入：root = [1,null,3,2,4,null,5,6] 输出：3
示例 2：
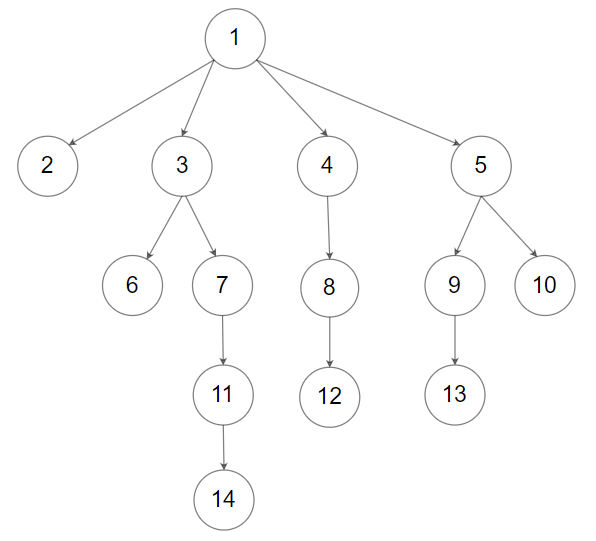
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出：5
有了前面二叉树的解法，下面直接给出后序递归解法：
后序递归解法
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:int maxDepth(Node* root) {if(root == nullptr) return 0;int depth = 0;for(int i = 0; i < root->children.size(); ++i){int children_i_depth = maxDepth(root->children[i]);depth = max(children_i_depth, depth) ; //注意，这里只找子树的最大高度}return depth+1; //深度是在子树最大高度的基础上加1}
};层序遍历解法：
class Solution {
public:int maxDepth(Node* root) {if(root == nullptr) return 0;int depth = 0;queue<Node *> que;que.push(root);while(!que.empty()){int size = que.size();++depth;for(int i = 0; i<size; i++){Node * node = que.front();que.pop();for(int j = 0;j < node->children.size();j++){if(node->children[j] != nullptr)que.push(node->children[j]);}} }return depth;}
};这篇关于算法练习第17天|104.二叉树的最大深度 、559.N叉树的最大深度的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
