基于R语言实现的beta二项回归模型【理解与实现】

本文主要是介绍基于R语言实现的beta二项回归模型【理解与实现】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本实验，创建一组使用二项分布模拟的数据（不带额外的随机性），和另一组使用Beta二项分布模拟的数据（引入了随机成功概率 p，从而增加了数据的离散性。

现在假设我们站在上帝视角，有两组不知道分布的数据。

一、如何理解：“观察到的方差大于二项分布预期的方差”

1.生成二项分布数据（不带额外的随机性）

set.seed(123)  # 确保结果可重现
n <- 100  # 样本大小
p_fixed <- 0.5  # 固定的成功概率
trials <- 100  # 每次试验的总次数# 生成数据
binomial_data <- rbinom(n, trials, p_fixed)

2. 生成Beta二项分布数据（引入随机性的成功概率）

# Beta分布参数
alpha <- 2
beta <- 5# 生成成功概率
p_random <- rbeta(n, alpha, beta)# 使用Beta生成的成功概率生成数据
beta_binomial_data <- rbinom(n, trials, p_random)

3. 计算并比较两组数据的方差

# 计算实际方差
var_binomial <- var(binomial_data)
var_beta_binomial <- var(beta_binomial_data)# 计算二项分布预期的方差
expected_var_binomial <- trials * p_fixed * (1 - p_fixed)# 打印结果
print(paste("方差 - 二项分布数据:", var_binomial))
print(paste("方差 - Beta二项分布数据:", var_beta_binomial))
print(paste("预期方差 - 标准二项分布:", expected_var_binomial))

你会发现Beta二项分布数据的方差通常会大于二项分布数据的方差，因为Beta二项分布引入的成功概率的随机性增加了数据的离散性。同时，你也会发现这个方差大于标准二项分布预期的方差，这正是我们需要使用Beta二项模型的原因。

4.可视化

# 加载必要的库
library(ggplot2)# 创建数据框
df <- data.frame(Data_Type = c(rep("Binomial", length(binomial_data)), rep("Beta-Binomial", length(beta_binomial_data))),Count = c(binomial_data, beta_binomial_data)
)# 绘制直方图
ggplot(df, aes(x = Count, fill = Data_Type)) +geom_histogram(position = "identity", alpha = 0.7, bins = 20) +labs(title = "Histogram of Binomial vs Beta-Binomial Data",x = "Count", y = "Frequency") +theme_minimal()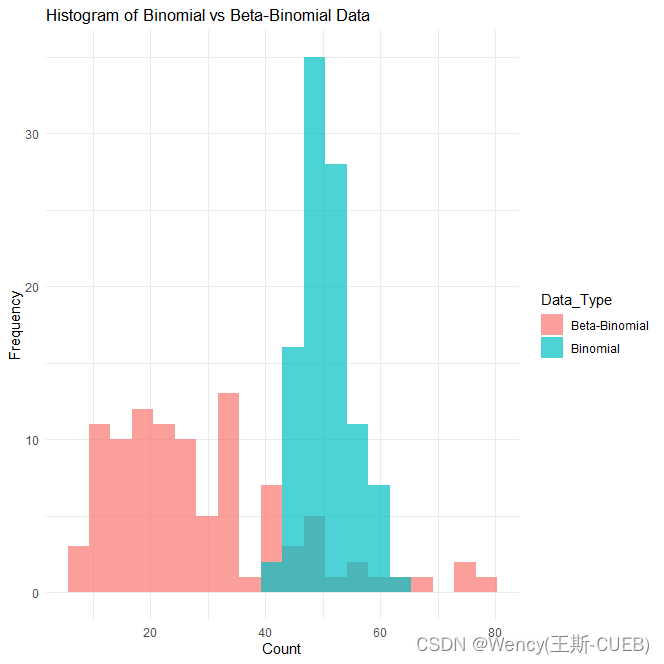

从直方图可以看出，Beta-Binomial 数据的分布更加广泛，呈现出更大的离散性，相比之下，Binomial 数据更加集中。这符合我们的预期，因为Beta-Binomial 数据引入了成功概率的随机性，增加了数据的变异性。

二、使用Beta二项分布模型主要涉及数据的拟合与分析过程

解释 VAGM

1.完整代码

# 加载必要的库
if (!require("VGAM")) install.packages("VGAM", dependencies = TRUE)
library(VGAM)# 生成模拟数据
set.seed(123)  # 设置随机数种子以确保结果可重现
n <- 100  # 样本大小
alpha <- 2  # Beta分布参数α
beta <- 5   # Beta分布参数β
trials <- sample(10:100, n, replace = TRUE)  # 每个观察的试验次数
p <- rbeta(n, alpha, beta)  # 从Beta分布生成成功概率
success <- rbinom(n, trials, p)  # 生成成功次数data <- data.frame(success = success, trials = trials, predictor1 = rnorm(n), predictor2 = runif(n))# 拟合Beta二项回归模型
model <- vglm(cbind(success, trials - success) ~ predictor1 + predictor2, family = betabinomial(link = "logit"), data = data)# 查看模型摘要
summary(model)# 模型诊断
par(mfrow = c(2, 2))
plot(model)# 模型预测
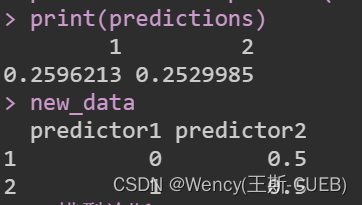
new_data <- data.frame(predictor1 = c(0, 1), predictor2 = c(0.5, 0.5))
predictions <- predict(model, newdata = new_data, type = "response")
print(predictions)

导出结果解释

1.数据的形式

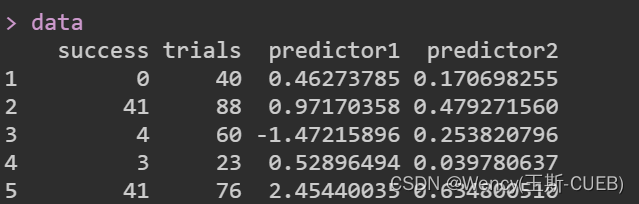
响应变量：成功次数和失败次数（Trials-success），
预测变量:predictor1 & predictor2

2.model 拟合结果

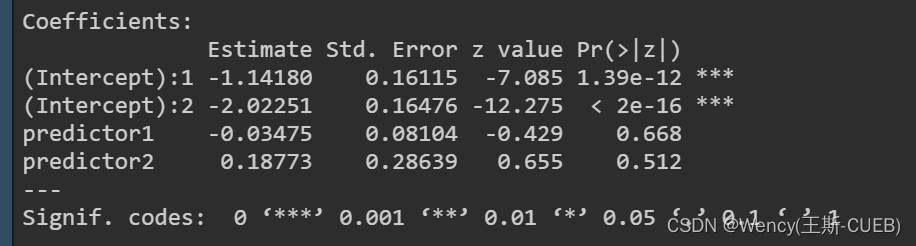
注意：
当我们拟合Beta二项分布时，模型实际上是在估计两个参数：成功概率p 的平均值和分布的离散程度。由于Beta分布是由两个参数控制的，这两个参数通常用不同的链接函数进行转换。
在这种情况下，每个链接函数可能有自己的截距，因此输出中显示了两个截距。

(Intercept):1 — 通常代表与成功概率 p 相关的截距项。
(Intercept):2 — 代表与Beta分布的离散参数相关的截距项。
忽略 参数的显著性

3.模型诊断

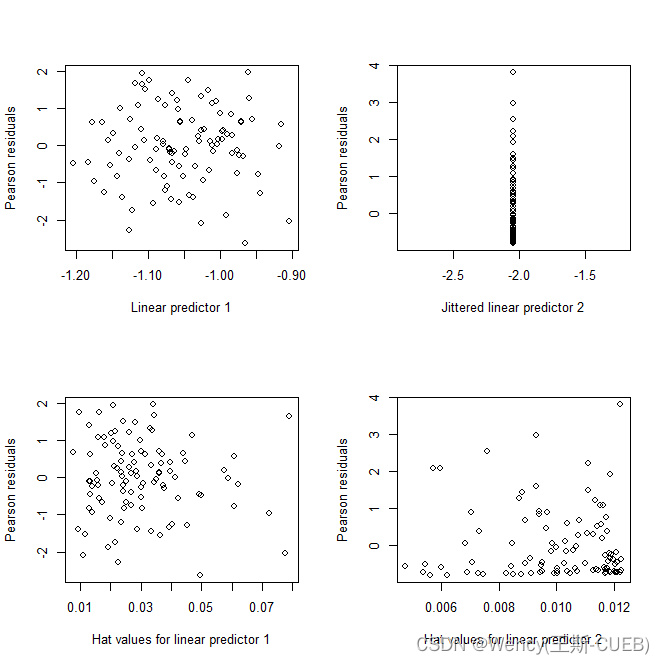
模型诊断图是统计建模中的一个重要组成部分，它们可以帮助我们识别模型中的问题，比如不符合假设的数据、异常值或模型拟合不良。
总体上：

从这些诊断图来看，模型似乎没有表现出明显的拟合问题。残差分布比较均匀，没有明显的模式，也没有迹象显示数据点有不适当的杠杆效应。
具体地：

• Pearson残差 vs. 线性预测器1：
  这个图显示了每个观测值的Pearson残差与第一个预测变量的线性预测值的关系。理想情况下，这些点应该随机分布，没有明显的模式。从图中看，残差似乎随着预测值的增加而稍微减小，但没有明显的趋势，。然而，这里没有强烈的模式或明显的异常值。

• Pearson残差 vs. Jittered线性预测器2：
  “Jittered”意味着在横轴的值上添加了一点随机噪声，以避免重叠点。这个图表应该类似于第一个图表，展示残差和第二个预测变量的关系。残差似乎在预测器2的中间范围内聚集得更紧密，这可能表明在这个范围内模型预测更准确。

• Pearson残差 vs. hat值（Linear Predictor 1）：
  帽子值（也称为杠杆值）度量了每个观测值对其自身预测值的影响程度。较高的hat值可能表明一个观测值具有较高的杠杆作用，可能是一个影响模型的异常值。图中hat值较高的点不多，意味着没有单个观测值对模型有过度影响。

• Pearson残差 vs. hat值（Linear Predictor 2）：
  这个图展示的是第二个预测变量的值。同样，我们希望没有观测值有过大的hat值。大多数观测值似乎有低到中等的hat值，没有迹象表明有单个观测对模型有过度影响。

模型预测

# 2.代码解释

解释代码
生成模拟数据：使用Beta分布参数 α=2 和 β=5 来模拟真实的成功概率 p。
为每个观察生成一个试验次数，并基于模拟的 p 生成成功次数。
拟合模型：
使用vglm函数从VGAM包拟合Beta二项模型，其中响应变量是成功和失败的次数，解释变量是predictor1和predictor2。
查看和解释模型摘要：
调用summary()函数来获取模型的详细输出，包括估计的参数和它们的统计显著性。
模型诊断：

使用plot()函数生成模型的诊断图，这有助于检查任何潜在的问题，如拟合不良或异常值。
模型预测：

对新的观察数据（在new_data中定义）进行预测，以展示模型如何应用于实际数据

这篇关于基于R语言实现的beta二项回归模型【理解与实现】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---