本文主要是介绍【算法篇】三道题理解算法思想——认识BFS,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
BFS(宽搜)
宽度优先遍历和深度优先遍历组成了大家熟悉的搜索算法,这两种算法也是蓝桥杯之类竞赛题的常考思想,正巧马上蓝桥杯临近,博主也是刷了很多BFS相关的题型,在这篇文章中会从力扣上选取三道简单的宽搜题型,带大家了解BFS的模板以及对他有个初步认识。
本篇文章题目较为简单,大家可以根据第一题的模板,自己先去力扣上做题然后回来看题解,稍后我们继续更新难度更高的宽搜题目,希望大家能给个关注👍。

文章顺序:
题目链接-》算法思路-》代码呈现。
算法摘要:
宽度优先遍历是一种利用队列这种数据结构,从某一点开始,一层一层进行遍历的一种算法思想,而BFS(宽搜)实际上就是一种暴力搜索算法,利用宽度优先遍历来查找想要结果。
1.N叉树的层序遍历
题目链接:
https://leetcode.cn/problems/n-ary-tree-level-order-traversal/description/

算法思路:
代码展示:
/*
// Definition for a Node.
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
*/class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> lists=new ArrayList<>();if(root==null){return lists;}Queue<Node> q=new LinkedList<Node>();q.add(root);while(!q.isEmpty()){int sz=q.size();List<Integer> list=new ArrayList<>();for(int i=0;i<sz;i++){Node cur=q.poll();list.add(cur.val);for(Node c:cur.children){if(c!=null){q.add(c);}}}lists.add(list);}return lists;}
}2.二叉树的最大宽度
题目链接:
https://leetcode.cn/problems/maximum-width-of-binary-tree/description/

算法思路:
代码展示:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int widthOfBinaryTree(TreeNode root) {if(root==null){return 0;}int max=1;Queue<Pair<TreeNode,Integer>> q=new LinkedList<>();q.add(new Pair(root,1));while(!q.isEmpty()){int sz=q.size();int head=0,last=0;for(int i=0;i<sz;i++){Pair<TreeNode,Integer> p=q.poll();TreeNode cur=p.getKey();int v=p.getValue();if(cur.left!=null){q.add(new Pair(cur.left,v*2));}if(cur.right!=null){q.add(new Pair(cur.right,v*2+1));}if(i==0){head=v;}if(i==(sz-1)){last=v;}}max=max>(last-head+1)?max:(last-head+1);}return max;}
}3.在每个树行中找最大值
题目链接:
515. 在每个树行中找最大值 - 力扣(LeetCode)
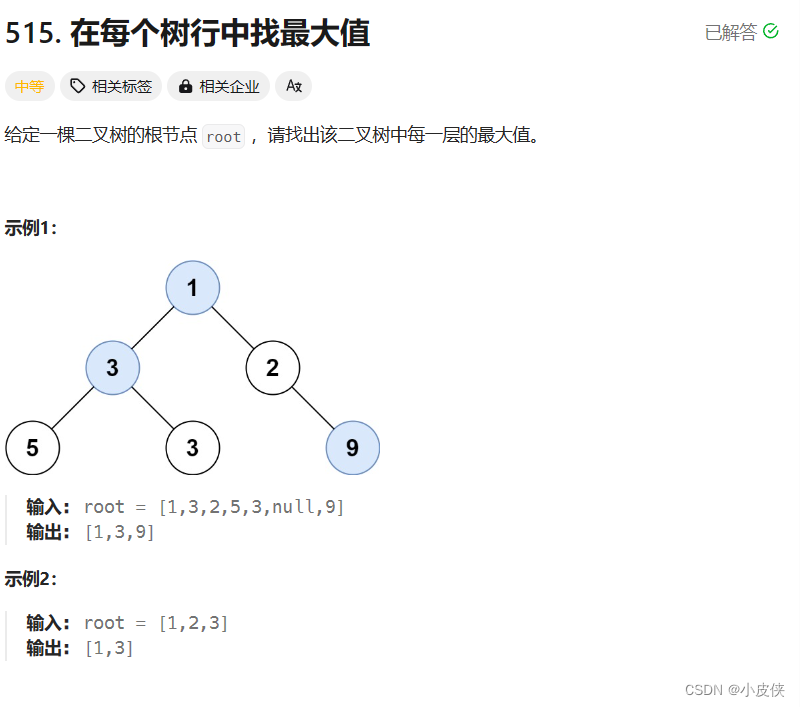
算法思路:
代码展示:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> largestValues(TreeNode root) {List<Integer> list=new ArrayList<>();if(root==null){return list;}Queue<TreeNode> q=new LinkedList<>();q.add(root);while(!q.isEmpty()){int sz=q.size();int max=Integer.MIN_VALUE;for(int i=0;i<sz;i++){TreeNode cur=q.poll();if(cur.left!=null){q.add(cur.left);}if(cur.right!=null){q.add(cur.right);}max=max>cur.val?max:cur.val;}list.add(max);}return list;}
}❤️😍😍😍😍😍😍😍😍😍😍😍😍😍😍😍😍😍
🍔我是小皮侠,谢谢大家都能看到这里!!
🦚主页已更新Java基础内容,数据结构基础,数据库,算法
🚕未来会更新Java项目,SpringBoot,Redis以及各种Java路线会用到的技术。
🎃求点赞!求收藏!求评论!求关注!
🤷♀️谢谢大家!!!!!!!!!
我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=2upjellgk3eow
这篇关于【算法篇】三道题理解算法思想——认识BFS的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





