本文主要是介绍算法打卡day25,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
今日任务:
1)491.递增子序列
2)46.全排列
3)47.全排列 II
491.递增子序列
题目链接:491. 非递减子序列 - 力扣(LeetCode)
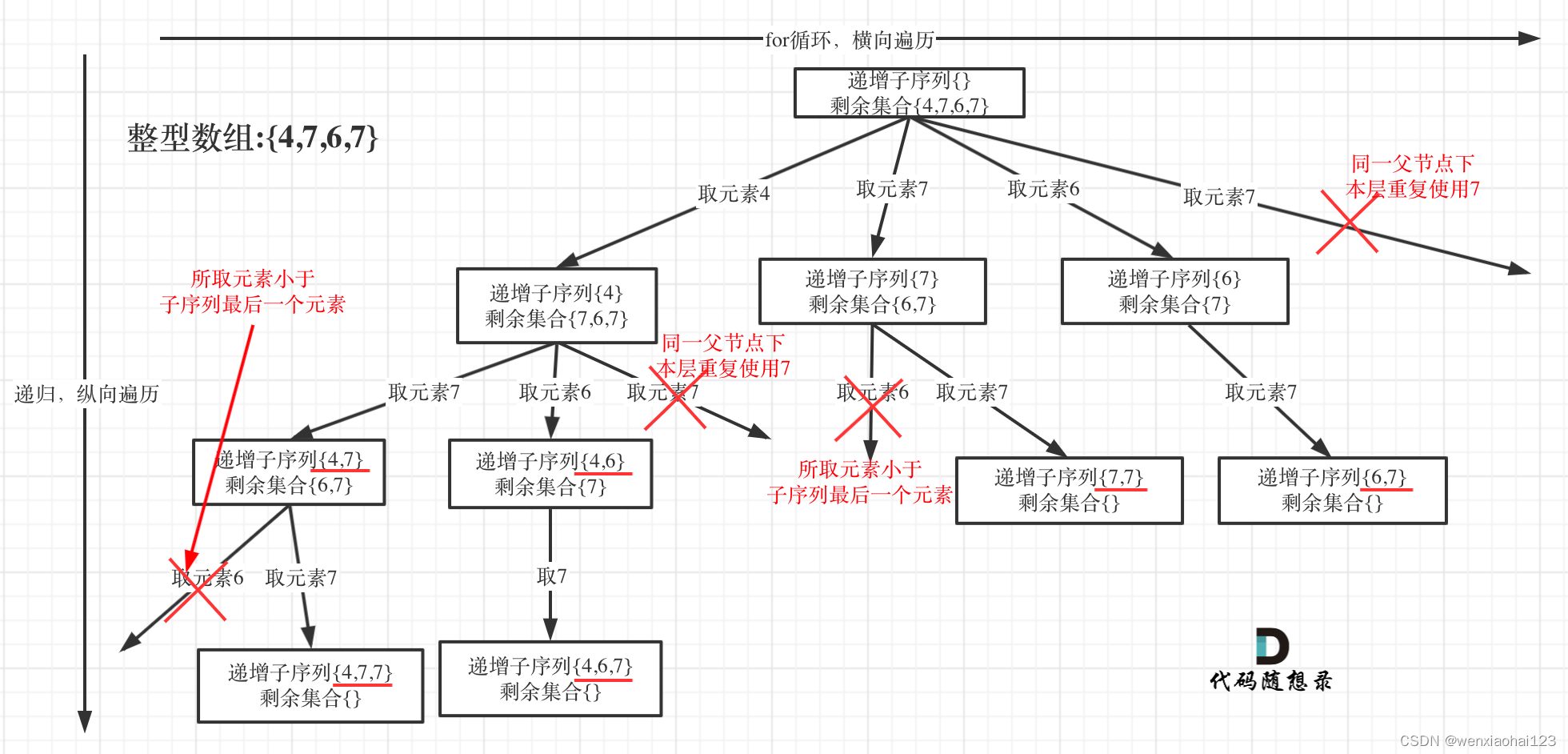
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
输入: [4, 6, 7, 7]
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]说明:
给定数组的长度不会超过15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况
文章讲解:代码随想录 (programmercarl.com)
视频讲解:回溯算法精讲,树层去重与树枝去重 | LeetCode:491.递增子序列哔哩哔哩bilibili
思路:
- 使用回溯算法,遍历数组中的每个元素。
- 对于当前元素,尝试将其加入当前子序列中,然后递归地向后探索更长的子序列。
- 在向后探索过程中,需要进行剪枝操作,以排除重复的结果和不满足递增条件的情况。
- 当遍历完所有可能的情况时,将满足要求的子序列加入结果列表中
下面是一个错误代码
class Solution:def findSubsequences(self, nums: List[int]) -> List[List[int]]:self.result = []self.backtrack(nums, 0, [])return self.resultdef backtrack(self, nums, start, path):# 如果当前路径长度大于1,则将该路径加入结果列表中if len(path) > 1:self.result.append(path[:])# 遍历数组中从start索引开始的所有元素for i in range(start, len(nums)):# 剪枝条件1:如果当前元素与前面的元素相同,则跳过,避免重复结果if i > start and nums[i] in nums[:i]:continue# 剪枝条件2:如果当前元素小于路径中的最后一个元素,跳过,确保生成的子序列是递增的if not path or nums[i] >= path[-1]:# 递归path.append(nums[i])self.backtrack(nums, i + 1, path)path.pop()
在第一个剪枝部分,不能直接去用当前nums[i]与数组之前的部分判断重复,这样是判断当前元素是否出现在路径中
这样导致的我们找的子集是没有重复元素的,但[1,2,1,1]这种是符合要求的,所以这样剪枝是错的
而是应该判断当前层,元素nums[i]是否遍历过

46.全排列
题目链接:46. 全排列 - 力扣(LeetCode)
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
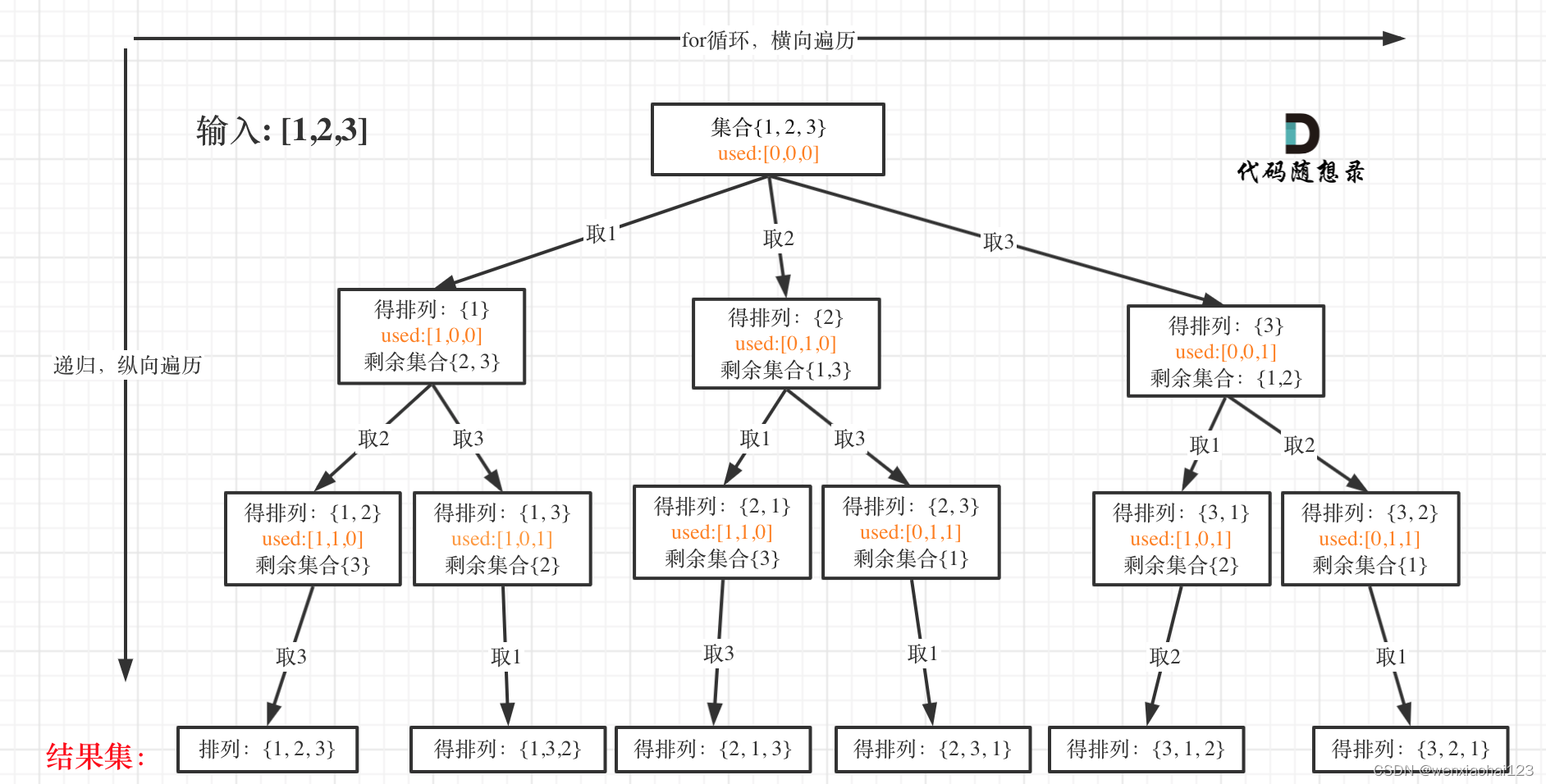
输入: [1,2,3]
输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
文章讲解:代码随想录 (programmercarl.com)
视频讲解:组合与排列的区别,回溯算法求解的时候,有何不同?| LeetCode:46.全排列哔哩哔哩bilibili
思路:
使用回溯算法来生成全排列。
维护一个结果列表 result 来存储所有可能的全排列。
回溯函数 backtrack 的参数包括当前要排列的数组 nums 和当前已生成的部分排列 path。
在回溯函数中,首先判断是否满足终止条件,即 path 的长度是否等于 nums 的长度,如果满足则将 path 加入 result 中。
然后遍历数组 nums 中的每个元素,如果该元素已经在 path 中,则跳过,否则将其加入 path 中,递归调用回溯函数,完成后需要撤销选择,以便尝试其他未选择的元素。
class Solution:def permute(self, nums: List[int]) -> List[List[int]]:self.result = []self.backtrack(nums, [])return self.resultdef backtrack(self, nums, path):# 当遍历完时,path长度等于原数组长度if len(path) == len(nums):self.result.append(path[:])for i in range(len(nums)):# 剪枝:如果当前元素已经遍历则跳过if nums[i] in path:continue# 递归层path.append(nums[i])self.backtrack(nums, path)path.pop()感想:
这题比较简单,递归遍历时,起始位置与之前的不一样,这次从头遍历
47.全排列 II
题目链接:47. 全排列 II - 力扣(LeetCode)
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
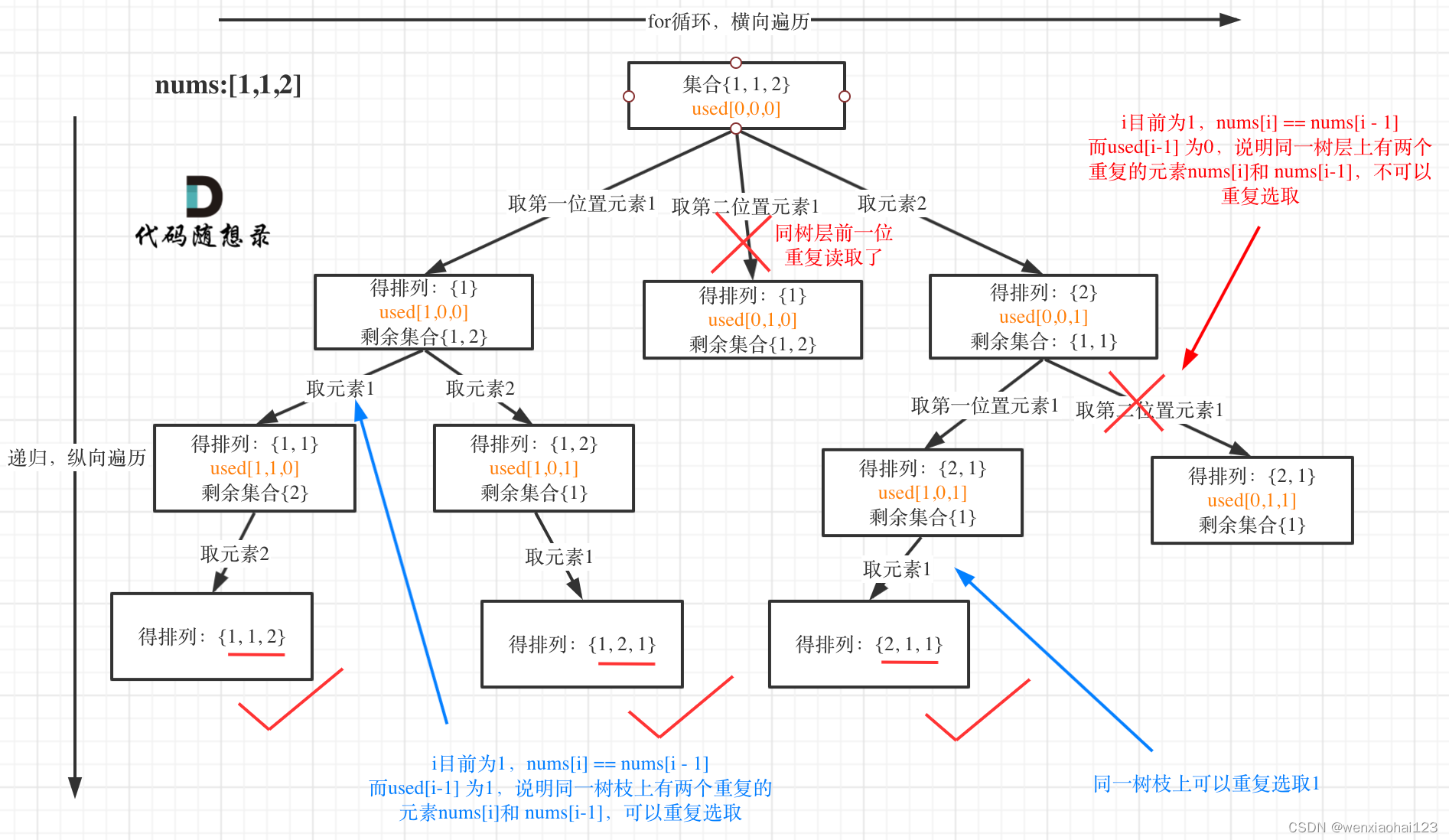
输入:nums = [1,1,2]
输出: [[1,1,2], [1,2,1], [2,1,1]]示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10
文章讲解:代码随想录 (programmercarl.com)
视频讲解:回溯算法求解全排列,如何去重?| LeetCode:47.全排列 II哔哩哔哩bilibili
思路:
1)使用回溯算法来生成全排列。
2)首先对原数组进行排序,这样重复元素会相邻,方便后续剪枝操作。
3)回溯函数 backtrack 的参数包括当前要排列的数组 nums、当前已生成的部分排列 path 和一个数组 used,用于记录每个数字是否已被使用。
4)在回溯函数中,首先判断是否满足终止条件,即 path 的长度是否等于 nums 的长度,如果满足则将 path 加入 result 中。
5)然后遍历数组 nums 中的每个元素,如果该元素已经被使用过,则跳过,否则标记该元素为已使用,选择当前元素并递归调用回溯函数,完成后需要撤销选择,并将当前元素标记为未使用,以便尝试其他未选择的元素。
class Solution:def permuteUnique(self, nums: List[int]) -> List[List[int]]:nums.sort()self.result = []self.backtrack(nums, [], [False] * len(nums))return self.resultdef backtrack(self, nums, path,used):# 终止条件:当路径长度等于原数组长度时,表示已经生成了一个全排列if len(path) == len(nums):self.result.append(path[:])for i in range(len(nums)):# 剪枝:如果当前元素已经遍历则跳过if used[i]:continue# 剪枝:同一层不能重复取相同的数字,若前一个相同数字未被使用,则跳过当前数字if i > 0 and nums[i] == nums[i - 1] and used[i-1] == False:continueused[i] = True # 标记当前元素已被使用# 递归层path.append(nums[i])self.backtrack(nums, path,used)path.pop()used[i] = False感想:
这一题有两个剪枝,第一个是每一个树层上,也就是同一级的for循环上,如果有重复的,我们就不用继续了,因为第一个元素出现时就已经涵盖所有可能性。我们可以对数组排序,然后比较当前nums[i]是否等于前一个,还需要补充的限制是,前一个已经遍历过了
第二个剪枝就是与上一题一样的,每一个树枝上已经使用的放进path中的就跳过
这篇关于算法打卡day25的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!