算法导论——24.3 Dijkstra最短路径算法java实现

本文主要是介绍算法导论——24.3 Dijkstra最短路径算法java实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

介绍

迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。
Dijkstra算法是典型的算法。 Dijkstra算法是很有代表性的算法。Dijkstra一般的表述通常有两种方式，一种用永久和临时标号方式，一种是用 OPEN, CLOSE表的方式，这里均采用永久和临时标号的方式。注意该算法要求图中不存在负权边。

适用条件&范围

1. 单源最短路径(从源点s到其它所有顶点v);

2.有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图);

3.边权非负;

4. 差分约束系统;

算法描述

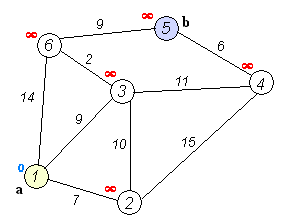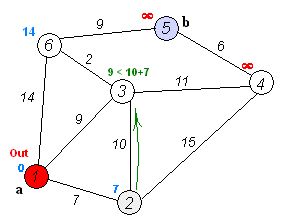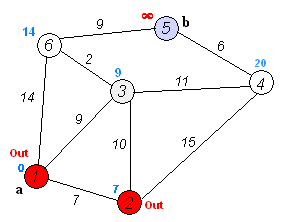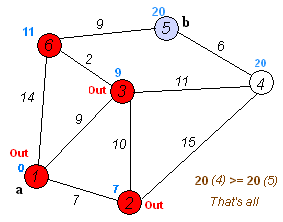
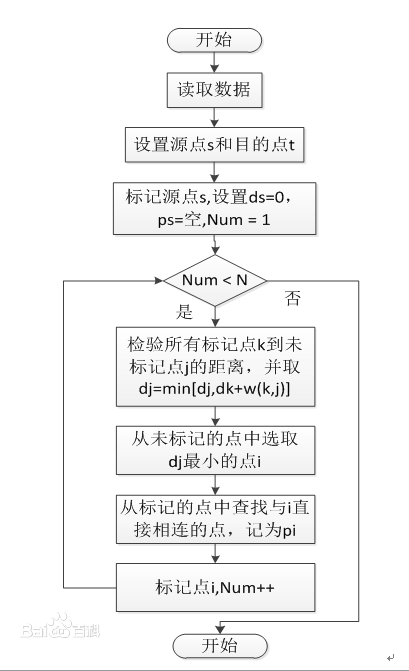
时间复杂度

邻接矩阵 O(n^2)
邻接表 O(n^2)
邻接表+binary heap O((n+m)logn)
邻接表+fibonacci heap O(m+nlogn)

Java代码实现

package algorithms;import util.AlgoGraph;import java.util.Stack;/*** Created with IntelliJ IDEA.* Created by The_Sam on 2017/5/8 22:08*/
public class Dijkstra extends ShortestAlgorithms {private Stack<Integer> Dealing ;private boolean Dealed[];public static void main(String[] args) {ShortestAlgorithms dk = new Dijkstra();System.out.println(dk.analyse(AlgoGraph.defaultMap4()));}boolean analyse(AlgoGraph algoGraph) {ini(algoGraph);int edgenum = algoGraph.getEdgenum();while (!Dealing.empty()) {int i=Dealing.pop();Dealed[i]=true;for (int j = 0; j < edgenum; j++) {//这里以枚举边的方式找以i为u的边，或许还有更好的做法，比如邻接表的形式int u = algoGraph.edge.get(j).u;if (i != u) continue;int v = algoGraph.edge.get(j).v;int cost = algoGraph.edge.get(j).cost;if (dis[v] > dis[u] + cost) {dis[v] = dis[u] + cost;pre[v] = u;if(!Dealed[v])Dealing.push(v);}}}return true;}void ini(AlgoGraph algoGraph) {int nodenum = algoGraph.getNodenum();//初始化，将dis[s]设为0，其他的都设为无限大dis = new int[nodenum];//dis[i] 为 i点到s的最短距离pre = new int[nodenum];//pre[i] 为i搭配s的最短距离的上一个节点Dealed =new boolean[nodenum];Dealing=new Stack<Integer>();int s = algoGraph.getOriginal();//原点Dealing.push(s);for (int i = 0; i < nodenum; i++) {dis[i] = i == s ? 0 : MAXN;}}
}

AlgoGraph.java 表示图的代码附上
package util;import lombok.Getter;
import lombok.Setter;import java.util.ArrayList;/*** Created by The_Sam on 2017/5/8.* 图是从0到nodenum-1表示相应节点*/
public class AlgoGraph {@Getter@Setterprivate int original;@Getter@Setterprivate int nodenum;private int indegrees[];//    private int indegrees[];//indegree[i]表示i节点的入度public ArrayList<AlgoEdge> edge;public int getEdgenum() {return edge.size();}public AlgoGraph(int original, int nodenum, ArrayList<AlgoEdge> edge) {this.original = original;this.nodenum = nodenum;this.edge = edge;}/*** @Description :返回函数各个节点的入度* @Author : The_Sam* @Datetime : 2017/5/8 23:04* @Params :* @Return : int[]*/public int[] getIndegrees() {indegrees=new int[nodenum];for (AlgoEdge e :edge) {indegrees[e.v]++;}return indegrees;}/*** @Description: 返回一个图，为算法导论图24-4，带负权无负权回路有向环图* @Author: The_Sam* @Datetime: 2017/5/8 21:22* @Params: []* @Return: AlgoGraph*/static public AlgoGraph defaultMap1() {ArrayList<AlgoEdge> edge = new ArrayList<AlgoEdge>();edge.add(new AlgoEdge(0, 1, 6));edge.add(new AlgoEdge(0, 2, 7));edge.add(new AlgoEdge(1, 2, 8));edge.add(new AlgoEdge(1, 3, 5));edge.add(new AlgoEdge(1, 4, -4));edge.add(new AlgoEdge(2, 3, -3));edge.add(new AlgoEdge(2, 4, 9));edge.add(new AlgoEdge(3, 1, -2));edge.add(new AlgoEdge(4, 0, 2));edge.add(new AlgoEdge(4, 3, 7));int original = 0;int nodenum = 5;return new AlgoGraph(original, nodenum, edge);}/*** @Description: 返回一个图，为算法导论图24-4改变版，有负权回路有向环图* @Author: The_Sam* @Datetime: 2017/5/8 21:22* @Params: []* @Return: AlgoGraph*/static public AlgoGraph defaultMap2() {ArrayList<AlgoEdge> edge = new ArrayList<AlgoEdge>();edge.add(new AlgoEdge(0, 1, 6));edge.add(new AlgoEdge(0, 2, 7));edge.add(new AlgoEdge(1, 2, 8));edge.add(new AlgoEdge(1, 3, 5));edge.add(new AlgoEdge(1, 4, -4));edge.add(new AlgoEdge(2, 3, -3));edge.add(new AlgoEdge(2, 4, 9));edge.add(new AlgoEdge(3, 1, -2));edge.add(new AlgoEdge(4, 0, 2));edge.add(new AlgoEdge(4, 3, 5));//此处改变 edge.add(new AlgoEdge(4, 3, 7));int original = 0;int nodenum = 5;return new AlgoGraph(original, nodenum, edge);}/*** @Description: 返回一个图，为算法导论图24-4改变版，有向无环图* @Author: The_Sam* @Datetime: 2017/5/8 21:22* @Params: []* @Return: AlgoGraph*/static public AlgoGraph defaultMap3() {ArrayList<AlgoEdge> edge = new ArrayList<AlgoEdge>();edge.add(new AlgoEdge(0, 1, 6));edge.add(new AlgoEdge(0, 2, 7));edge.add(new AlgoEdge(1, 2, 8));edge.add(new AlgoEdge(1, 3, 5));edge.add(new AlgoEdge(1, 4, -4));edge.add(new AlgoEdge(2, 3, -3));edge.add(new AlgoEdge(2, 4, 9));//edge.add(new AlgoEdge(3, 1, -2));//edge.add(new AlgoEdge(4, 0, 2));//edge.add(new AlgoEdge(4, 3, 5));//此处改变 edge.add(new AlgoEdge(4, 3, 7));int original = 0;int nodenum = 5;return new AlgoGraph(original, nodenum, edge);}/*** @Description: 返回一个图，为算法导论图24-4改变版，无负权有向环图* @Author: The_Sam* @Datetime: 2017/5/8 21:22* @Params: []* @Return: AlgoGraph*/static public AlgoGraph defaultMap4() {ArrayList<AlgoEdge> edge = new ArrayList<AlgoEdge>();edge.add(new AlgoEdge(0, 1, 6));edge.add(new AlgoEdge(0, 2, 7));edge.add(new AlgoEdge(1, 2, 8));edge.add(new AlgoEdge(1, 3, 5));edge.add(new AlgoEdge(1, 4, 4));edge.add(new AlgoEdge(2, 3, 3));edge.add(new AlgoEdge(2, 4, 9));//edge.add(new AlgoEdge(3, 1, -2));//edge.add(new AlgoEdge(4, 0, 2));//edge.add(new AlgoEdge(4, 3, 5));//此处改变 edge.add(new AlgoEdge(4, 3, 7));int original = 0;int nodenum = 5;return new AlgoGraph(original, nodenum, edge);}
}

AlgoEdge.java表示边的代码附上
package util;/*** Created by The_Sam on 2017/5/8.*/
public class AlgoEdge {public int u,v;public int cost;public AlgoEdge(int u, int v, int cost) {this.u = u;this.v = v;this.cost = cost;}
}

这篇关于算法导论——24.3 Dijkstra最短路径算法java实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！