量子近似优化算法(QAOA)入门（1）：从量子绝热算法(QAA)角度的直观理解

前言：量子计算的本质是测量

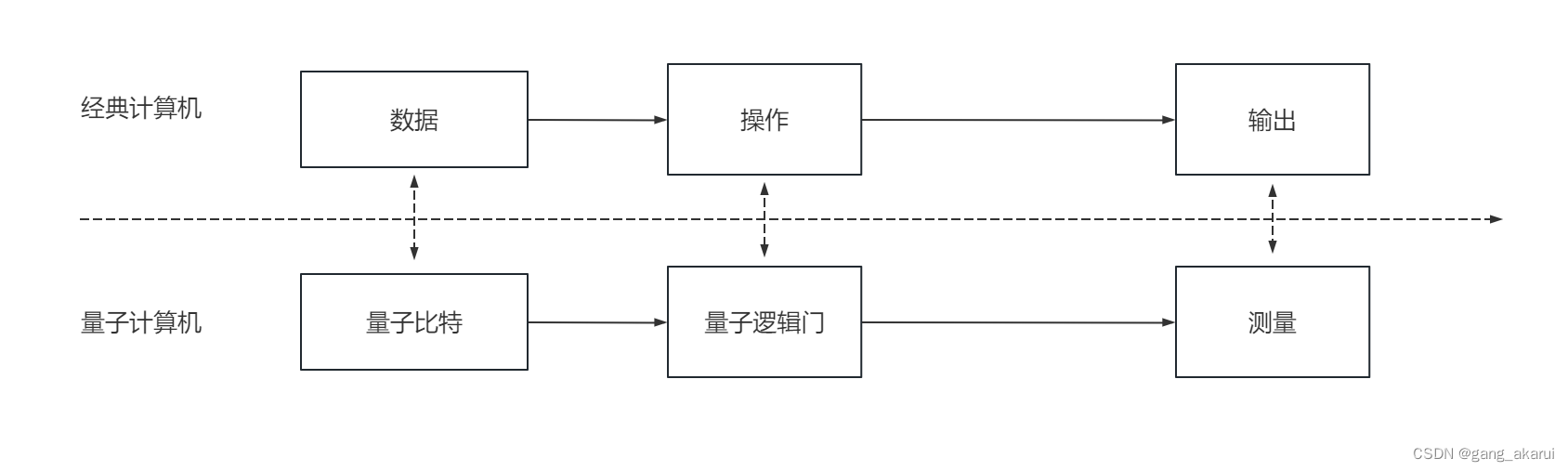
开始大家要有这样一个认识，才不会在学习过程中困惑。

一、基于量子逻辑电路的常用算法

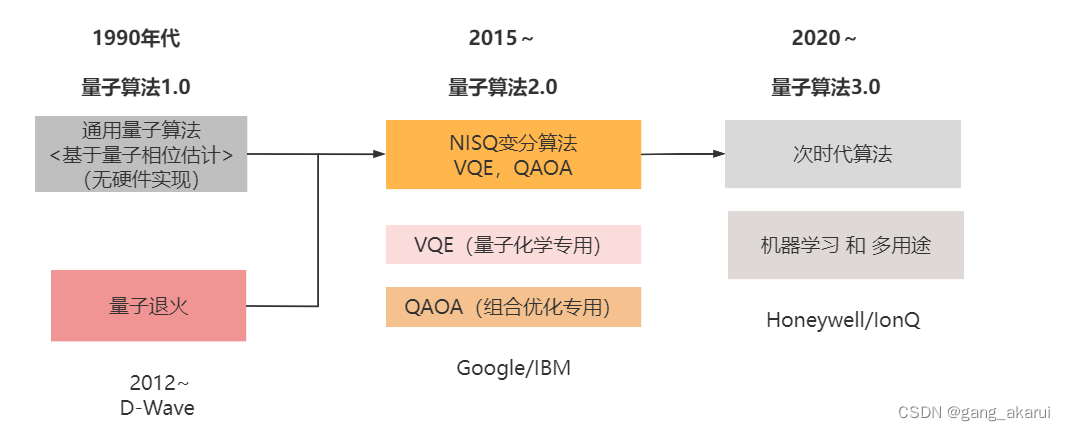
• VQE : Variational Quantum Eigensolver
• QAOA : Quantum Approximate Optimization Algorithm

1.NISQ：Noisy Intermediate-Scale Quantum（含噪声中等规模量子）

这个词是不能单独理解，我们先理解【NISQ设备：Noisy Intermediate-Scale Quantum device】是什么。

NISQ设备，指数年或数十年可以实现的，小～中规模（包含数个～数百个量子比特）的量子计算机。NISQ设备在计算过程中容易受到噪声影响，而且不能纠错，所以计算结果容易出现的错误。比如著名的量子算法Shor算法和Grover算法，电路复杂（运算较多），NISQ设备容错性低，很难实现这俩算法。 我们离真正的可以在计算中即时纠错的量子计算机还很远。

在此背景下，“量子-经典混合算法”的方法成为NISQ算法研究的主流。这意味着我们不是将我们要执行的所有计算都委托给量子计算机，而是只将量子计算机擅长的部分委托给量子计算机，让经典计算机处理其余部分。这个思想也是QAOA的基本思想。

所以，QAOA不是纯粹的基于量子逻辑门的算法，有部分计算是经典计算机完成的。
主要的参考论文是下面两篇。

• 该文首次提出QAOA算法

A Quantum Approximate Optimization Algorithm
https://arxiv.org/pdf/1411.4028.pdf

• 该文是Rigetti公司的通过量子逻辑电路实现QAOA算法的报告论文

Unsupervised Machine Learning on a Hybrid Quantum Computer
https://arxiv.org/pdf/1712.05771.pdf

二、量子绝热算法（QAA：Quantum Adiabatic Algorithm）

1.QAA的原理

这章主要参考以下文章：

https://qiita.com/snhrhdt/items/ae55a94b25c06142528a

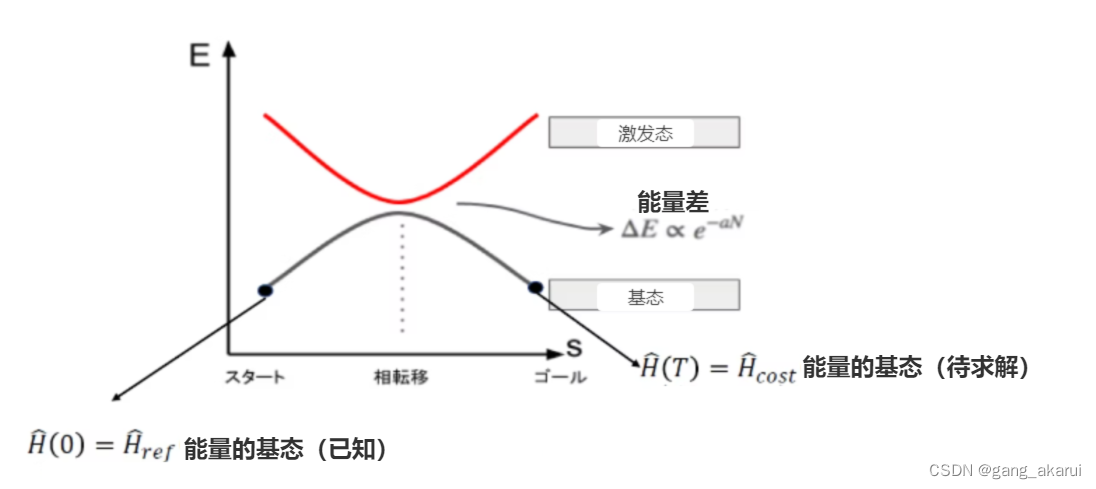
QAA的思想很简单，就是把待求解的哈密顿量，映射到一个基态已知的能量体系。然后，通过量子绝热演化，就能获得待求解的哈密顿量基态。计算式如下：

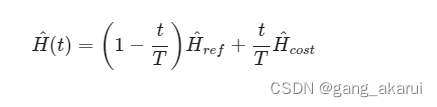
量子绝热演化的过程就是，极其缓慢地令t：0→T

• t = 0 时
  

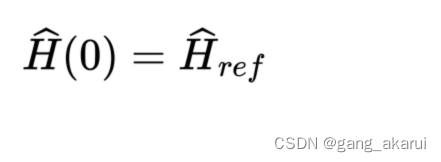
• t = T 时
  
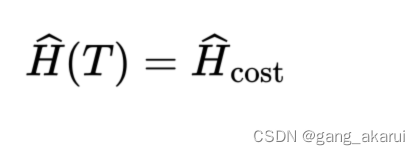
  QAA背后的想法是从一个简单的哈密顿量开始，我们可以很容易地获得并准备好基态，并“小心”地演化。演化过程中该哈密顿量一直保持在基态，直到它的哈密顿量的基态是我们问题的解。

这篇文章的目的是直觉上理解量子绝热算法。并且阐明怎么通过魔改QAA，从而发明了QAOA。具体的物理推导，之后的篇章再说。

2.量子绝热算法和量子退火算法的区别

量子退火算法依赖于与绝热量子计算相同的核心思想：它采用一个初始哈密顿量$H_0$，一个终态哈密顿量$H_1$，其基态编码就是求解问题的解。

但是量子退火算法和QAA有两个不同点。

• 终态$H_1$能够实现的哈密顿量不能完全随意选择，而必须从某个限定的类中选择。一个典型的选择是形式的以下的伊辛哈密顿量。
  
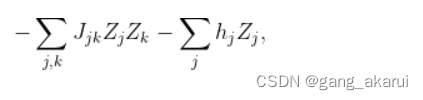
• 在量子退火中，进化不再保证是绝热的。做出这个决定有两个主要原因。
  第一个原因：上面图中的光谱间隙是$H(t)$,$t\in [0,T]$ 的基态与第一激发态之差的最小值。计算这个光谱间隙是非常困难的。
  第二个原因：即使我们能够计算出绝热过程所需的时间，它也可能时间太久以至于不实用——甚至不可能，我们等不及。

所以，量子退火选择了妥协。

三、量子近似优化算法（QAOA : Quantum Approximate Optimization Algorithm）

• 量子退火算法，挺好用了，为啥要发明QAOA呢？
  因为，量子逻辑电路，只能以离散的步骤改变状态向量。就如下面的量子逻辑电路图一样。

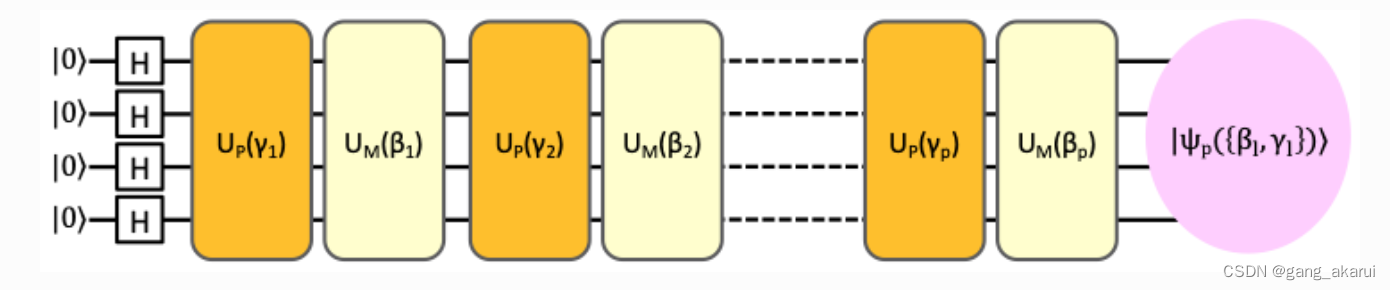
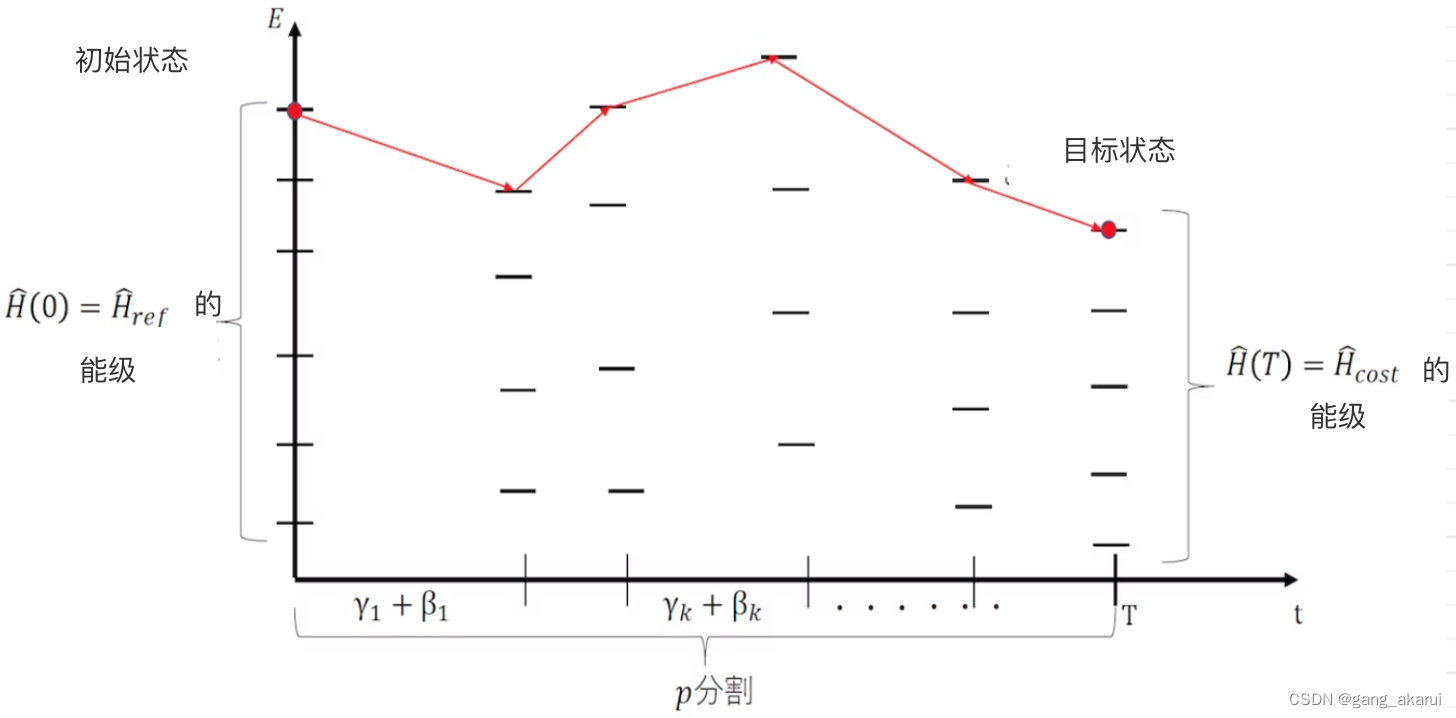
更直观的理解就是，把时间 $t$ 上的演化，通过p个逻辑电路进行模拟。那么p越大，就越接近于量子退火的连续时间演化了。这里有三个参数γ、β、p。大家应该可以理解对应关系，至于细节，放到之后的文章里讲解。

下图的参考链接：https://qiita.com/snhrhdt/items/ae55a94b25c06142528a

总结

这篇文章，理清了QAOA的发明过程，以及直观理解，没有使用公式，之后慢慢代入公式进行讲解。