【通信原理 入坑之路】—— 信息论部分 线性分组码各种计算的解法

在开始本文之前，我们先给出下面的几个名词，他们将会在后续的分析中反复出现：
【1】生成矩阵 【2】监督矩阵 【3】许用码字 【4】最小汉明距离 【5】伴随式 【6】错误图样

我们先重点看看接收端中，上面这些名词的关联：

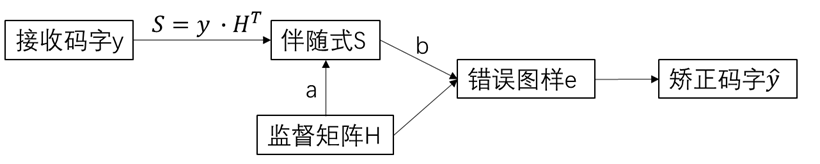
首先，当我们接收到码字 y 时，我们可以通过监督矩阵计算出伴随式 S，通过伴随式，我们又可以得到错误图样，错误图样的意义就是它能够指出接收码字中哪一位出错了。从而去修改对应位置的码字。【监督矩阵的监督作用可以通过 ：$H\cdot C^T=0$表现出来】

下面我们具体看看如何通过监督矩阵得到所有的伴随式，也就是过程 a：

1. 假设我们现在计算得到了监督矩阵H：$$H=\left[\begin{array}{ccccccc}1& 1& 0& 1& 0& 0& 0\\ 0& 1& 1& 0& 1& 0& 0\\ 1& 1& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 0& 0& 1\end{array}\right]$$
   那么伴随式S就是H 矩阵各列的组合（异或运算）。比如说，我们现在选择H的第1，2列进行异或，就会得到其中一个伴随式：$S=\left[\begin{array}{cccc}0& 1& 0& 1\end{array}\right]$；再比如说我们如果只选择H的第6列进行异或，也可以得到另一个伴随式：$S=\left[\begin{array}{cccc}0& 0& 1& 0\end{array}\right]$

下面我们具体看看如何通过伴随式求出错误图样，以及如果通过错误图样反推伴随式：

1. 如何通过伴随式求出错误图样？结果可能是不唯一的。由于我们刚刚不是选取了H的第1，2列异或得到了一个伴随式：$S=\left[\begin{array}{cccc}0& 1& 0& 1\end{array}\right]$吗，所以上图的 b 过程就是说你伴随式S是选取了H的哪些列计算得到了，那么错误图样 e 就是在对应的位置标记为“1”，否则标记为“0”。所以，这个伴随式对应的错误图样就是 $\left[\begin{array}{ccccccc}1& 1& 0& 0& 0& 0& 0\end{array}\right]$，但是还有一种可能性：$S=\left[\begin{array}{cccc}0& 1& 0& 1\end{array}\right]$也可以是H矩阵的第5，7两列的组合。因此，错误图样还可能是：$\left[\begin{array}{ccccccc}0& 0& 0& 0& 1& 0& 1\end{array}\right]$

2. 而反过来通过错误图样找S，结果就是唯一的了。比如说错误图样：$\left[\begin{array}{ccccccc}1& 1& 0& 0& 0& 0& 0\end{array}\right]$，那么对应的伴随矩阵就只能是$S=\left[\begin{array}{cccc}0& 1& 0& 1\end{array}\right]$

而可纠正的错误图样，指的就是错误最少的那种情况。

说了那么多，那么生成矩阵和监督矩阵到底怎么求呢？我们记住下面的关系：$$Q=\left[\begin{array}{c}I|P\end{array}\right]$$
$$H=\left[\begin{array}{c}{P}^T|I\end{array}\right]$$

上述都是系统的生成矩阵和监督矩阵，如果题目给出来的矩阵不是系统的（也就是没有单位矩阵的），那么大部分情况可以通过行的互换得出。

求出了监督矩阵，我们就来看看最小汉明距离 $d_{min}$ 如何计算。其实 $d_{min}$ 就是看H矩阵中最少有多少列是线性相关的。还是以刚刚的H为例：
$$H=\left[\begin{array}{ccccccc}1& 1& 0& 1& 0& 0& 0\\ 0& 1& 1& 0& 1& 0& 0\\ 1& 1& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 0& 0& 1\end{array}\right]$$

我们发现，任意的3列都无法表示成线性关系，但是其中第5，6，7列的和恰好等于第3列，也就是说最少4列是可以表示成线性相关的，所以 $d_{min}=4$

我们再来看看许用码字的求法：

我们通过 (n, k) 码的形式【即：n位的码字里面有k个信息位】那么我们就把k个信息位的所有组合都列出来，然后分别跟生成矩阵相乘，就可以得到许用码字 $C$了。

其中，我们也可以通过生成矩阵的维度确定 n, k：生成矩阵的维度：(k, n).

另外还有一种题型：

已知某线性分组码的码长为 $10$，如果要想该线性码能够纠正两位随机错误，问需要多少位的监督位？

首先，我们明确这样一个性质：监督位如果有 $x$ 位，那么其伴随式就会有：$2^x$种。下面我们回到题目：题目说想要线性码能够纠正两位随机错误，这个随机错误其实就是通过错误图样来反应的。比如一个 $(7,4)$ 码，如果错误图样是 $[0001000]$，那么就可以判断是第四位出错了。

接下来我们看一下如果是出现两位错误的时候，错误图样有多少种情况：根据排列组合的知识，从10位里面选出2位作为错误位，那么有：$C_{10}^2=45$种情况。然后只错一位的情况一共有：$C_{10}^1=10$种。因此，错两位及以下的错误图样一共有：$45+10=55$种情况。那么因此，我们所选取的监督位就应该使得线性码所产生的错误图样数比55大。由于 $2^6=64>55>2^5=32$，因此，监督位的个数应该是6.