本文主要是介绍Consecutive Factors(求最大连续因数序列),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述 Among all the factors of a positive integer N, there may exist
several consecutive numbers. For example, 630 can be factored as
356*7, where 5, 6, and 7 are the three consecutive numbers. Now
given any positive N, you are supposed to find the maximum number of
consecutive factors, and list the smallest sequence of the consecutive
factors.
输入描述: Each input file contains one test case, which gives the integer
N (131).
输出描述: For each test case, print in the first line the maximum number
of consecutive factors. Then in the second line, print the smallest
sequence of the consecutive factors in the format
“factor[1]factor[2]…*factor[k]”, where the factors are listed in
increasing order, and 1 is NOT included.
输入例子: 630
输出例子: 3 567
PAT上的一个题,给定一个数N,要求这个数的最长连续因数,如果答案不唯一则取最小的因数序列(比如给了30,则有2*3和5*6,结果取5*6)并且1不计算在结果序列里面。
设结果序列中最小值为i,当i=sqrt(N)的时候,这个序列的最大长度为1(sqrt(N)*(sqrt*(N)+1)>N),可知i不会大于sqrt(N)。因此我们只需要令i=[2,sqrt(N)] ,依次寻找由i打头的最大序列并且记录即可。并且由于题目中要求的是不同答案中取i最小的那个序列,所以每次要当新的序列长度>max_len的时候才更新记录。
要注意的一点是,如果由2到sqrt(N)都找不到一个长度至少为1的序列,那么就说明这个数是个素数,那么这个序列应该为N本身,长度为1(1不包括在序列里)。
#include <iostream>
#include<math.h>
using namespace std;int main() {int N;cin >> N;int j = sqrt(N) + 1, max_len = 0, idx = -1;for (int i = 2; i < j; i++) {if (N % i != 0) continue;int t_len = 0, t_N = N,t_idx=i;while (t_N && t_N % t_idx == 0) {t_N /= t_idx;t_idx++,t_len++;}//这里>不能改成>=if ( t_len > max_len) {max_len = t_len;idx = t_idx-t_len;}}//找不到则序列为N本身if (idx == -1) {idx = N;max_len = 1;}cout << max_len << endl;for (int i = idx; i < idx + max_len; i++) {cout << i << ((i == idx + max_len - 1) ? "" : "*");}}
测试结果:
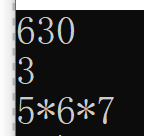
值得一提的是,这个算法的复杂度跟所给定整数的长度有关系,题目给的是int,占32位,最大值为2^31-1=2147483647,而12!=479 001 600,13!=6 227020800,既12!<intMax<13!,因此max_len的最大值不会超过11。并且由于是阶乘增长,随着i的变大max_len的最大值是会变小的,所以实际上平均下来max_len的最大值应该是比11小的。因此时间开销应该<11*sqrt(N)∈O(sqrt(N))
这篇关于Consecutive Factors(求最大连续因数序列)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






