本文主要是介绍数据结构之红黑树(二)——插入操作,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
插入或删除操作,都有可能改变红黑树的平衡性,利用颜色变化与旋转这两大法宝就可应对所有情况,将不平衡的红黑树变为平衡的红黑树。
在进行颜色变化或旋转的时候,往往要涉及祖孙三代节点:X表示操作的基准节点,P代表X的父节点,G代表X的父节点的父节点。
我们先来大体预览一下插入的过程:
1、沿着树查找插入点,如果查找过程中发现某个黑色节点的两个子节点都是红色,则执行一次颜色变换(父节点变为红色,而两个红色子节点变为黑色)。
2、第1步中,不会改变子树的黑色高度,但是可能会出现颜色冲突(红-红颜色冲突),执行一次或两次旋转即可解决。设红色子节点为X,红色父节点为P,旋转次数由X是G的内侧子孙还是外侧子孙决定。
3、找到插入点之后,设X为新插入的节点。如果P是黑色的,则不需要做任何改变,插入完成。
4、如果P是红色的,则发生了红-红颜色冲突,需要做两次颜色变化,如果X为G的外侧子孙,再进行一次旋转;如果X为G的内侧子孙,再进行两次旋转。最终都可使树变为平衡的红黑树。
现在看不懂没关系,为何要这么做,我们接下来慢慢分析。
第1步与第2步看似与插入新节点没关系,其实为了给新节点的插入扫清道路,到后面插入新节点时就会体现出来。
先来看第1步的详细过程:
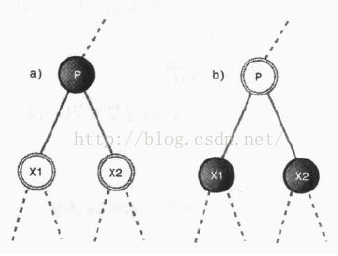
上图中,查找到P点,发现它的两个子节点都是红色,则进行颜色变换(如果P是根,则保持黑色不变)。这种变换并不会改变从根节点经P到叶节点或者空节点的路径上的黑色节点总数,即不会改变其黑色高度。将P、X1、X2看做三角形的三个顶点,颜色变换之前,经过此三角形时会增加一个黑色节点,颜色变换之后,P变成了红色,X1、X2变成了黑色,不论是经过X1还是经过X2,还是会增加一个黑色节点。
如果P的父节点是黑色,则不会出现任何问题,但是,如果P的父节点也是红色,就会发生红-红颜色冲突,需要通过旋转来修正。发生颜色冲突时有两种情况需要区别对待。
注意,这时候我们选定红-红颜色冲突父子节点中的子节点作为基准节点,即X。如果X在P的一侧与P在G的一侧相同,X即为G的外侧子孙,反之,则为内侧子孙。
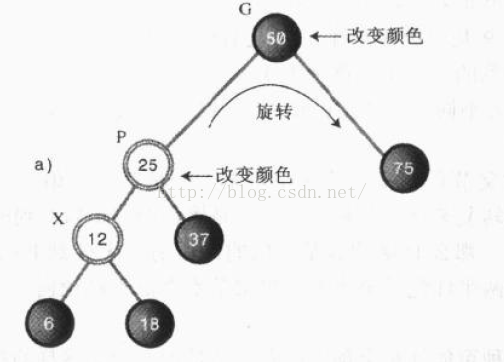
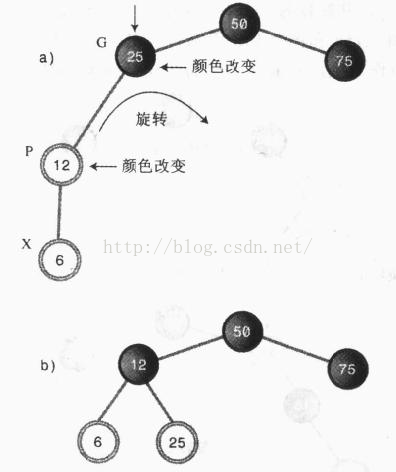
情况1:X为外侧子孙节点。
上图中,表示的是颜色变换之后的情况,12跟25节点发生了颜色冲突,12为50的外侧子孙。
在这种情况需要采取三步操作:
1、改变G的颜色;
2、改变P的颜色
3、以G为中心进行向X上升的方向旋转(本例中是右旋)。
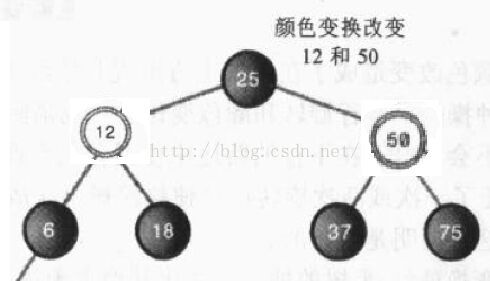
奇迹发生了,树突然之间平衡了,而且是符合红黑规则的。
需要注意的是,在本例中,由于25是50的左子节点,进行的是右旋操作,加入它是右子节点,则需要进行左旋操作。无论是左旋还是右旋,都是向着X上升的方向旋转。
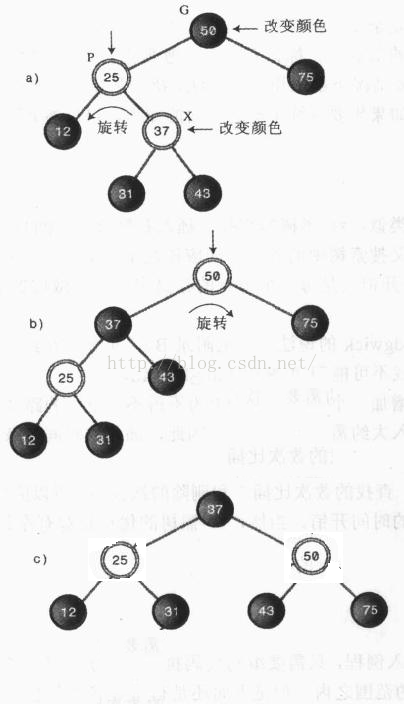
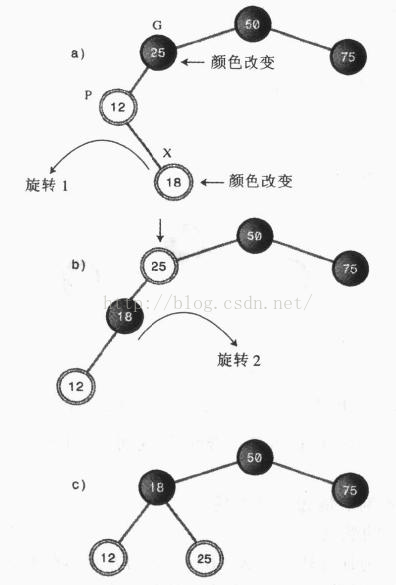
情况2:X为内侧子孙节点。
修正这种情况比较复杂一点,如果我们采取跟内侧子孙一样的做法,X不会上移而是发生横向移动,使树变得更加不平衡。因此需要一种不同的方法来解决。
我们先要用一次旋转让X成为外侧子孙,然后再用一次旋转使树平衡。
这种情况需要进行四步操作:
1、改变G的颜色;
2、改变X的颜色;
3、以P为中心向X上升的方向旋转;
4、以G为中心向X上升的方向旋转。
至此,前期工作已经完成,下面进行新节点的插入。在插入环节,我们以新节点为基准点,即X。
在前面已经说过,我们总是默认新节点为红色。那么,找到插入点的时候,会有两种情况,一种是X的父节点为P为黑色,直接插入即可(因为插入一个红色新节点既不会影响树的黑色高度,也不会发生颜色冲突);另一种情况是X的父节点P也为红色,插入后会发生红-红颜色冲突,需要通过颜色变换与旋转来修正。
发生颜色冲突的时候,根据X是内侧子孙还是外侧子孙分别对待,处理方法与上面提到的方法类似。
外侧子孙:
内侧子孙:
下面我们来讨论一下,是否还有其他情况。
假如X有一个兄弟节点S,即P的另一个子节点,会使任何需要的旋转更加复杂。如果P为黑色,无论X有没有兄弟节点,都不需要旋转;如果P为红色,则插入之前,P不可能有一个单独的黑色子节点,因为这样会使S和空子节点的黑色高度不一样。综上,插入新节点之后,不会出现X存在兄弟节点而且需要旋转修正的情况。
假如P有一个兄弟节点,即X的叔节点U,也会使任何需要的旋转更加复杂。如果P为黑色,X插入后不要要做任何旋转;如果P为红色,则U必须为红色,否则,G到P的黑色高度与G到U的黑色高度就不同了。但是,有两个红色子节点的父节点在插入之前我们已经处理掉了,所以这种情况也不会存在。综上,插入新节点之后,不会出现P存在兄弟节点且需要旋转修正的情况。
到现在,就明白为什么要在寻找插入点的过程中,把有两个红色子节点的父节点的颜色变换掉,一方面是为了使树更加平衡,另一方面是大大简化了插入后的旋转操作。
这篇关于数据结构之红黑树(二)——插入操作的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!