本文主要是介绍《三体》二向箔的降维打击——PCA算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在刘慈欣的《三体》中,歌者文明在2403年向太阳系投掷了二向箔,同年太阳系和大多数地球人被二维化而灭亡。那么究竟是如何实现的降维呢?接下来介绍一个算法——pca算法
B站的一位up主讲得很好,言简意赅:
主成分分析(PCA)的原理和简单推导_哔哩哔哩_bilibili
PCA是一种常用的数据降维技术,用于减少高维数据集的维度,同时保留数据中最重要的信息。它通过寻找数据中的主成分,将原始特征转换为新的一组互相不相关的变量,这些变量称为主成分。主成分按照方差的大小排序,前几个主成分所包含的方差越大,代表它们能够解释更多的数据变异性。
基本概念
- 方差(Variance): 方差是用来衡量随机变量离其期望值的距离的度量。对于一个向量或者一组数据,其方差表示数据在各个维度上的离散程度。方差越大,表示数据在该维度上的变化范围越广。公式如下:
其中,表示第
个数据点,
表示数据的平均值,
表示数据点的总数。
-
协方差(Covariance):用于描述两个随机变量之间的线性关系。对于两个随机变量X和Y,可以使用以下公式计算它们的协方差:
其中,和
分别表示第
个数据点的
和
的取值,
和
分别表示
和
的平均值,
表示数据点的总数。
-
协方差矩阵(Covariance Matrix):描述数据集中各个维度之间协方差的矩阵形式。假设有一个n维数据集,其中每个数据点包含m个维度的取值,可以使用以下公式计算协方差矩阵:
其中,A表示将数据中心点移至原点的矩阵的矩阵,T表示矩阵的转置。
PCA算法描述:

即将协方差的d个特征向量作为基底,再将原数据投影再新基底上
代码展示
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Ddef PCA(data, k):data = data - np.mean(data, axis=0) # 将中心点移到原点cov_matrix = np.cov(data, rowvar=False) # 计算协方差矩阵# rowvar=False:这表示每一列代表一个特征,每一行代表一个样本。# 如果设为True,则表示每一行代表一个特征,每一列代表一个样本。eigvalues, eigvactors = np.linalg.eig(cov_matrix) # 计算特征值和特征向量# 选特征值最大的k给特征向量作为基底new_base = eigvactors[:,np.argsort(-eigvalues)[:k]]transformed_data = np.dot(data, new_base) # 降维return transformed_data生成数据,降维展示
# 生成三维数据
data = np.random.rand(200, 3)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[:, 0], data[:, 1], data[:, 2])
plt.show()
# 使用 PCA 将数据降维到 2 维
transformed_data = PCA(data, 2)
# 画出降维后的数据点
plt.scatter(transformed_data[:, 0], transformed_data[:, 1])
plt.show()展示:
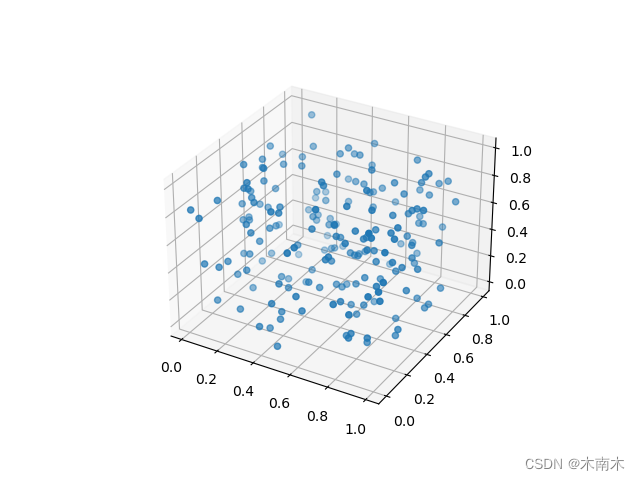
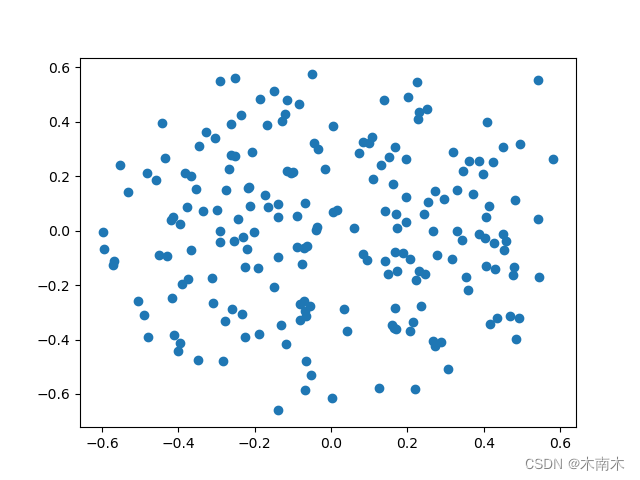
这篇关于《三体》二向箔的降维打击——PCA算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







