【LetMeFly】889.根据前序和后序遍历构造二叉树：分治（递归）——双O(n)的做法，五彩斑斓的题解（若不是彩色的可以点击原文链接查看）

本文主要是介绍【LetMeFly】889.根据前序和后序遍历构造二叉树：分治（递归）——双O(n)的做法，五彩斑斓的题解（若不是彩色的可以点击原文链接查看），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【LetMeFly】889.根据前序和后序遍历构造二叉树：分治（递归）——双O(n)的做法，五彩斑斓的题解（若不是彩色的可以点击原文链接查看）

力扣题目链接：https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-postorder-traversal/

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中任何一个。

示例 1：

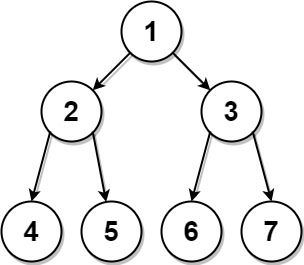
输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

示例 2:

输入: preorder = [1], postorder = [1]
输出: [1]

提示：

1 <= preorder.length <= 30
1 <= preorder[i] <= preorder.length
preorder 中所有值都不同
postorder.length == preorder.length
1 <= postorder[i] <= postorder.length
postorder 中所有值都不同
保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

方法一：分治（递归）——双O(n)的做法

做这道题前强烈建议先去做一下从前序与中序建树。我们知道：

前序遍历：根左子树右子树
后序遍历：左子树右子树根

我们需要明白：左子树和右子树只有一个的情况下，仅仅通过前序遍历和后续遍历的结果是无法得到原树是左子还是右子的。这是因为，对于某个只有一个子树的节点：

假设此节点只有左子树，那么遍历结果为：前序【根左子树】后序【左子树根】
假设此节点只有右子树，那么遍历结果为：前序【根右子树】后序【右子树根】

仅凭遍历结果无法得知到底是左子树还是右子树

因此我们可以按照“只有一个子树的情况下将其还原为左子树”的方式进行建树。

因此我们可以写一个函数dfs接收前序遍历数组和后序遍历数组作为参数：

以前序遍历数组的第一个节点（或者说后序遍历数组的最后一个节点）为根

如果前序遍历数组的长度为1，那么说明只有根节点，直接返回。

否则必定存在左子树（前面我们得出了结论，即使只有一个子树也可以视为左子树）。因此我们只需要得到左子树和右子树（可能为空但无所谓）的长度，就能在前序遍历数组和后序遍历数组中将二者划分出来，并继续递归。确定左子树长度的方法为：

在前序遍历数组中，左子树的第一个节点为左子树的根节点。

在后序遍历数组中，左子树的最后一个节点为左子树的根节点。

因此从前序遍历数组中可以得到左子树的根节点，由这个节点在后序遍历数组中的位置，能得到左子树的长度。

从而右子树的长度也能从任意一个遍历数组中，减去左子树的长度（减根节点的长度）得出。

递归的终止条件为“前序遍历数组为空”，此时返回空节点。

Tips: 可以在预处理时建立一个哈希表，以便能快速地找到左子树的根节点在后序遍历数组中的位置。

时间复杂度 $O (N)$ ，其中 $N$ 是节点个数
空间复杂度 $O (N)$

AC代码

C++

class Solution {
private:unordered_map<int, vector<int>::iterator> ma;TreeNode* dfs(vector<int>::iterator preLeft, vector<int>::iterator preRight, vector<int>::iterator postLeft, vector<int>::iterator postRight) {if (preLeft >= preRight) {return nullptr;}if (preLeft + 1 == preRight) {  // 只有一个节点return new TreeNode(*preLeft);}int leftLength = leftLength = ma[*(preLeft + 1)] - postLeft + 1;  // 注意是*(preLeft + 1)return new TreeNode(*preLeft,dfs(preLeft + 1, preLeft + 1 + leftLength, postLeft, postLeft + leftLength),dfs(preLeft + 1 + leftLength, preRight, postLeft + leftLength, postRight - 1));}
public:TreeNode* constructFromPrePost(vector<int>& preOrder, vector<int>& postOrder) {for (vector<int>::iterator it = postOrder.begin(); it != postOrder.end(); it++) {ma[*it] = it;}return dfs(preOrder.begin(), preOrder.end(), postOrder.begin(), postOrder.end());}
};

Python

# from typing import List, Optional# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = rightclass Solution:def dfs(self, preOrder: List[int], preLeft: int, preRight: int, postOrder: List[int], postLeft: int, postRight: int) -> Optional[TreeNode]:if preLeft >= preRight:return Noneif preLeft + 1 == preRight:return TreeNode(preOrder[preLeft])leftLength = self.ma[preOrder[preLeft + 1]] - postLeft + 1return TreeNode(preOrder[preLeft],self.dfs(preOrder, preLeft + 1, preLeft + 1 + leftLength, postOrder, postLeft, postLeft + leftLength),self.dfs(preOrder, preLeft + 1 + leftLength, preRight, postOrder, postLeft + leftLength, postRight - 1))def constructFromPrePost(self, preOrder: List[int], postOrder: List[int]) -> TreeNode:self.ma = dict()for i in range(len(postOrder)):self.ma[postOrder[i]] = ireturn self.dfs(preOrder, 0, len(preOrder), postOrder, 0, len(postOrder))