作者:桂。
时间:2017-03-26 06:06:44
链接:http://www.cnblogs.com/xingshansi/p/6621185.html
声明:欢迎被转载,不过记得注明出处哦~

【读书笔记04】
前言
仍然是西蒙.赫金的《自适应滤波器原理》第四版第二章,首先看到无约束维纳滤波,接着到了一般约束条件的滤波,此处为约束扩展的维纳滤波,全文包括:
1)背景介绍;
2)广义旁瓣相消(Generalized Sidelobe Cancellation, GSC)理论推导;
3)GSC应用——语音阵列信号增强;
内容为自己的学习记录,其中错误之处,还请各位帮忙指正!
一、背景介绍
在一般约束条件的维纳滤波中,有${{\bf{w}}^H}{\bf{s}}\left( {{\theta _0}} \right) = g$的约束条件,即${{\bf{s}}^H}\left( {{\theta _0}} \right){\bf{w}} = g$.如${\bf{s}}\left( {{\theta _0}} \right)$为旋转向量时,希望在$\theta _0$处保留波束—>对应$g_1 = 1$,希望在$\theta_2$处抑制波束—>对应$g_2 = 0$,写成一般形式:
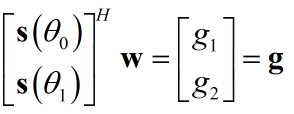
写成更一般的形式:
${{\bf{C}}^H}{\bf{w}} = {\bf{g}}$
假设$\bf{w}$权值个数为M,在一般约束维纳滤波中可以看出:限定条件使得结果更符合预期的效果。假设C为M×L的矩阵:L个线性约束条件。对于M个变量的方程组,对应唯一解最多有M个方程,即:对于L个线性约束来讲,我们仍可以继续利用剩下的M-L个自由度进行约束,使得结果更加符合需求(比如增强某信号、抑制某信号等),这便是GSC的背景。
二、GSC理论推导
A-理论介绍
书中的推导较为繁琐,我们可以从投影空间的角度加以理解,也就是最小二乘结果的矩阵求逆形式,给出简要说明:
对于矩阵A(N×M):
- 如果A是满列秩(N>=M)对于符合LA=I的矩阵解为:${\bf{L}} = {\left( {{{\bf{A}}^H}{\bf{A}}} \right)^{ - 1}}{{\bf{A}}^H}$;
- 如果A是满行秩(N<=M)对于符合AR=I的矩阵解为:${\bf{R}} = {{\bf{A}}^H}{\left( {{{\bf{A}}}{\bf{A}^H}} \right)^{ - 1}}$.
对于${{\bf{C}}^H}{\bf{w}} = {\bf{g}}$,得出最优解:
${{\bf{w}}_q} = {\bf{C}}{\left( {{{\bf{C}}^H}{\bf{C}}} \right)^{ - 1}}{\bf{g}}$
记:
${{\bf{w}}_{re}} = {\bf{w}} - {{\bf{w}}_q}$
为了便于对余量${{\bf{w}}_{re}}$进行控制,将C扩展为:[ C | C$_{a}$ ],$\bf{C}_a$的列向量为矩阵C列向量张成空间的正交补空间的基,即:
${\bf{C}}_a^H{\bf{C}} = {\bf{0}}$
分析新的空间特性:
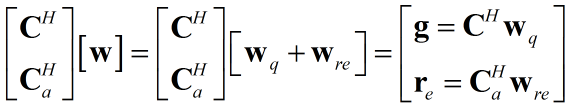
上式有${{\bf{C}}^H}{{\bf{w}}_{re}} = {\bf{0}}$,这就说明只要满足该条件,${{\bf{r}}_e} = {\bf{C}}_a^H{{\bf{w}}_{re}}$就是补空间的余量,如何保证一定有${{\bf{C}}^H}{{\bf{w}}_{re}} = {\bf{0}}$呢?可以将${{{\bf{w}}_{re}}}$写为:${ - {{\bf{C}}_a}{{\bf{w}}_a}}$的形式,之所以添加$-$可能是因为正交补空间可以认为C列向量空间不能表征的成分,我们通常认为这一部分为该丢弃的残差,也因为是残差:${{\bf{C}}_a}$通常被称为阻塞矩阵(取Block之意),很多书籍用$\bf{B}$表示。
重新给出推导的结果:
${\bf{w}} = {{\bf{w}}_q} - {{\bf{C}}_a}{{\bf{w}}_a}$ s.t. ${{\bf{C}}_a}{{\bf{w}}_q} = {\bf{0}}$
对应结构图为:
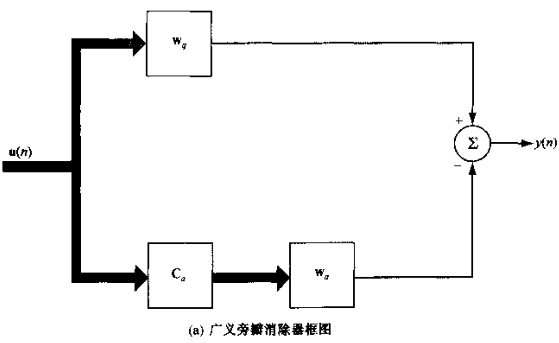
简化后可以认为上支、下支:
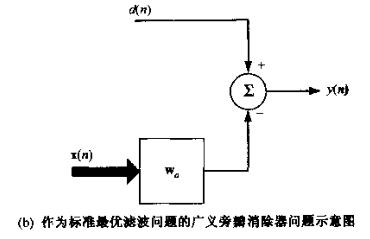
这是维纳滤波器的典型结构。
B-阻塞矩阵的选取
阻塞矩阵这一段摘自:秦博雅《基于低复杂度自适应信号处理的波束成形技术研究》p22~23.
大致有以下几种方式:
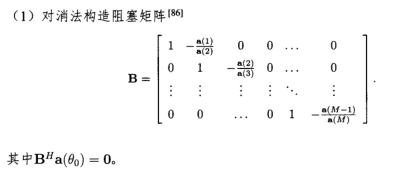



三、阵列信号增强
学了这个GSC怎么应用呢?这里参考一篇07年adaptive beamforming(引用见最后的参考)的例子,简要说明思路,关于阻塞矩阵。
文中结构图:
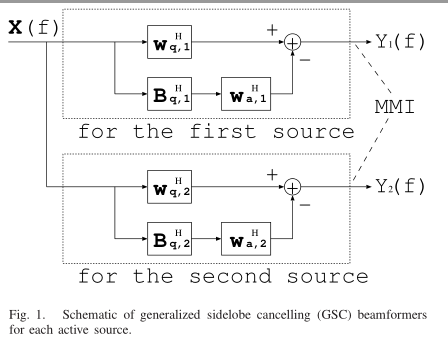
即:分别利用GSC框架,通过最小互信息实现信号的分离,其中$w_a$、$C_a$即$B$都提前给定,优化$w_{a1}$、$w_{a2}$。
定义互信息:

其中,
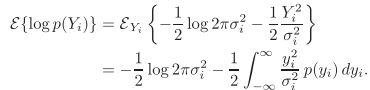

在幅度(严格来讲是傅里叶系数幅度)为正态条件下,得到:
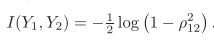
给出输出表达式:
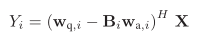
并给出准则函数——相关系数的表达式:
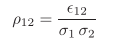
其中,
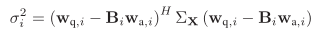
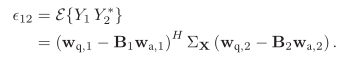
其中相关、互相关无法得到统计信息,仍然可以基于遍历性假设:利用时间换取空间,近似求取。
文中提到引入正则化(regularization)

这个只是优化过程中的限定条件,与GSC框架关系不大,不再补充。
这里在网上找去了一个8通道(channel)的混合语音(两个说话人),利用该算法进行分析,给出主要代码:
主要代码:
MMI_define_var(Xf1,Xf2); %initialization W1 = [0 0 0 0.1 0 0 0.2 ]; W2 = [0 2 0 0 0.2 0 0.1 ]; [Wa1,Wa2]=MMI_EstimateWa([W1 W2]');
其中MMI_define_var定义变量:
function MMI_define_var(Xf1,Xf2)global Wq B covX1X1 covX2X2 covX1X2 len;Wq=[1 1 1 1 1 1 1 1]'*1/8; B=[1 -1 0 0 0 0 0 0 ;0 1 -1 0 0 0 0 0 ;0 0 1 -1 0 0 0 0 ;0 0 0 1 -1 0 0 0 ;0 0 0 0 1 -1 0 0 ;0 0 0 0 0 1 -1 0 ;0 0 0 0 0 0 1 -1 ]';[~,len]=size(Xf2); XfMean1=mean(Xf1.'); XfMean2=mean(Xf2.'); for i=1:8Xf1(i,:)=Xf1(i,:)-XfMean1(i);Xf2(i,:)=Xf2(i,:)-XfMean2(i); endcovX1X1=Xf1*Xf1'/len; covX2X2=Xf2*Xf2'/len; covX1X2=Xf1*Xf2'/len;
MMI_EstimateWa实现参数估计:
function [Wa1 Wa2]=MMI_EstimateWa(W)
%obtain the Wa
ww=[real(W)' imag(W)']';options = optimset('LargeScale','off','display','off');
[X,fval] = fminunc('MMI_real_imag_objfun',ww,options);
X_real=X(1:14);
X_imag=X(15:28);
Wa1_real=X_real(1:7);
Wa1_imag=X_imag(1:7);
Wa2_real=X_real(8:14);
Wa2_imag=X_imag(8:14);Wa1=Wa1_real+sqrt(-1)*Wa1_imag;
Wa2=Wa2_real+sqrt(-1)*Wa2_imag;
end
对应结果图:

可以听出来:虽然略有杂音,但两个说话人的声音已经实现了分离,GSC框架有效。如果不同说话人声达时间估计准确,迭代算法应用合适,效果会更好,此处主要介绍GSC应用,细节不再琢磨,有兴趣的可以探索探索。
参考:
- K. Kumatani, T. Gehrig, U. Mayer, E. Stoimenov, J. McDonough and M. WÖlfel, "Adaptive Beamforming With a Minimum Mutual Information Criterion," in IEEE Transactions on Audio, Speech, and Language Processing, vol. 15, no. 8, pp. 2527-2541, Nov. 2007.
- Simon Haykin 《Adaptive Filter Theory Fourth Edition》.







