图的最短路径之(迪克斯特拉）Dijkstra算法代码实现

本文主要是介绍图的最短路径之(迪克斯特拉）Dijkstra算法代码实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一，Dijkstra算法

１，初始化：先找出从源Ｖ0到各终点Vk的直达路径（Ｖ0,Vk),即通过一条弧到达的路径．如果一条弧不能到达的点记为　无穷大

２，选择：从这些路径中找出一条长度最短的路径（V0,U).

3，更新：然后从其余各条路径进行适当调整：

若在图中存在弧（U,Vk),且(V0,U) + (U,Vk) < (V0,Vk),则以路径(V0,U,Vk)代替(V0,Vk)

4，在调整后的各条路径中，再找长度最短的路径（依此类推）．

具体的操作为：

１，把Ｖ（顶点）分成两组：

（１）Ｓ：已求出最短路径的顶点集合．

（２）Ｔ　＝　Ｖ - S：尚未确定最短路径的顶点集合．

２，将Ｔ中顶点按最短路径递增的次序加入到Ｓ中．

要保证：（１）从源点Ｖ0到Ｓ中条顶点的最短路径长度都不大于从Ｖ0到Ｔ中任何顶点

　　　　　　　的最短路径长度．

（２）每个顶点对应一个距离值：

Ｓ中顶点：从Ｖ.到此顶点的最短路径长度

Ｔ中顶点：从Ｖ0到此顶点的只包括Ｓ中顶点作中间顶点的最短路径长度．

举个例子：

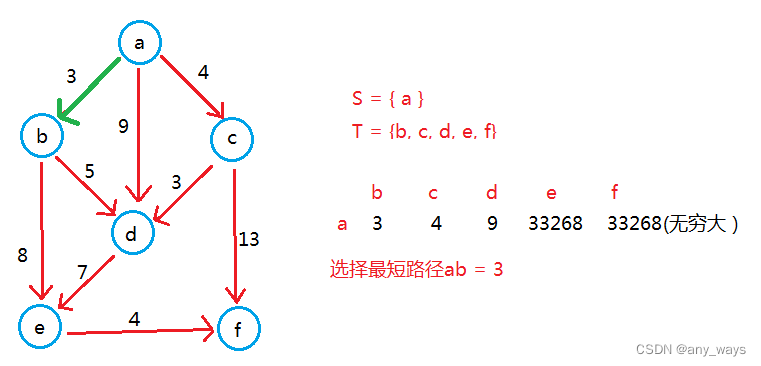
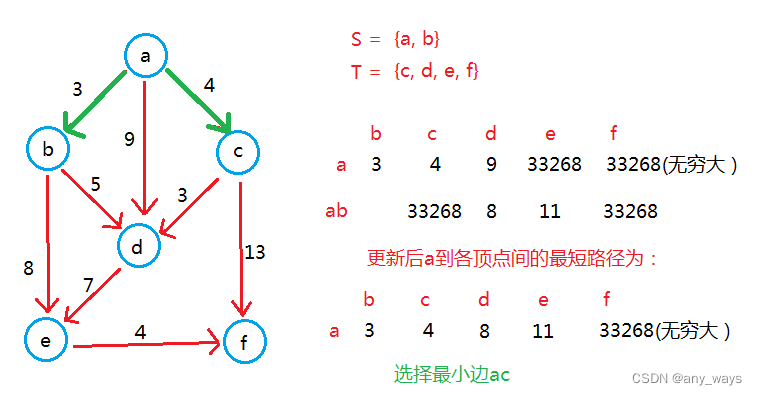
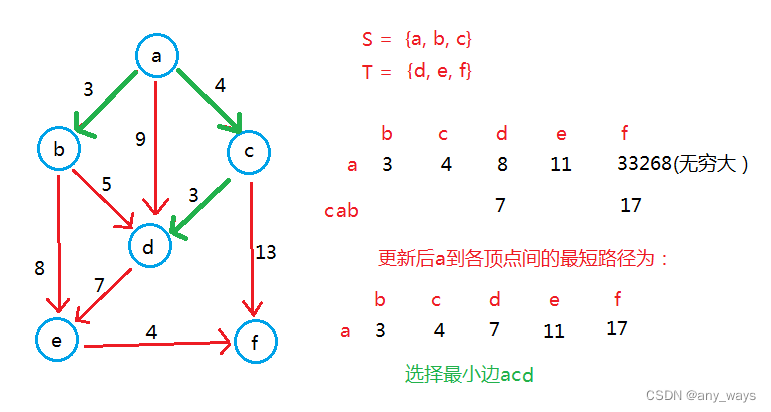
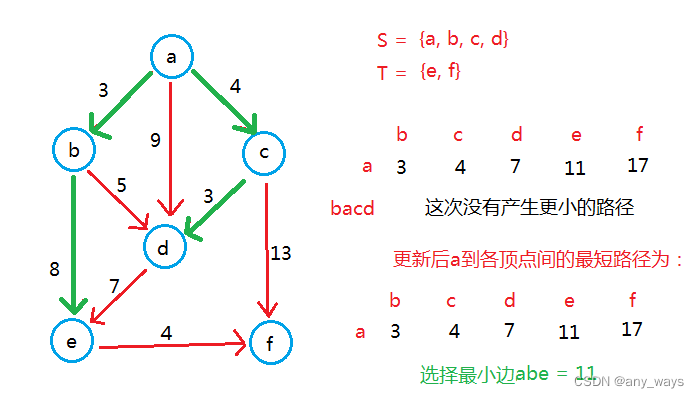
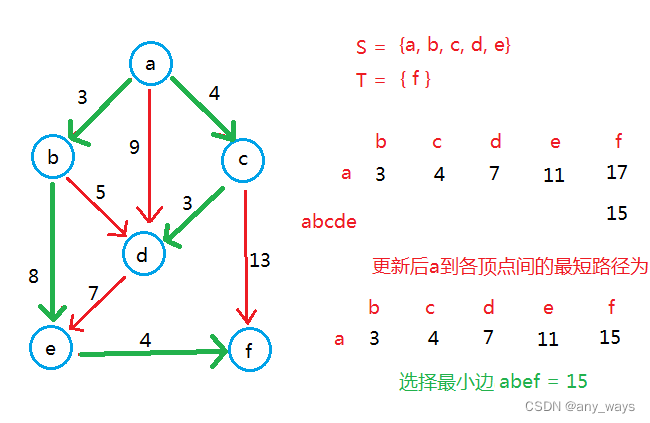
最终：Ｓ = {a, b, c, d, e, f},T={}.

a到各顶点间的最短路径为：ab = 3, ac = 4, ad = 7, ae = 11, af = 15.

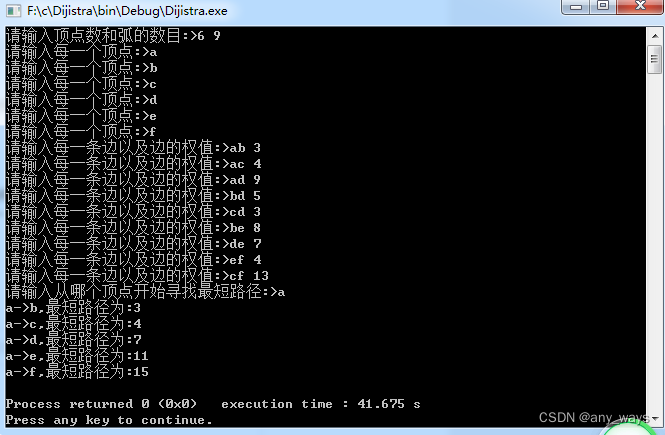
二，以上面的例子，代码的实现

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
#define MAXINT 10000
typedef struct{//表示顶点，包含名称和权重char data;int weight;
}vertex;typedef struct{//表示顶点集合，包含顶点数组和顶点个数vertex arr[MAXSIZE];int size;
}VertexSet;
int get_index(VertexSet a, char b)//根据输入顶点的名称，得到该顶点在数组中的下标
{int i = 0;for(i = 0; i < a.size; i++){if(a.arr[i].data == b)return i;}return -1;
}void Dijkstra(VertexSet* S, VertexSet T, int G[MAXSIZE][MAXSIZE])
{int m,n,i,j;for(i = 0; i < MAXSIZE; i++){for(j = 0; j < MAXSIZE; j++){G[i][j] = MAXINT;//初始化邻结矩阵}}T.size = 0;S->size = 0;int visited[MAXSIZE] = {0};printf("请输入顶点数和弧的数目:>");scanf("%d%d",&m,&n);for(i = 0; i < m; i++){printf("请输入每一个顶点:>");getchar();scanf("%c",&T.arr[i].data);T.arr[i].weight = MAXINT;//初始化Ｔ集合，权值为极大，以及顶点个数T.size++;}char a,b;int q;for(i = 0; i < n; i++){printf("请输入每一条边以及边的权值:>");getchar();scanf("%c%c%d",&a,&b,&q);G[get_index(T,a)][get_index(T,b)] = q;//保存输入的边以及权值到二维数组Ｇ}char input;printf("请输入从哪个顶点开始寻找最短路径:>");getchar();scanf("%c",&input);S->arr[0].data = input;//Ｓ集合中放入第一个值，就是你输入的开始顶点S->arr[0].weight = 0;//设置权值为0S->size++;//Ｓ集合中元素个数+１visited[get_index(T, input)] = 1;//标记该顶点为已访问int temp_index = get_index(T,input);//得到出发点的下标，相当于二维数组的横坐标while(S->size < T.size ){int temp_min = MAXINT;for(i = 0;i < T.size; i++){//更新Ｔ集合中，通过Ｓ集合中顶点中转，到各顶点间的最短路径if(T.arr[i].weight >= G[temp_index][i]+S->arr[S->size-1].weight && !visited[i]){T.arr[i].weight = G[temp_index][i]+S->arr[S->size-1].weight;}if(!visited[i] && temp_min >= T.arr[i].weight){temp_min = T.arr[i].weight;//找到更新后的Ｔ集合中，最小的权值，以及它在数组中的下标j = i;//下标}}temp_index = j;//找到最短路径顶点后，下次循环就以这个顶点为中转，到其它各顶点间的路径visited[temp_index] = 1;//循环一次Ｓ集合添加一个元素，Ｓ集合元素个数+１S->arr[S->size].weight = temp_min;S->arr[S->size].data = T.arr[temp_index].data;S->size++;}
}
void Print(VertexSet S)
{int i;for(i = 1; i < S.size; i++){printf("%c->%c,最短路径为:%d\n",S.arr[0].data,S.arr[i].data,S.arr[i].weight);}
}int main()
{int G[MAXSIZE][MAXSIZE];//用邻结矩阵来表示有向网VertexSet T,S;//Ｓ集合表示从指定顶点出发，到各顶点的最短路径的集合，Ｔ集合表示当前指定顶点到各顶点间的路径集合Dijkstra(&S,T,G);Print(S);return 0;
}