本文主要是介绍Peter算法小课堂—背包问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们已经学过好久好久的动态规划了,动态规划_Peter Pan was right的博客-CSDN博客
那么,我用一张图片来概括一下背包问题。

大家有可能比较疑惑,优化决策怎么优化呢?答案是,滚动数组,一个神秘而简单的东西。
01背包
题目:小偷来你家,他带的包只能装c斤的财务。你家有n种财务,分别重w1、w2......wn斤,价值分别为v1、v2......,请输出能拿走的最大总价值?
大家思考一下状态定义和状态转移方程。
额……
状态定义
f[i][j]:用前i个物品,每个物品只能选或不选,满足重量和小于等于j的所有选法中,价值最高的那个方案。最终答案:f[n][c]
状态转移方程
首先,我们分两种情况讨论:1.选i 2.不选i
1。 此时我们重量和会变小w[i],但是价值会增加v[i],f[i][j]=f[i-1][j-w[i]]+v[i]
2。 此时物品数减1,f[i][j]=f[i-1][j]
最后,再取最大值,得到状态转移方程:f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i])
代码①
for(int i=1;i<=n;i++) cin>>w[i]>>v[i];
for(int i=1;i<=n;++i){for(int j=1;j<=c;++j){if(w[i]>j) f[i][j]=f[i-1][j];else f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);}
}
cout<<f[n][c]<<endl;有点费空间,要开滚动数组
代码②
滚动数组,给大家看个图

我们发现,dp[i][j]这一格,只需要i-1这一行,i-2、i-3……都不需要。题目如果并没有要求中间的状态(比如输出背包的方案),我们就可以将其省略来节省空间的使用。所以我们可以只用一维数组dp[j]来记录数据dp[i][j]的状态,在更新的过程中不断用新的数据dp[j] (dp[i][j]) 覆盖掉旧的数据dp[j](dp[i-1][j])。大家听懂了吗???
代码呢?
#include <bits/stdc++.h>
using namespace std;
const int MAXC=2009;
int n,c,w,v,f[MAXC];
int main(){cin>>c>>n;for(int i=1;i<=n;i++){cin>>w>>v;for(int j=c;j>=w;j--)f[j]=max(f[j],f[j-w]+v);}cout<<f[c]<<endl;return 0;
}大家可能会疑惑,为什么第二层循环要倒着推啊,我给出一个解释。我们每次计算dp[j] (即dp[i][j]) 的时候都会需要dp[j-w[i]] (即dp[i-1][j-w[i]])的值。所以如果我们正序计算,那么dp[j-w[i]]就已经更新了 (即用过之前的背包了),与每个背包只能用1次不符。那么,这不就是完全背包要的吗?
完全背包
题目:小偷来你家,他带的包只能装c斤的财务。你家有n种财务,每种数量无限多,分别重w1、w2......wn斤,价值分别为v1、v2......,请输出能拿走的最大总价值?
题解请看01背包,这里只给出代码
cin>>c>>n;
for(int i=1;i<=n;i++){cin>>w>>v;for(int j=w;j<=c;j++)f[j]=max(f[j],f[j-w]+v);
}
cout<<f[c]<<endl;分组背包


分组01与普通01的区别就是,分组01有两组策略:1.选择本组的某一件 2.一件不选

所以说,分组背包编码很麻烦
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll G=19;
const ll N=39;
const ll MAXV=209;
ll c,n,g,f[MAXV];
vector<ll> w[G],v[G];
int main(){cin>>c>>n>>g;for(ll i=1;i<=n;i++){ll ww,vv,p;cin>>ww>>vv>>p;w[p].push_back(ww);v[p].push_back(vv);}for(ll i=0;i<=g;i++){//枚举组号for(ll j=c;j>=0;j--){//枚举载重for(ll k=0;k<w[i].size();k++){//枚举物品if(j>=w[i][k]) f[j]=max(f[j],f[j-w[i][k]]+v[i][k]);}}}cout<<f[c]<<endl;return 0;
}多重背包

多重背包怎么办呢,这里,我们要采用二进制拆分。

就是……这样
void bb01(int w,int v){for(int j=c;j>=w;j--)f[j]=max(f[j],f[j-w]+v);
}
int main(){cin>>n>>c;for(int i=1;i<=n;i++){cin>>w>>v>>s;for(int k=1;k<=s;s-=k;k*=2) bb01(k*w,k*v);if(s) bb01(s*w,s*v);}cout<<f[c]<<endl;return 0;
}简单吧,其实为什么这里我都没有进行仔细的讲解,是因为……不会,再多思考思考01背包和图片。
混合背包
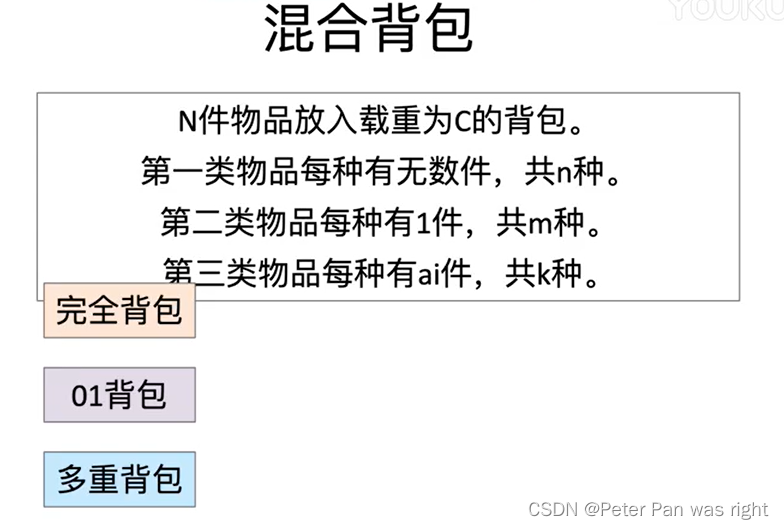
大家试着写写。大家有兴趣的话可以去往上搜搜“背包九讲”。
希望这些对大家有用,三连必回
这篇关于Peter算法小课堂—背包问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






