【晴问算法】入门篇—贪心算法—经典例题和个人题解

OJ平台链接：https://sunnywhy.com/sfbj/4/4/149

什么是贪心算法？

贪心算法的定义：采用局部最优的策略能得到全局最优的结果，即贪心选择性质。
除了贪心选择性质以外，能用贪心算法解决的问题还必须具有最优子结构性质。
最优子结构性质：问题的最优解所包含的子问题的解也是最优的
然而，并不是所有问题都适用贪心算法，完全适用贪心算法的问题必须具有最优子结构性质和贪心选择性质。针对不完全适用的问题，利用贪心算法，往往只能得到较优解，而并非是最优解。
通俗地讲，假如贪心算法适用于统一天下的问题，那么，刘皇叔完全不用考虑天下大势，每次只要让当前战役所取得的利益最大，损失最小，他就能统一天下。
贪心选择性质意味着只要局部利益最大化就一定能达到全局利益最大化，追求当前局部利益最大化不会损失往后的局部利益，不存在着为了长远利益，而主动牺牲当前的利益这样的现象，只需考虑眼前的利益最大化就可以了，就一定能够达成全局利益最大化的结果。

1. 最优装箱

题目描述
有$n$个箱子需要装上一艘轮船，已知第$i$个箱子的重量为$w_i$，轮船的载重为$W$。问在不超过轮船载重的前提下，最多能把多少个箱子装上轮船。

输入描述
第一行两个正整数$n$、$W$（$1\le n\le 10^5$、$1\le W\le 10^7$），分别表示箱子个数和轮船载重。

第二行$n$个正整数$w_i$（$1\le w_i\le 10^7$），表示$n$个箱子的重量。

输出描述
输出两个整数，分别表示能装上轮船的箱子个数和总重量，用空格隔开。

样例1
输入
5 11
7 2 9 1 11
输出
3 10
解释
能将重量分别为7、2、1的箱子装上轮船（此时箱子个数最多），总重量为10。

下面是对这道题的解答：

贪心策略： 对箱子按照重量从小到大排序，每次拿箱子都拿重量最小的那个箱子，直到不能拿为止（不允许总重量超过轮船载重）。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<map>
#include<set>
using namespace std;int a[100005]; //表示每个箱子的重量
int main(){int i,n,W;int sum = 0; //sum表示当前已拿箱子的总重量int cnt = 0; //cnt表示当前已拿箱子的数量scanf("%d%d",&n,&W); //n表示箱子个数，W表示轮船最大载重for(i=0;i<n;i++){scanf("%d",&a[i]); //读入每个箱子的重量}sort(a,a+n); //按箱子的重量从小到大排序，贪心策略是优先选择重量小的箱子for(i=0;i<n;i++){if(sum+a[i]>W) break; //如果拿了当前的箱子会导致超重的话，就不再继续拿箱子else{//如果不会超重，那么拿当前的箱子cnt++; //已拿箱子个数加1sum+=a[i];//已拿箱子的总重量加上新拿箱子的重量}}printf("%d %d\n",cnt,sum);return 0;
}

2. 整数配对

题目描述
有两个正整数集合$S$、$T$，其中$S$中有$n$个正整数，$T$中有$m$个正整数。定义一次配对操作为：从两个集合中各取出一个数$a$和$b$，满足$a\in S$、$b\in T$、$a\le b$，配对的数不能再放回集合。问最多可以进行多少次这样的配对操作。

输入描述
第一行两个正整数$n$、$m$（$1\le n\le 10^4$、$1\le m\le 10^4$），分别表示$S$和$T$中正整数的个数。

第二行$n$个正整数（$1\le a_i\le 10^5$），表示$S$中的$n$个正整数。

第三行$m$个正整数（$1\le b_i\le 10^5$），表示$T$中的$m$个正整数。

输出描述
输出一个整数，表示最多的配对操作次数。

样例1
输入
3 3
2 5 3
3 3 4
输出
2
解释
2与其中一个3配对，3与另一个3配对，5无法和4配对。因此最多配对两次。

下面是对这道题的解答：

贪心策略： 对集合S和集合T均从小到大排序，针对集合S中的每一个元素，选择集合T中尽可能小的但是又比集合S中的当前元素大的元素，保证配对总数最大，避免非常小的元素配对非常大的元素，导致其它元素配不到对。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<map>
#include<set>
using namespace std;int main(){int n,m,tp,i,j;int sum = 0;//表示当前已配对数vector<int> v1,v2; //向量v1存储集合S的元素，向量v2存储集合T的元素scanf("%d%d",&n,&m);for(i=0;i<n;i++){scanf("%d",&tp); //读入集合S的元素，允许重复v1.push_back(tp); //将元素放入集合S}sort(v1.begin(),v1.end()); //对集合S的元素从小到大排序for(i=0;i<m;i++){scanf("%d",&tp); //读入集合T的元素，允许重复v2.push_back(tp); //将元素放入集合T}sort(v2.begin(),v2.end()); //对集合T的元素从小到大排序j = 0;for(i=0;i<n;){if(v1[i]<=v2[j]){ //如果集合S当前元素小于等于集合T当前元素，可以配对sum++; //配对数加1i++; //配对成功，开始对集合S的下一个元素寻找配对元素}j++; //考虑集合T的下一个元素if(j==m) break; //如果已经到达集合T的最后一个元素，意味着集合T不再有可以配对的元素}printf("%d\n",sum);return 0;
}

3. 最大组合整数

题目描述
现有0~9中各个数的个数，将它们组合成一个整数，求能组合出的最大整数。

输入描述
在一行中依次给出0-9中各个数的个数（所有个数均在0-100之间）。数据保证至少有一个数的个数大于0。

输出描述
输出一个整数，表示能组合出的最大整数。

样例1
输入
1 0 2 0 0 0 0 0 0 1
输出
9220
解释
存在1个0、2个2、1个9，因此能组合出的最大整数是9220

下面是对这道题的解答：

贪心策略： 要想使得输出整数最大，只要让每次输出的数都是当前可用的最大数，例如，先输出9，再输出8，再7，以此类推，最后输出0，始终让当前可用的最大的数字位于整数的高位，这能保证整数最大。如果某个数字有多个可用，那就输出多个，如果某个数字只有0个可用，那就不用，将其跳过。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<map>
#include<set>
using namespace std;int main(){int a[10]; //存储0-9当中每个数的出现次数int i;int flag = false; //是否是第一个输出的数字for(i=0;i<10;i++){scanf("%d",&a[i]);}for(i=9;i>=0;i--){  //从大到小输出数字，最先输出9，最后输出0，这能保证组合而成的整数最大if(a[i]>0){if(!flag&&i==0){ //如果第一个输出的数字是0，意味着只有0可以用printf("0"); //只输出一个0break;}while(a[i]!=0){ //将当前数字的次数全部用完printf("%d",i); //输出当前数字a[i]--; //可用个数减一}flag = true; //表示已经输出了第一个数字}}printf("\n");return 0;
}

4. 区间不相交问题

题目描述
给定个开区间，从中选择尽可能多的开区间，使得这些开区间两两没有交集。

输入描述
第一行为一个正整数$n$（$1\le n\le 10^4$），表示开区间的个数。

接下来$n$行，每行两个正整数$x_i$、$y_i$（$0\le x_i\le 10^5$、$0\le y_i\le 10^5$），分别表示第$i$个开区间的左端点和右端点。

输出描述
输出一个整数，表示最多选择的开区间个数。

样例1
输入
4
1 3
2 4
3 5
6 7
输出
3
解释
最多选择(1,3)、(3,5)、(6,7)三个区间，它们互相没有交集。

下面是对这道题的解答：

贪心策略： 如果要使选取的区间没有交集，必须保证一个区间的左端点比另一个区间的右端点大，而且两两之间如此。所以，优先选取右端点小的而且左端点比上一个选取的区间的右端点大的那个区间，既保证没有交集，又保证右端点较小，为选取更多区间提供了机会。
实际上，在不交叉的前提下，优先选取的是区间长度短并且最靠左的区间，不容易挤占其它区间的空间，如此可选的区间会最多。

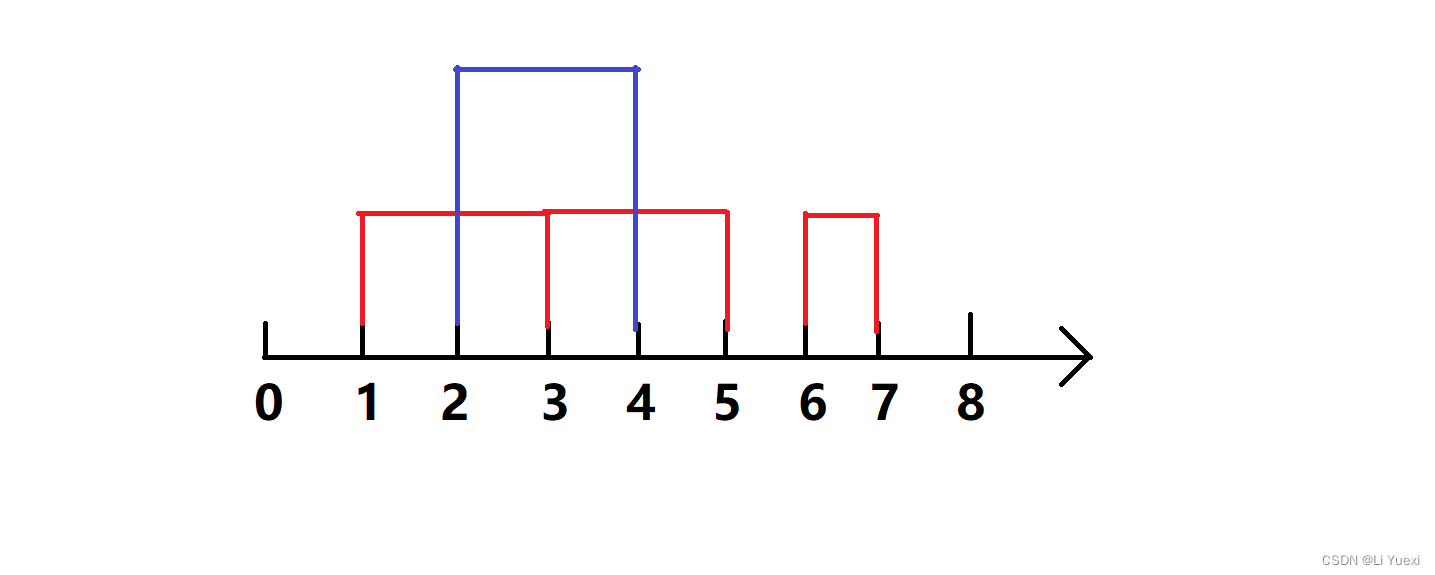
如上图所示，红色为选取的区间，蓝色为不选的区间。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<map>
#include<set>
using namespace std;struct qujian{int x,y; //x为区间左端点，y为区间右端点
};bool cmp(qujian a,qujian b){ //比较函数，y值小的排在y值大的前面return a.y<b.y;
}
qujian q[10005];
int main(){int i,n;int sum = 1; //当前已选择的开区间个数int last; //上一个选取的区间的右端点值scanf("%d",&n);//n表示区间个数for(i=0;i<n;i++){scanf("%d%d",&q[i].x,&q[i].y); //读入每个区间的区间左端点和区间右端点}	sort(q,q+n,cmp); //对每个区间按照区间右端点从小到大排序，优先选右端点小的区间last = q[0].y; //区间右端点最小的区间一定可以选取for(i=1;i<n;i++){if(q[i].x>=last){ //如果当前区间的左端点比上一个选取的右端点还要大，则可以选取，一定没有交集sum++;//选取开区间数加1last = q[i].y; //存储该区间的右端点，以供下一个选取的区间的左端点和其比较}}printf("%d\n",sum);return 0;
}

5. 区间选点问题

题目描述
给定$n$个闭区间，问最少需要确定多少个点，才能使每个闭区间中都至少存在一个点。

输入描述
第一行为一个正整数$n$（$1\le n\le 10^4$），表示闭区间的个数。

接下来$n$行，每行两个正整数$x_i$、$y_i$（$0\le x_i\le 10^5$、$0\le y_i\le 10^5$），分别表示第$i$个闭区间的左端点和右端点。

输出描述
输出一个整数，表示最少需要确定的点的个数。

样例1
输入
3
1 4
2 6
5 7
输出
2
解释
至少需要两个点（例如3和5）才能保证每个闭区间内都有至少一个点。

下面是对这道题的解答：

贪心策略： 对每个区间按照右端点从小到大排序，尽量选取区间的右端点作为确定点，该点能和最多的区间重合。

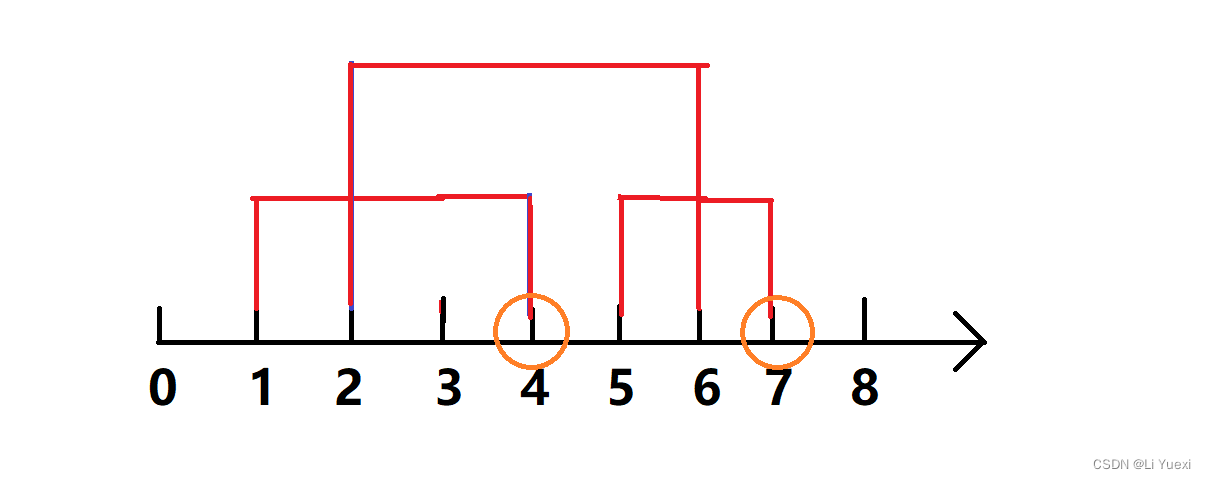
如上图所示，圆圈指的是确定点。
代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<map>
#include<set>
using namespace std;struct qujian{int x,y;
};bool cmp(qujian a,qujian b){ //比较函数if(a.y!=b.y) return a.y<b.y;else return a.x<b.x;
}
qujian q[10005];
int main(){int n,i;int sum = 1; //sum表示确定的点数scanf("%d",&n);for(i=0;i<n;i++){scanf("%d%d",&q[i].x,&q[i].y);//读入每个区间的左端点和右端点}sort(q,q+n,cmp); //对区间按照右端点从小到大排序int last = q[0].y; //将第一个区间的右端点作为确定点for(i=1;i<n;i++){if(q[i].x>last){ //如果当前区间的左端点比上一个区间的右端点要大，确定一个新的点，该点为当前区间的右端点sum++; //确定点数加1last = q[i].y; //修改last为新确定点的值，用于同下一个区间不叫}}printf("%d\n",sum);return 0;
}

6. 拼接最小数

题目描述
给定个可能含有前导0的数字串，将它们按任意顺序拼接，使生成的整数最小。

输入描述
第一行为一个正整数$n$（$1\le n\le 10^4$），表示数字串的个数。

第二行给出$n$个数字串（$1\le$每个串的长度$\le 9$），用空格隔开。

输出描述
输出一个整数，表示能生成的最小整数（需要去掉前导0）。

样例1
输入
3
53 01 2
输出
1253
解释
按01、2、53的顺序拼接，能得到最小整数1253。

下面是对这道题的解答：

贪心策略： 要使整数最小，只需优先选取字典序较小的字符数串作为整数的高位，字典序较大的字符数串放在低位。
注意，排序函数cmp要写成 return a + b < b + a，若如此写，假设a=120，b=12；a+b=12012，b+a=12120，那么，120会排在12的前面；如果写成return a<b，这会使得120排在12的后面，为了使得形成的整数串最小，120必须作为高位，12作为低位，因为12012<12120。
注：对于cmp函数，当return true时，string a排在string b的前面；当return false时，string a排在string b后面。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<map>
#include<set>
using namespace std;bool cmp(string a, string b) { //比较函数，字符串按字典序从小到大排序return a + b < b + a;
}int main() {int n, i, j;string s[10005];string str;cin >> n;getchar();for (i = 0; i < n; i++) {cin >> s[i];}sort(s, s + n,cmp); //对数字串按字典序从小到大排序for (i = 0; i < n; i++) {str.append(s[i]); //将排序后的数字串按序写入，形成整数串}i = 0;while (str[i] == '0' &&  i<str.length()) i++; //去除前导0if (i==str.length()) {//如果整数串全是0，现在已经成空串了cout<<"0"; //整数为0} else {for (j = i; j < str.length(); j++) { //输出去除前导0的整数cout << str[j];}}cout << endl;return 0;
}