python最小二乘估计模型OLS Regression Results含义解释

本文主要是介绍python最小二乘估计模型OLS Regression Results含义解释，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

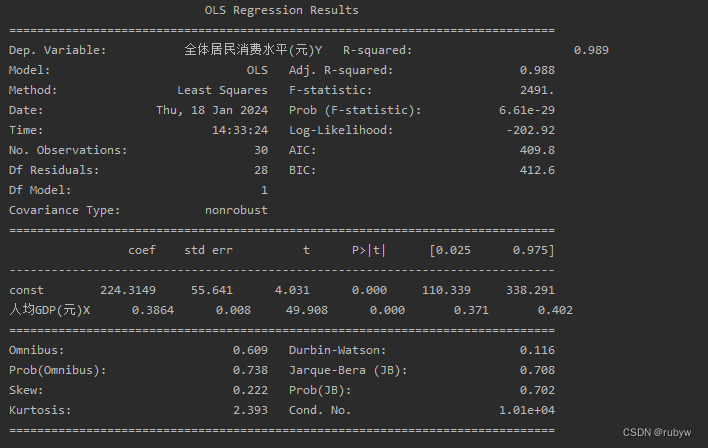
Log-Likelihood

对数似然性（Log-Likelihood）是在统计学中用于评估给定模型参数下观测数据的概率的一种方法。对数似然性的目标是最大化在给定数据条件下模型参数的可能性。

在一个概率模型中，给定观测数据，对数似然性（通常表示为LL或log-likelihood）可以通过以下步骤计算：

1. 定义概率分布：确定数据的概率分布，这通常由模型的选择决定。

2. 写出似然函数：似然函数表示在给定模型参数的情况下，观测到数据的概率。

其中，(n) 是观测数据的数量。

在Python中，对数似然性常常与最大似然估计（Maximum Likelihood Estimation，MLE）一起使用。在statsmodels等统计模型库中，模型拟合的结果通常包含对数似然性。

例如，在statsmodels中，可以通过以下方式获取对数似然性：

import statsmodels.api as sm# 假设已经有了模型对象 model
log_likelihood = model.llf
print(f"Log-Likelihood: {log_likelihood}")

对数似然性越高，表示模型在给定数据下的拟合程度越好。通常，对数似然性用于比较不同模型的拟合效果或进行模型选择。

AIC和BIC

AIC（赤池信息准则，Akaike Information Criterion）和BIC（贝叶斯信息准则，Bayesian Information Criterion）都是模型选择的信息准则，用于在多个模型之间进行比较，帮助选择最合适的模型。

AIC（赤池信息准则）:

AIC是由赤池弘次（Hirotugu Akaike）提出的信息准则，用于在估计的模型中平衡拟合优度和模型复杂度。AIC越小，模型越好。

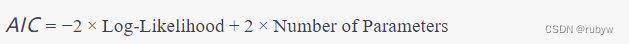
其中，Log-Likelihood是模型对数似然性，Number of Parameters是模型参数的数量。AIC的核心思想是用一个较小的惩罚项来纠正模型的参数数量对似然性的过度拟合。

BIC（贝叶斯信息准则）:

BIC是由斯瓦尔德（Gideon Schwarz）提出的信息准则，类似于AIC，但对参数数量的惩罚更强。BIC越小，模型越好。

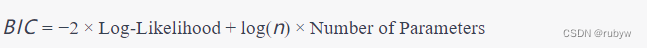
其中，(\log(n)) 是观测数据的数量的自然对数。BIC相对于AIC有一个更大的参数数量的惩罚，因此在选择模型时倾向于更简单的模型。

如何选择：

• AIC和BIC的比较：在比较不同模型时，通常选择具有最小AIC或BIC的模型，因为它们都是信息准则，越小越好。
• 权衡拟合和模型复杂性：AIC倾向于选择拟合更好的模型，而BIC倾向于选择更简单的模型。
• 具体问题：选择AIC还是BIC取决于具体的问题和分析目标。在实践中，可以查看两者的结果并综合考虑。

在Python的统计模型库（如statsmodels）中，拟合结果通常包含AIC和BIC的值，可以直接从模型结果中获取。例如：

import statsmodels.api as sm# 假设已经有了模型对象 model
aic = model.aic
bic = model.bicprint(f"AIC: {aic}")
print(f"BIC: {bic}")

这将输出模型的AIC和BIC值。

Jarque-Bera（JB）检验

目的：JB检验用于检验回归模型的残差是否符合正态分布。

正态性解释：
在线性回归中，我们通常假设误差项是正态分布的。如果残差不符合正态分布，可能影响对模型的统计推断。

JB检验解释：

JB统计量的计算基于残差的峰度（kurtosis）和偏度（skewness）。
JB统计量的取值越大，说明残差越不符合正态分布。
JB检验的假设为：
零假设（H0）：残差符合正态分布。
备择假设（H1）：残差不符合正态分布。
通常，如果JB统计量的p值低于显著性水平（例如0.05），则拒绝零假设，表示残差不符合正态分布。

在使用这些检验时，需要谨慎解释结果，并结合其他模型诊断方法，以确保模型的合理性和准确性。

Durbin-Watson（D-W）检验

目的：D-W检验主要用于检测回归模型中是否存在自相关性（Autocorrelation）。

自相关性解释：
自相关性表示误差项之间存在相关性，即残差并不是独立的。在回归分析中，我们通常假设误差项是相互独立的，如果存在自相关性，模型的参数估计可能不准确。

D-W检验解释：

D-W统计量的取值范围是0到4。
如果D-W统计量接近2，说明误差项之间基本不存在自相关性。
如果D-W统计量显著偏离2，可能存在自相关性。
D-W值接近0或4，表示存在较强的正向或负向自相关性。
通常，D-W检验的假设为：

零假设（H0）：误差项之间不存在自相关性。
备择假设（H1）：误差项之间存在自相关性。

Cond. No

Cond. No（Condition Number，条件数）是用于衡量矩阵在数值计算中的稳定性的一个指标。在线性回归分析中，条件数通常用于评估矩阵的病态性（ill-conditioning）。

条件数是通过矩阵的奇异值分解（Singular Value Decomposition，SVD）计算得到的。对于线性回归问题，条件数描述了输入特征矩阵的奇异值之间的比例。较大的条件数表示输入矩阵的奇异值之间的差异很大，可能导致数值不稳定性。

在线性回归的上下文中，条件数通常与多重共线性有关。多重共线性是指特征之间存在高度相关性的情况，这可能导致矩阵近似奇异，从而使得回归系数的估计变得不稳定。较大的条件数可能表明输入特征之间存在共线性。

在Python的numpy库中，可以使用以下方式计算条件数：

import numpy as np# 假设X是输入特征矩阵
X = np.array([[...], [...], ...])# 计算条件数
cond_number = np.linalg.cond(X)print(f"Condition Number: {cond_number}")

通常来说，较大的条件数可能表明输入矩阵存在数值不稳定性，需要关注是否存在多重共线性。较小的条件数通常表示较好的数值稳定性。

这篇关于python最小二乘估计模型OLS Regression Results含义解释的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---