本文主要是介绍UG手机支架建模,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近在学习3D建模,学校要求我们学习UG,但感觉网络上普遍是soidworks的教程居多,总想自己实践一下,这次就苟且使用Ug来复刻一个soidworks里常见的手机支架建模。
1. 绘制平面草图
首先需要在x -z平面上创建草图,如图是绘制完之后的样子:
画完之后大概长这样,但在绘制的时候我一开始总是出现问题,但经过后来的总结,在ug上绘制草图的时候要边绘制轮廓的同时就要尽可能地对线段等东西进行约束,不然画着画着草图就乱七八糟的了
2.对草图进行拉伸
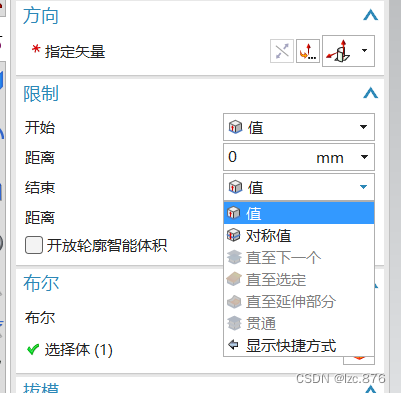
对草图进行拉伸时选择对称值,输入80mm

3.切割整体为梯形形状
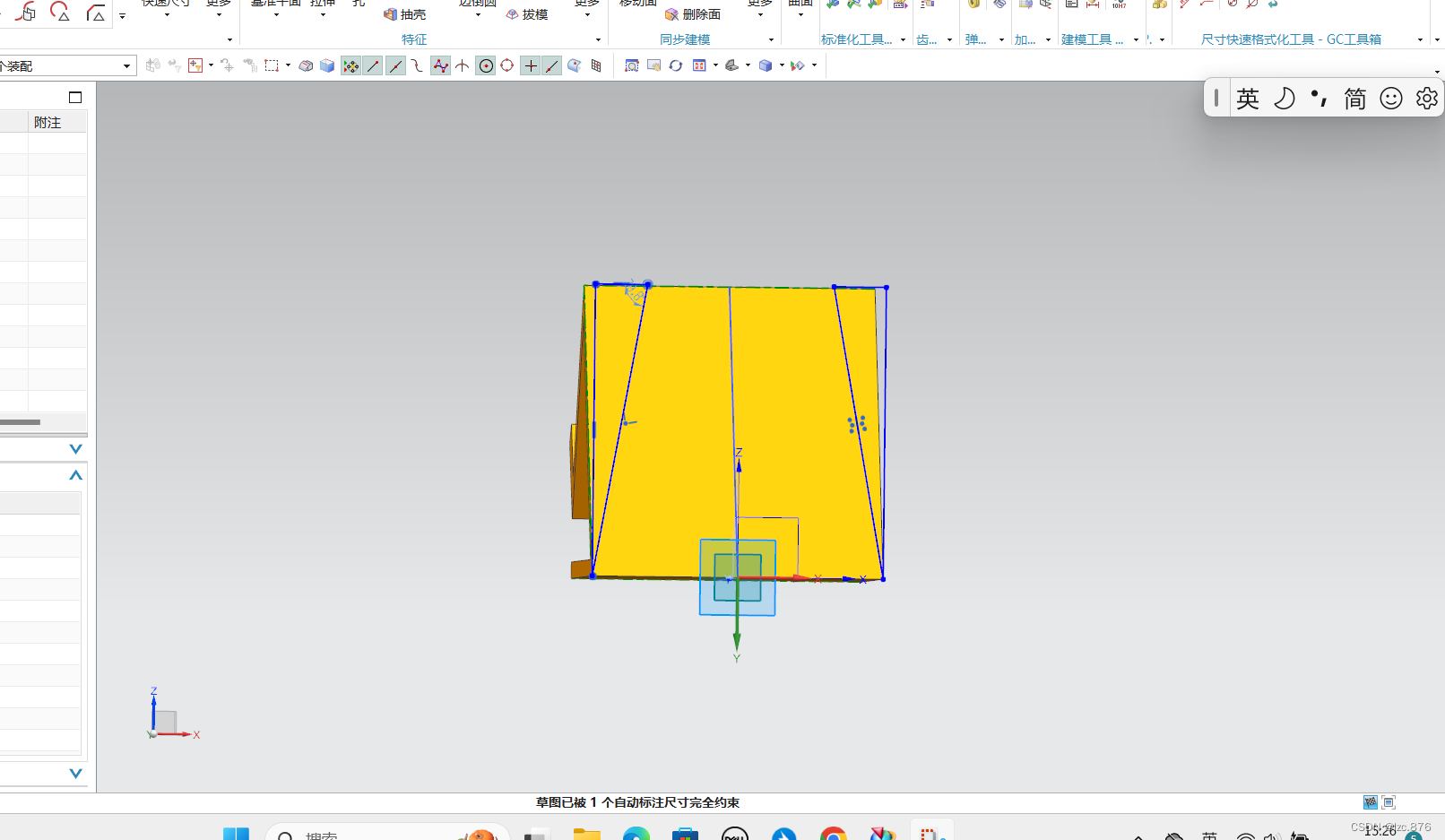
选定x-z面,来绘制草图,绘制两个封闭三角形轮廓(emm尺寸自己看着来吧)
之后再对画好的两个三角形轮廓进行拉伸,布尔值选择求差,拉伸的距离选择大一些,保证能和已有的实体相交。
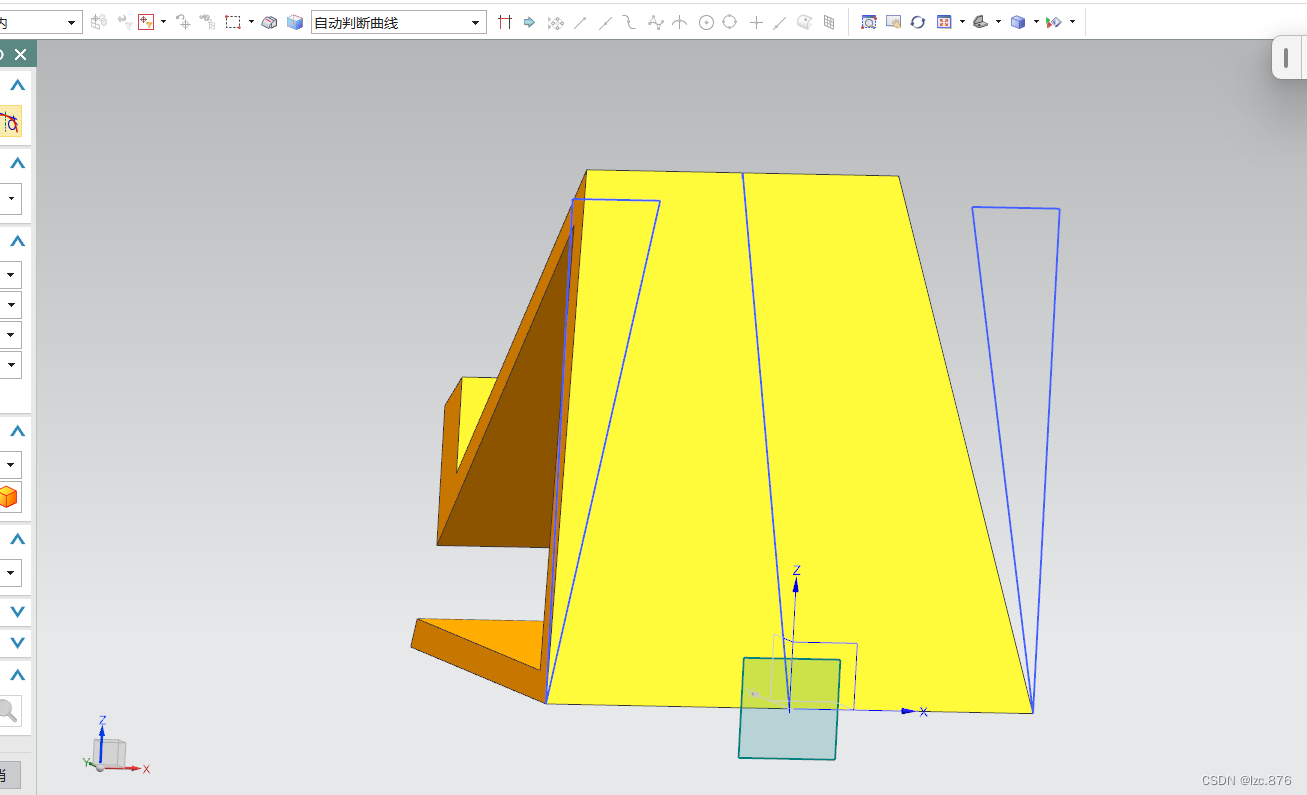
切割完之后就长这个样子了奥
4.切割手机充电口
继续绘制草图,记得在与手机相接触的一面绘制
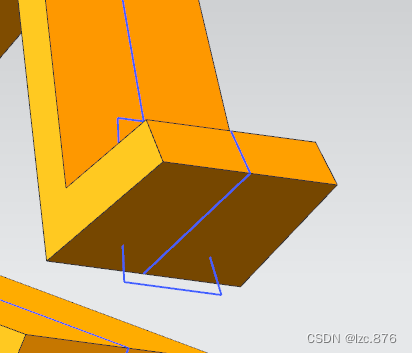
草图最好超出下边一些,再进行拉伸,布尔值仍然选择求差。

求差之后手机支架大概的形状就完成了,下面再来进行细节的修改。
5.倒角、圆角
选择边倒圆命令,对要倒角的边进行倒角即可
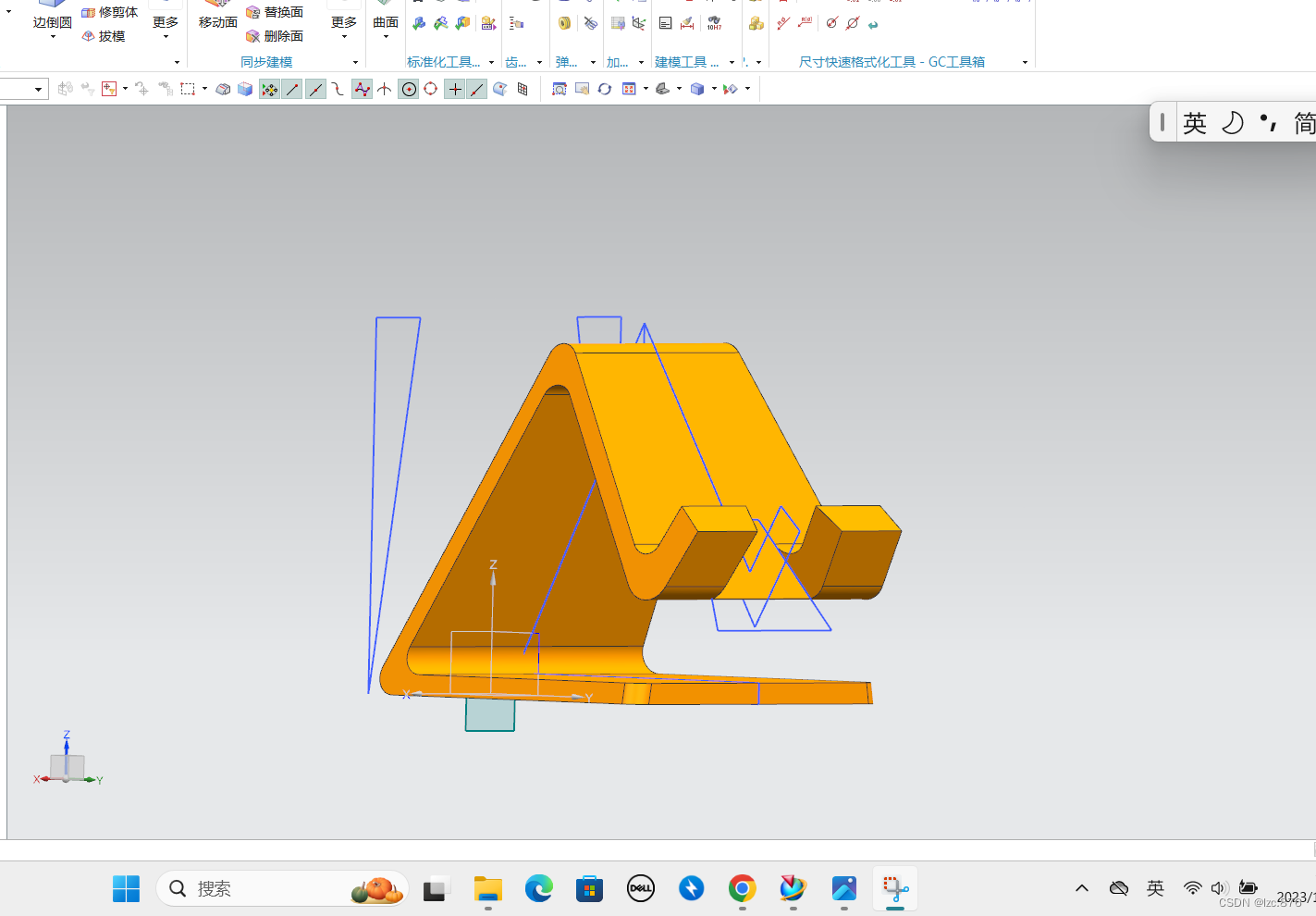
6.支架后侧挖孔

同样在背面绘制草图,拉伸选择求差,但这次选择的值不要过大,如果选择的值太大的话就切割到地面去了,这次我选择的是40mm。
7.给底面加支点
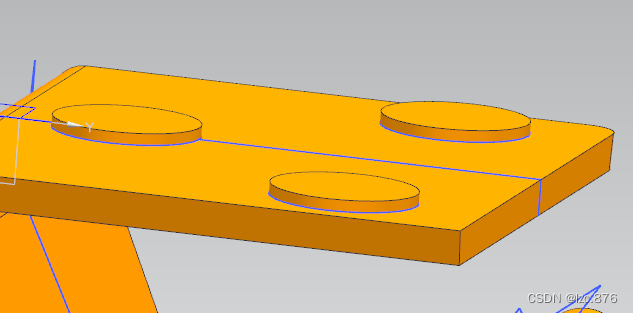
在底面画三个圆并拉伸,这次布尔值选择求和,别忘记改,之前用的都是求差。
画完就是这样了
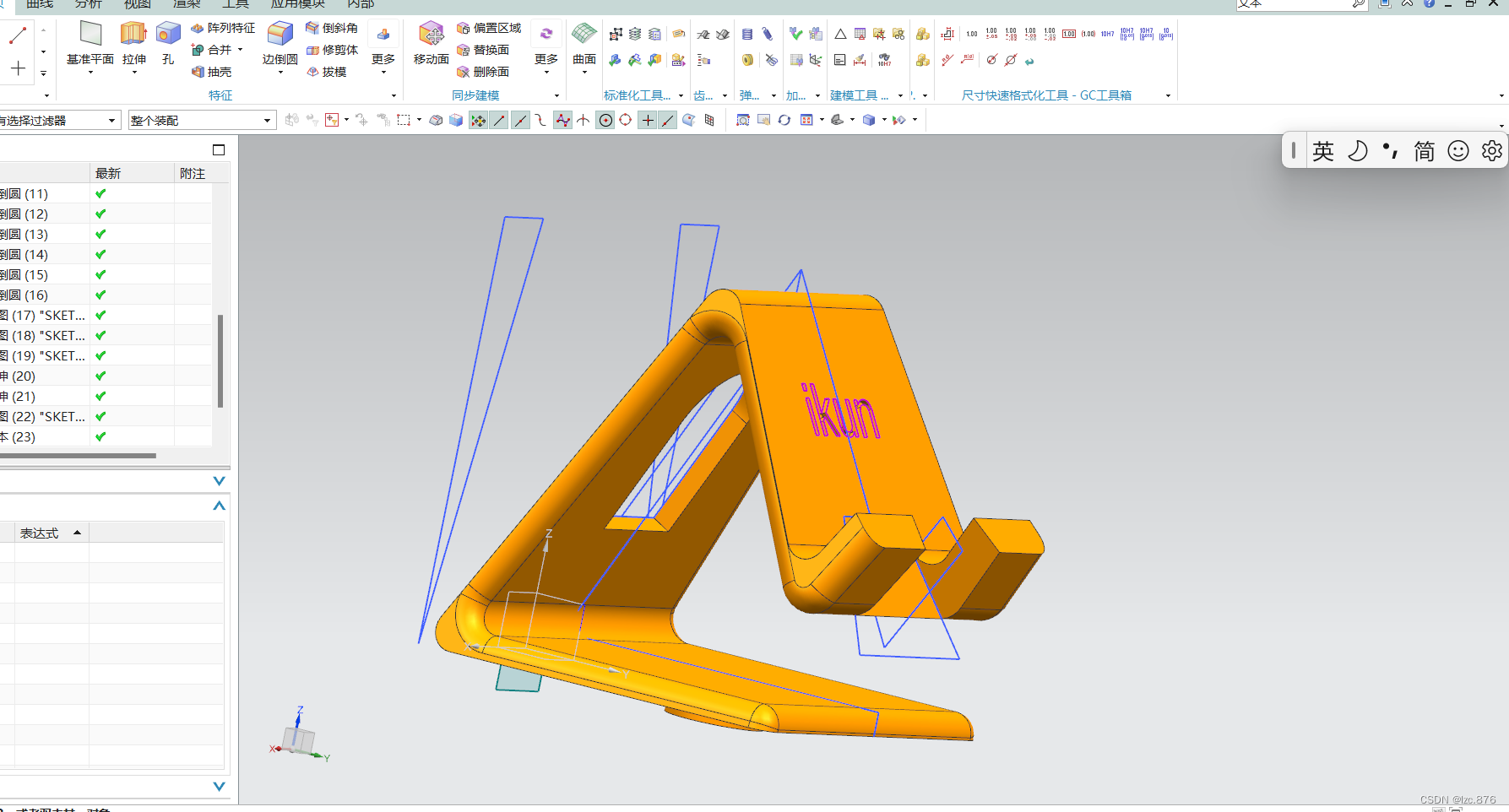
这篇关于UG手机支架建模的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







