SHI-TOMASI角点检测-opencv goodFeaturesToTrack函数

本文主要是介绍SHI-TOMASI角点检测-opencv goodFeaturesToTrack函数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

知道了什么是Harris角点检测，后来有大佬在论文《Good_Features_to_Track》中提出了它的改进版——Shi-Tomasi角点检测，Shi-Tomasi方法在很多情况下可以得到比Harris算法更好的结果。

Harris角点检测中每个窗口的分数公式是将矩阵M的行列式与M的迹相减：

由于Harris角点检测算法的稳定性和k值有关，而k是个经验值，不好设定最佳值。

Shi-Tomasi发现，角点的稳定性其实和矩阵M的较小特征值有关，于是直接用较小的那个特征值作为分数。这样就不用调整k值了。

所以Shi-Tomasi将分数公式改为如下形式：

和Harris一样，如果该分数大于设定的阈值，我们就认为它是一个角点。我们可以把它绘制到λ1～λ2空间中，就会得到下图：

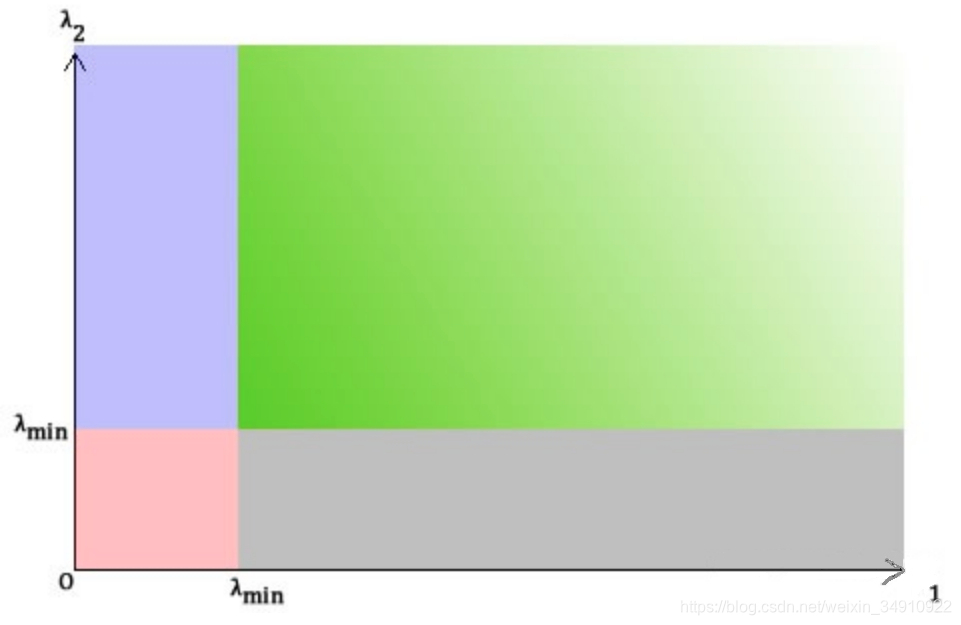
OpenCV提供了Shi-Tomasi的函数：cv2.goodFeaturesToTrack()，来获取图像中前N个最好的角点。函数原型如下：

goodFeaturesToTrack(image, maxCorners, qualityLevel, minDistance[, corners[, mask[, blockSize[, useHarrisDetector[, k]]]]])

其中的参数如下：

image：输入灰度图像，float32类型；

maxCorners：返回角点的最大数目，值为0表表示没有设置最大值限制，返回所有检测到的角点；

qualityLevel：质量系数（小于1.0的正数，一般在0.01-0.1之间），表示可接受角点的最低质量水平。该系数乘以最好的角点分数（也就是上面较小的那个特征值），作为可接受的最小分数；例如，如果最好的角点分数值为1500且质量系数为0.01，那么所有质量分数小于15的角都将被忽略；

minDistance：角之间最小欧式距离，忽略小于此距离的点；

corners：输出角点坐标；

mask：可选的感兴趣区域，指定想要检测角点的区域；

blockSize：默认为3，角点检测的邻域大小（窗口尺寸）；

useHarrisDetector：用于指定角点检测的方法，如果是true则使用Harris角点检测，false则使用Shi Tomasi算法。默认为False；

k：默认为0.04，Harris角点检测时使用。

设定好这些参数，函数就能在图像上找到角点。所有低于质量水平的角点都会被忽略，然后再把合格角点按角点质量进行降序排列。

然后保留质量最高的一个角点，将它附近（最小距离之内）的角点都删掉（类似于非极大值抑制），按这样的方式最后得到 N 个最佳角点。

python代码测试：

import cv2
import numpy as npdef test():max_corners = 100quality_level = 0.01min_distance = 10img = cv2.imread('test.jpg')img = cv2.resize(img, (512, 512))gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)corners = cv2.goodFeaturesToTrack(gray, max_corners, quality_level, min_distance)corners = np.int0(corners)for i in corners:x, y = i.ravel()cv2.circle(img, (x, y), 2, (0, 0, 255), -1)cv2.imwrite('out3.jpg', img)

结果：