二值图像分析–直线拟合与极值点寻找

在图像的处理中，会遇到一种情况，根据给定的点集（比如轮廓）拟合出一条直线的情景。

1.最小二乘法拟合直线

最小二乘法多项式直线拟合，根据给定的点，求出它的函数 $y=f(x)$，当然求得准确的函数是不太可能的，但是我们能够求出它的近似曲线 $y=\phi (x)$。

原理：
假如有点I = 1,2,3,……n,求近似曲线 $y=\phi (x)$，并且使得 $y=\phi (x)$与 $y=f(x)$的平方偏差和最小偏差:

现在有点（$x_1,y_1$)，($x_2,y_2$)···($x_n,y_n$)
设: 拟合多项式为：$y=ax+b$
平方偏差和如下：
$$e^2=\sum _{i=1}^n(y_i-y{)}^2=\sum _{i=1}^n(y_i-(ax+b){)}^2$$

其中我们要找到一组最好的a和b，“最好的”就是要使选出的a b能使得所有的误差达到最小化。所以上面得到的$e^2={\sum }_{i=1}^n(y_i-(ax+b){)}^2$就是一个关于a和b的函数。

2.多元函数极值与最值问题的理论依据

二元函数取极值的必要条件(类比一元函数)。

可以看到最小二乘法对各个变量求偏导，使得偏导值为0，即可得到最小值，因为e是关于a、b的函数，导数为0的点必定是最小值。
分别对a、b求偏导：

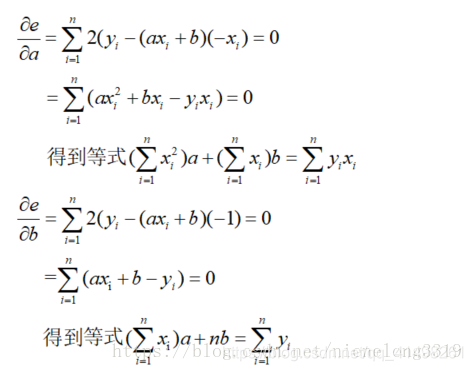
OpenCV中的API

• 说明
  使线拟合2D或者3D点集。

  函数fitLine通过最小化${\sum }_i\rho (r_i)$将线拟合到2维或3维点，其中$r_i$是第 $i^{th}$个点之间的距离，该线和$\rho (r)$是一个距离函数。

  该算法基于M-estimator技术，该技术使用加权最小二乘算法迭代拟合直线。每次迭代后，权重$w_i$被调整$\rho (r_i)$。

• 声明

  void fitLine(InputArray points, OutputArray line, int distType,double param, double reps, double aeps );
  

• 参数

  points	用于拟合直线的输入点集，可以是2维或者3维点向量。保存在std::vector<>或者Mat中。
  line	输出的直线。对于二维直线而言，类型为cv::Vec4f；对于三维直线类型，则为cv::Vec6f。输出参数的前半部分给出的是直线的方向，而后半部分给出的是直线上的一点（即通常所说的点斜式直线）。
  distType	距离类型。拟合直线时，要使输入点到拟合直线的距离和最小化，可供选择的距离类型如下，$r_i$表示的是输入的点到直线的距离。
  param	某些距离类型的数值参数（C）。跟所选的距离类型有关，值可以设置为0，cv::fitLine()函数本身会自动选择最优化的值如果为0。
  reps	半径的足够精度（坐标原点和直线之间的距离）。
  aeps	角度精度足够。对于reps和aeps，0.01将是一个很好的默认值。

  distType类型

  ① DIST_L2
  $$\rho (r)=r^2/2\text{(the simplest and the fastest least-squares method)}$$
  ② DIST_L1
  $$\rho (r)=r$$
  ③ DIST_L12
  $$\rho (r)=2\cdot (\sqrt{1+\frac{r^2}{2}}-1)$$
  ④ DIST_FAIR
  $$\rho \left(r\right)=C^2\cdot \left(\frac{r}{C}-\log \left(1+\frac{r}{C}\right)\right)\text{where}C=1.3998$$
  ⑤ DIST_WELSCH
  $$\rho \left(r\right)=\frac{C^2}{2}\cdot \left(1-\exp \left(-{\left(\frac{r}{C}\right)}^2\right)\right)\text{where}C=2.9846$$
  ⑥ DIST_HUBER
  $$\rho (r)=\{\begin{array}{ll}{r}^2/2& ifr<C\\ C\cdot (r-C/2)& otherwise\end{array}\text{where}C=1.345$$

应用

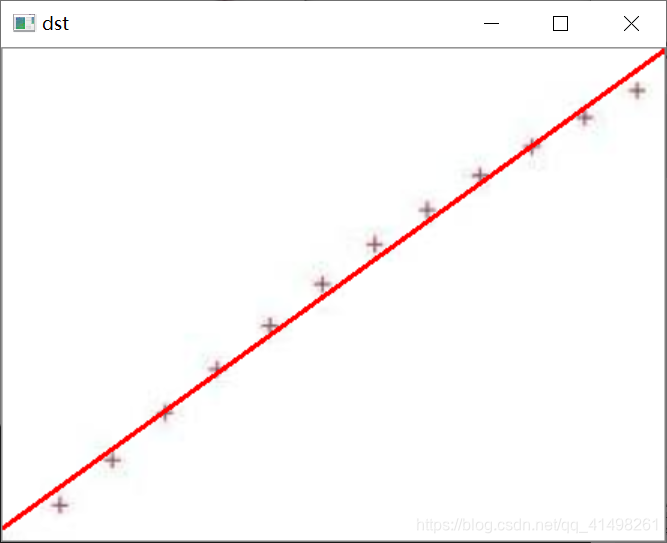
void apprixiLine() {//创建一个用于绘图的空白图Mat src = Mat::zeros(480, 640, CV_8UC3);//输入需要拟合的点vector<Point> points;points.push_back(Point(48, 58));points.push_back(Point(105, 98));points.push_back(Point(155, 160));points.push_back(Point(212, 220));points.push_back(Point(248, 260));points.push_back(Point(320, 300));points.push_back(Point(350, 360));points.push_back(Point(412, 400));//将拟合点画到空白画板上for (size_t i = 0; i < points.size(); i++){circle(src, points[i], 5, Scalar(0, 0, 255));}imshow("src", src);Vec4f line_para;fitLine(points, line_para, DIST_L2, 0, 1e-2, 1e-2);cout << "line_para: " << line_para << endl;Point point0;point0.x = line_para[2];point0.y = line_para[3];cout << "point0:[" << point0.x << "," << point0.y << "]" << endl;double k = line_para[1] / line_para[0];cout << "k=" << k << endl;//计算直线的端点Point point1, point2;point1.x = 0;point1.y = k * (0 - point0.x) + point0.y;point2.x = 640;point2.y = k * (640 - point0.x) + point0.y;cout << "point1:[" << point1.x << "," << point1.y << "]" << endl;cout << "point2:[" << point2.x << "," << point2.y << "]" << endl;line(src, point1, point2, Scalar(0, 255, 0), 2);imshow("dst", src);
}

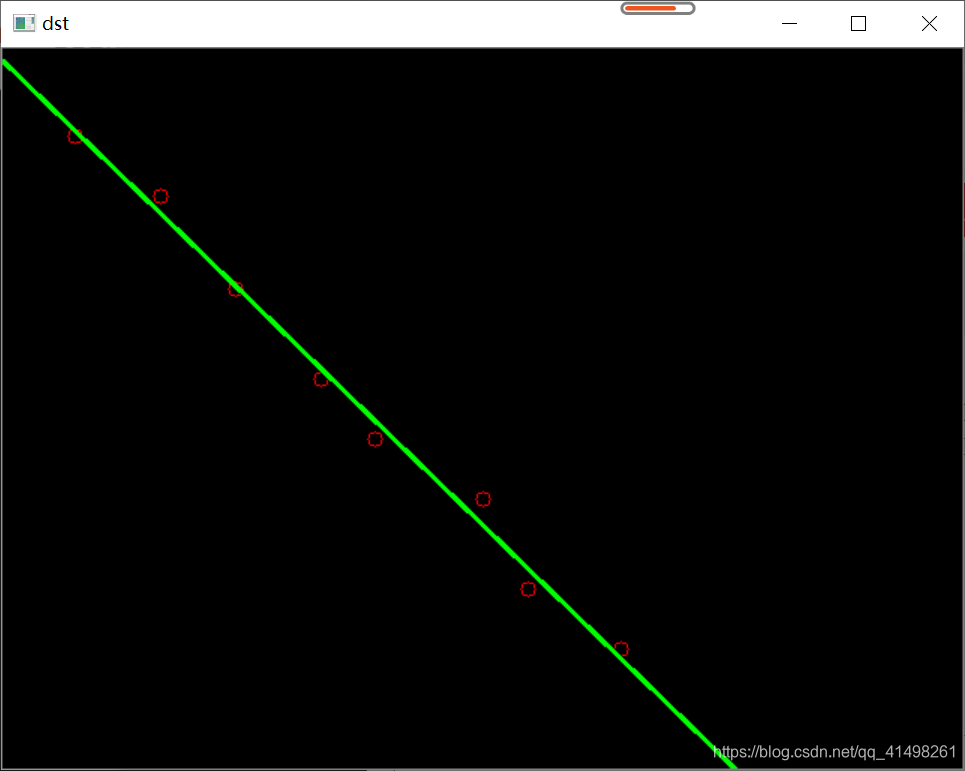
2. 事例二

void findFitLine(Mat& src) {//1. 转化灰度图像Mat gray;cvtColor(src, gray, COLOR_BGR2GRAY);//2. 二值化Mat binary;threshold(gray, binary, 0, 255, THRESH_BINARY | THRESH_OTSU);//3. 获得二维点集vector<Point> point_para;Point point_temp;for (size_t i = 0; i < src.rows; i++){for (size_t j = 0; j < src.cols; j++){if (binary.at<unsigned char>(i, j) < 255) {point_temp.x = j;point_temp.y = i;point_para.push_back(point_temp);}}}//4.直线拟合//拟合结果为4元素的容器，比如Vec4f-(vx,vy,x0,y0)//（vx、vy）是直线的方向向量//（x0、y0）是直线上的一个点Vec4f fitline;fitLine(point_para, fitline, DIST_L2, 0, 0.01, 0.01);//4.2 求出直线上的两个点double k = fitline[1] / fitline[0];Point p1(0, k * (0 - fitline[2]) + fitline[3]);Point p2(src.cols - 1, k * ((src.cols - 1) - fitline[2]) + fitline[3]);//4.3 显示拟合出的直线方程cout << "y-" << fitline[3] << "=" << k << "(x-" << fitline[2] << ")" << endl;line(src, p1, p2, Scalar(0, 0, 255), 2);imshow("dst", src);
}int main() {Mat src = imread("D:/test/fitline.png");if (src.empty()) {cout << " input the image error!" << endl;}imshow("src", src);findFitLine(src);waitKey(0);return 0;}

学习：

直线拟合——cv::fitLine()详解
【算法+OpenCV】基于opencv的直线和曲线拟合与绘制（最小二乘法）
opencv学习——最小二乘法拟合直线
OpenCV—直线拟合fitLine
【OpenCV3】直线拟合–FitLine()函数详解