瑞文考研算法每日一题—2023.05.24 环形链表 II

Problem: 142. 环形链表 II

方法一：哈希集合

思路

使用一个哈希集合记录链表中的所有结点，当遍历过程中如果出现重复元素，则说明链表中存在环，且当前结点即为环的第一个结点。若链表没有环，则集合无重复元素，最终返回null。

Code

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {set<ListNode*> set;while(head){if(set.count(head))return head;set.insert(head);head = head->next;}return nullptr;}
};

复杂度

• 时间复杂度:
  $O(n)$，n为链表长度

• 空间复杂度:
  $O(n)$，n为链表长度

方法二：快慢指针

思路

由环形链表的思路我们知道，可以通过快慢指针来判断链表是否存在环，但如何确定环的入口呢？
我们进行数学推导，由于快慢指针在环外不会相遇，它们在环的某一处相遇。此时假设环外距离为a，环内相遇处距离环入口b，剩余距离为c，同时快指针已经跑了n圈。

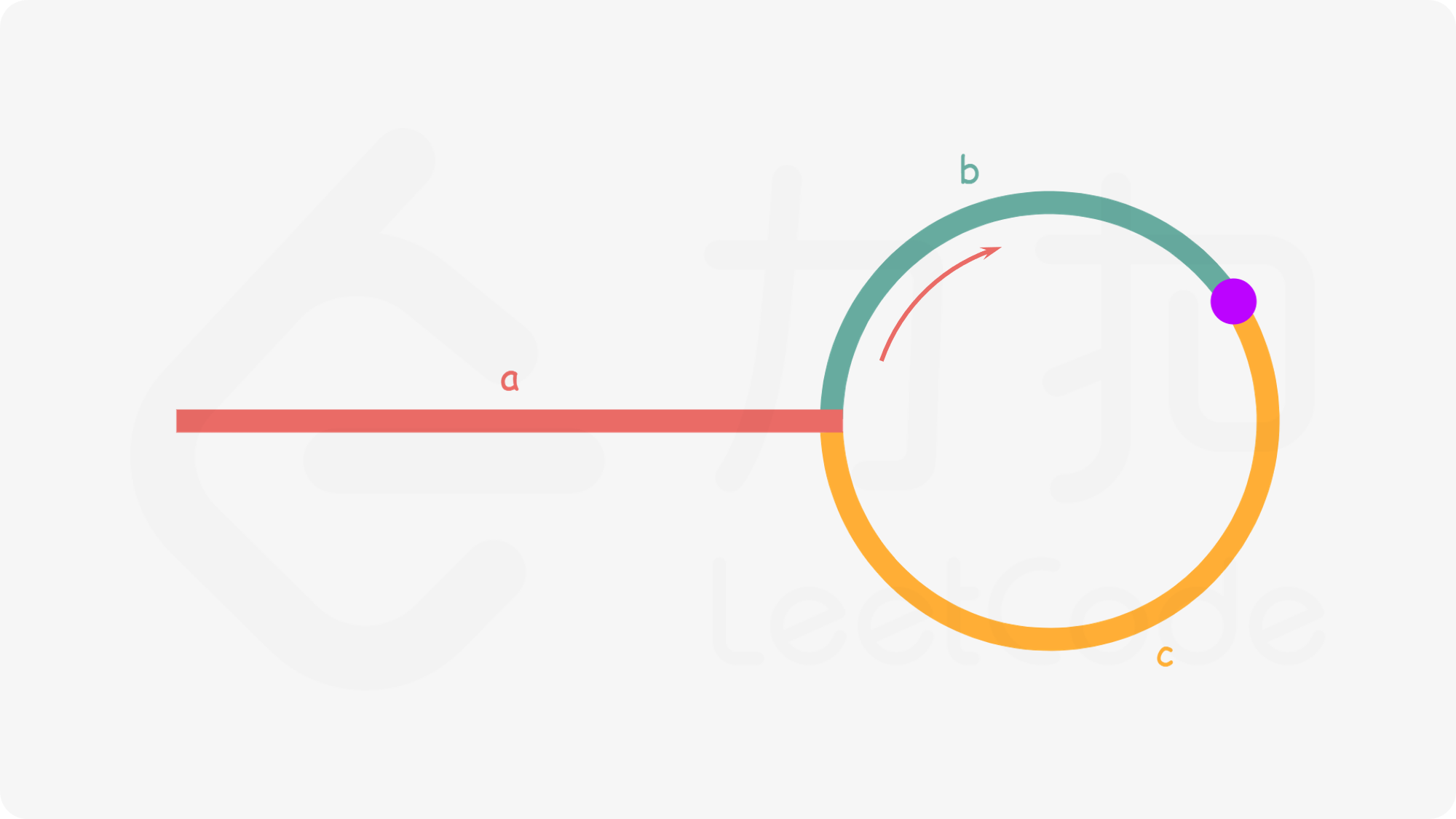
快指针：$ a + n(b + c) + b $

由于快指针的运动不是连续的，是跳跃的，慢指针是否也要跑多圈才会和快指针相遇呢？

答案是慢指针一定会在第一圈就和快指针相遇。假设慢指针刚刚进入环的入口，此时快指针一定在环内，距离环入口所在的慢指针x。x为圆的一段弧，小于等于圆的周长。此时使用相对运动来看问题（快指针的运动为连续的，每次前进一个结点），快指针与慢指针相对运动了x距离相遇，而此时慢指针又运动了距离环入口x的距离（快指针与慢指针的相对运动速度与慢指针的运动速度相同），而x是圆的弧，所以慢指针与快指针的相遇一定在第一圈。

慢指针：$ a + b$

由于快指针的速度是慢指针的2倍，且时间相同。联想距离公式$ s=vt $，距离也为2倍。
即 $ a + n(b + c) + b = 2 (a + b)$
整理得 $ a = (n - 1)(b + c) + c $
等式意义：头指针与慢指针以相同速度同时前进，它们会在环的入口处相遇

Code

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* slow = head, *fast = head;while(fast && fast->next){slow = slow ->next;fast = fast->next->next;if(slow == fast){while(head != slow){head = head->next;slow = slow->next;}return head;}}return nullptr;}
};

复杂度

• 时间复杂度:
  $O(n)$，n为链表长度

• 空间复杂度:
  $O(1)$