Surface-1 PCL学习记录-6 Moving Least Squares (MLS) （ 平滑处理-基于多项式拟合的法线估计+点云平滑和数据重采样）功能及用法解析

      曲面重建技术在逆向工程、数据可视化、机器视觉、虚拟现实、医疗技术等领域中得到了广泛的应用 。 例如，在汽车、航空等工业领域中，复杂外形产品的设计仍需要根据手工模型，采用逆向工程的手段建立产品的数字化模型，根据测量数据建立人体以及骨骼和器官的计算机模型，在医学、定制生产等方面都有重要意义 。

      除了上述传统的行业，随着新兴的廉价 RGBD 获取设备在数字娱乐行业的病毒式扩展，使得更多人开始使用点云来处理对象并进行工程应用 。 根据重建曲面和数据点云之间的关系，可将曲面重建分为两大类：插值法和逼近法。前者得到的重建曲面完全通过原始数据点，而后者则是用分片线性曲面或其他形式的曲面来逼近原始数据点,从而使得得到的重建曲面是原始点集的一个逼近曲面。

      关联知识：

      Search、KdTree、Octree 

      来源链接：http://robot.czxy.com/docs/pcl/chapter04/resampling/

 

一.基于移动最小二乘法(MLS)的平滑和法线估计

     问题来源：有时，测量较小的对象时会产生一些误差，这些误差所造成的不规则数据如果直接拿来曲面重建的话，会使重建的曲面不光滑或者有漏洞。而且，这些不规则的缺陷很难用统计分析的方法进行消除，所以为了建立完整并且可用的点云模型，必须对表面进行平滑处理和漏洞修复。在不能进行额外扫描的情况下（也就是仅依靠已有数据的情况下），可以通过对数据进行重采样来解决这一个问题。重采样的算法通过对周围数据点进行高阶多项式的插值来重建表面缺少的部分。（主要功能是平滑表面，重建不光滑和漏洞，以便后边查找法向正常）

    除此之外，多个扫描点的扫描结果配准后得到的数据直接拿来进行曲面重建会产生“双墙”等人造伪数据，即某快区域会出现重叠的两个曲面，使用重采样的方法同样可以处理这个问题。

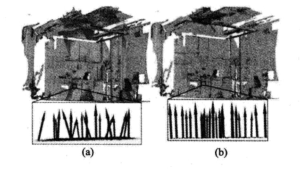
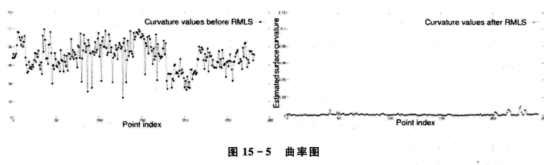
   实现例子：可以看到以下两个图片，分别表示的是两组点云数据配准后得到的数据集的表面法向估计的结果，由于配准造成的误差，可以看到左侧图片的发想值有非常严重噪声。右图是经过MLS点云平滑之后所得到的结果，明显比左侧图片准确很多。对比重采样前后的曲率特征方差很大，平滑后的方差相对较小。

二.使用体素网格进行降采样代码

//#include <ros/ros.h>
#include <iostream>
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/kdtree/kdtree_flann.h>
#include <pcl/surface/mls.h>
#include <pcl/io/io.h>
#include <pcl/visualization/cloud_viewer.h>int main(int argc,char ** argv){//MLS:MoveingLeastSquares(动态最小二乘法，后续查看API得知底层算法)//Step1:首先创建点云对象，并将PCD文件加载到点云文件中pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);pcl::io::loadPCDFile("bun0.pcd",*cloud); //注意，cloud是指针类型变量，要向指针内地址存数据，需要用*//Step2：由于MLS算法是基于KDTree实现的，所以需要创建KDTree对象pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);//Step3: 由于MLS功能包会同时计算点云的法向，因此创建一个用来存储包含法向信息的点云对象pcl::PointCloud<pcl::PointNormal> mls_points;//Step4：创建MLS对象/*注意！ MovingLeastSquares模板类的第一个参数：将要被处理的点云类型，在输出这个模板类的时候，点云XYZ内容将被平滑；第二个参数：输出只包含法线的点云。*/pcl::MovingLeastSquares<pcl::PointXYZ,pcl::PointNormal> mls;//Step5：设置是否使用多项式拟合提高精度mls.setPolynomialFit(true);//Step6: 使用MLS进行平顺mls.setInputCloud(cloud);mls.setPolynomialOrder(2);  //设置多项式的最高阶数为2阶？mls.setSearchMethod(tree);  mls.setSearchRadius(0.03);  //设置在进行Kdtree中K邻域，的查找半径mls.process(mls_points);//Step7:存储点云到PCD文件pcl::io::savePCDFile("bun0_mls.pcd",mls_points);std::cerr <<" MLS completed, please check the viewer and PCD file for detail." <<std::endl;//Step:Extra 显示点云pcl::visualization::CloudViewer viewer("Cloud Viewer");//这里会一直阻塞直到点云被渲染viewer.showCloud(cloud);// 循环判断是否退出while (!viewer.wasStopped()) {// 你可以在这里对点云做很多处理}return 0;
}

注意！以上例程输入的点云数据是pcl::PointXYZ格式的点云，而输出的是带有法向信息的pcl::PointNormal

效果如下（由于点云输入文件问题，处理后效果不是很明显，勉强能看到右侧的点云相较于左侧点云，略微平顺）