本文主要是介绍07、机器学习 （lineage回归分类算法与应用），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1. Lineage逻辑回归分类算法
1.1 概述
Lineage逻辑回归是一种简单而又效果不错的分类算法
什么是回归：比如说我们有两类数据，各有50十个点组成，当我门把这些点画出来，会有一条线区分这两组数据，我们拟合出这个曲线（因为很有可能是非线性），就是回归。我们通过大量的数据找出这条线，并拟合出这条线的表达式，再有新数据，我们就以这条线为区分来实现分类。
下图是一个数据集的两组数据，中间有一条区分两组数据的线。
显然，只有这种线性可分的数据分布才适合用线性逻辑回归
1.2 算法思想
Lineage回归分类算法就是将线性回归应用在分类场景中
在该场景中，计算结果是要得到对样本数据的分类标签，而不是得到那条回归直线
1.2.1 算法图示
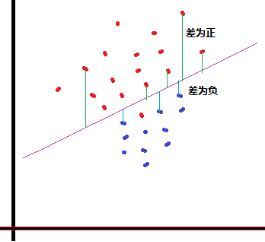
- 算法目标（）？
大白话：计算各点的y值到拟合线的垂直距离，如果
距离>0， 分为类A
距离<0， 分为类B
- 如何得到拟合线呢？
大白话：只能先假设，因为线或面的函数都可以表达成
y(拟合)=w1*x1 + w2*x2 + w3*x3 + ...
其中的w是待定参数
而x是数据的各维度特征值
因而上述问题就变成了 样本y(x) - y(拟合) >0 ? A : B
- 如何求解出一套最优的w参数呢？
基本思路：代入“先验数据”来逆推求解
但针对不等式求解参数极其困难
通用的解决办法，将对不等式的求解做一个转换：
- 将“样本y(x) - y(拟合) ”的差值压缩到一个0~1的小区间，
- 然后代入大量的样本特征值，从而得到一系列的输出结果；
- 再将这些输出结果跟样本的先验类别比较，并根据比较情况来调整拟合线的参数值，从而是拟合线的参数逼近最优
从而将问题转化为逼近求解的典型数学问题
1.2.2 sigmoid函数
上述算法思路中，通常使用sigmoid函数作为转换函数
- 函数表达式：
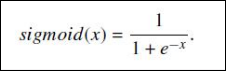注：此处的x是向量
- 函数曲线：
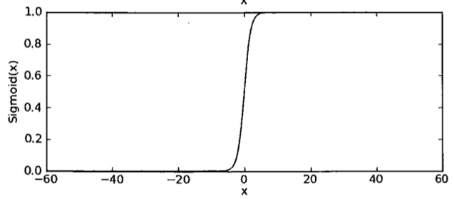
之所以使用sigmoid函数，就是让样本点经过运算后得到的结果限制在0~1之间，压缩数据的巨幅震荡，从而方便得到样本点的分类标签（分类以sigmoid函数的计算结果是否大于0.5为依据）
1.3 算法实现分析
1.3.1 实现思路
- 算法思想的数学表述
把数据集的特征值设为x1，x2，x3......
求出它们的回归系数wi
设z=w1*x1+w2*x2..... ，然后将z值代入sigmoid函数并判断结果，即可得到分类标签
问题在于如何得到一组合适的参数wi？
通过解析的途径很难求解，而通过迭代的方法可以比较便捷地找到最优解
简单来说，就是不断用样本特征值代入算式，计算出结果后跟其实际标签进行比较，根据差值来修正参数，然后再代入新的样本值计算，循环往复，直到无需修正或已到达预设的迭代次数
注：此过程用梯度上升法来实现。
1.3.2梯度上升算法
梯度上升是指找到函数增长的方向。在具体实现的过程中，不停地迭代运算直到w的值几乎不再变化为止。
如图所示：
2. Lineage逻辑回归分类Python实战
2.1 需求
对给定的先验数据集，使用logistic回归算法对新数据分类
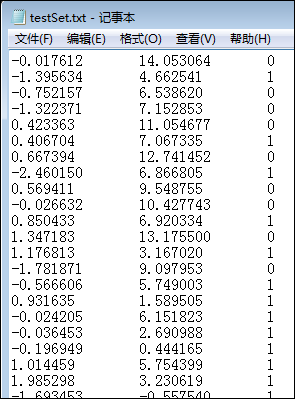
2.2 python实现
2.2.1定义sigmoid函数
| def loadDataSet(): dataMat = []; labelMat = [] fr = open('d:/testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat,labelMat
def sigmoid(inX): return 1.0/(1+exp(-inX)) |
2.2.2 返回回归系数
对应于每个特征值，for循环实现了递归梯度上升算法。
| def gradAscent(dataMatIn, classLabels): dataMatrix = mat(dataMatIn) #将先验数据集转换为NumPy 矩阵 labelMat = mat(classLabels).transpose() #将先验数据的类标签转换为NumPy 矩阵
m,n = shape(dataMatrix) alpha = 0.001 #设置逼近步长调整系数 maxCycles = 500 #设置最大迭代次数为500 weights = ones((n,1)) #weights即为需要迭代求解的参数向量
for k in range(maxCycles): #heavy on matrix operations h = sigmoid(dataMatrix*weights) #代入样本向量求得“样本y”sigmoid转换值 error = (labelMat - h) #求差 weights = weights + alpha * dataMatrix.transpose()* error #根据差值调整参数向量 return weights |
我们的数据集有两个特征值分别是x1，x2。在代码中又增设了x0变量。
结果，返回了特征值的回归系数：
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
我们得出x1和x2的关系（设x0=1），0=4.12414349+0.48007329*x1-0.6168482*x2
2.2.3 线性拟合线
画出x1与x2的关系图——线性拟合线
这篇关于07、机器学习 （lineage回归分类算法与应用）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
