BoyerMoore算法详解（理解不了你打死我）|代码实现（c++）

目录

1.BoyerMoore算法

1.1坏字符规则：

1.2好后缀规则

1.3一个例子

2.代码实现

1.BoyerMoore算法

BoyerMoore算法和KMP、BF算法一样，是一种字符串匹配的算法，不过它的效率比KMP算法更为高效（3~5倍）。

我们先来简单介绍一下BF算法的几个规则（特点）

1. 首先，将模式串和目标串（要进行查找的串）左端对齐，从右端开始比较。
2. 当比较的字符不匹配时，有两种规则。

1.1坏字符规则：

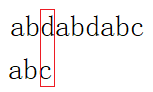
如上图：我们发现目标串的一个字符和模式串的对应的位置的字符不匹配，我们称这种现象为坏字符现象。这时我们首先在目标串中查找模式串中对应位置不匹配的字符的位置，简单的说，就是在abc中查找d，发现d不存在，我们记d在目标串中的位置为-1.然后用目标串不匹配的位置减去坏字符在目标串里出现的另一个位置（最右），如上2-（-1）=3(计数从0开始)，这时我们将目标串向右移动3，继续比较，这样的规则就是坏字符规则。

后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置
如果”坏字符”不包含在搜索词之中，则上一次出现位置为 -1。

再来一个例子让你理解：

再来：

P和E不匹配，P在目标串中上次出现的位置为4，移动距离为6-4=2.

上述就是坏字符规则，我们接着介绍好“好后缀规则”

1.2好后缀规则

看下图：

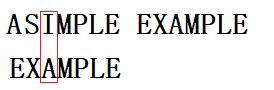
我们从后往前依次比较，发现MPLE都匹配上了，I和A没匹配上，这时如果我们按照上述的坏规则法，应该向向右移动（2-（-1）=3）个位置，移动后的结果为：

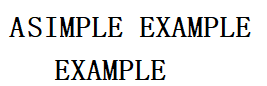
这时我们发现向后目标串只向后移动了三位。在这里我们介绍好后缀规则，这种规则能使目标串更快速的向后移动。

我们将两个字符串回归到下面这种状态：

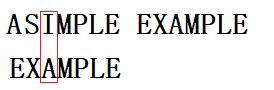
可以发现，后面的MPLE都配对上了，这时我们成PLE,LE,和E都为好后缀，这种我们称为好后缀现象。

好后缀规则就是：后移位数=好后缀出现的位置（以最后一个字符为准）-好后缀上一次出现的位置（除过后缀的最右边）

如果后缀不存在，那么记上一次的出现位置为-1.

我们发现只有后缀E在目标串里出现了两次，那么后移位数为：6-0 =6位。移动之后的状态为：

可以发现，比坏字符规则多移了三位。

需要注意的一点是：在Boyer-Moore算法中，并不是好后缀的移动距离一定大于坏规则的移动距离，当出现好后缀现象的时候，我们可以将好后缀的移动距离和坏规则的移动距离进行比较，取较大的来移动目标串。

再来一个例子：

我们假设匹配状态如下图：

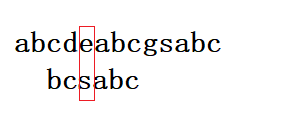
我们发现e和s不匹配，并且有好后缀abc,bc,c。

这时我们发现abc,bc,c都在前面出现了，这时候就可以解释为什么要以好后缀的最后一个字符为准的原因了。因为无论怎么多长的好后缀，它一定是以目标串的最后一个字符结尾的。即上述的好后缀都是以c结尾。所以我们可以直接以最后一个字符为参考值来确定好后缀规则的移动位数，这时移动位数应为：5 - 1 =4，移动之后如下图：

当然这个匹配最终是失败的，我们不要在乎那些只要明白好后缀的移动规则即可。

经过上面的这些说明，我们其实可以发现，如果末尾字符只出现在目标串的头和尾，或者只存在于末尾的话，那么每次好后缀规则向前移动的距离是相同的。

其实我们可以提前根据目标串确定坏字符表（存储坏字符规则的移动距离）以及好后缀表，好后缀表如下有几个例子。

xeapmple的后缀表应该为： （从右到左）8, 7, 7 ,7 ,7 ,7 ,7, 7, 8

example的后缀表应该为：6，6，6，6，6，7

abc的后缀表应该为：3，3，3（此时和坏规则一模一样）

pleple的后缀表应该为：3,3,3,3,6,6

我们其实可以发现，最末尾字符的坏规则移动距离和好后缀方法是一样的，这也算是这个算法的一个巧妙之处，每一次都会让目标串移动到确定的距离，且两种移动规则在某种条件下的移动距离是相同的。

1.3一个例子

介绍完上面两个规则，我们来看一个整体的匹配例子。（来源于阮一峰的分享）

第一步：

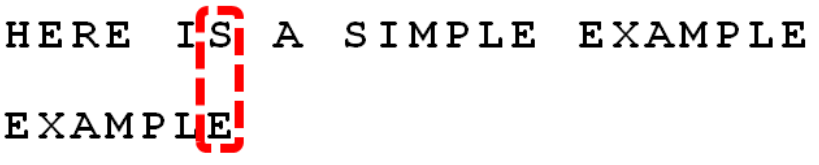
发现S和E不匹配，应用坏规则，向后移动6-（-1）=7位。

第二步：

P和E不匹配，且P在目标串中出现，后移位= 6-4 = 2

第三步：

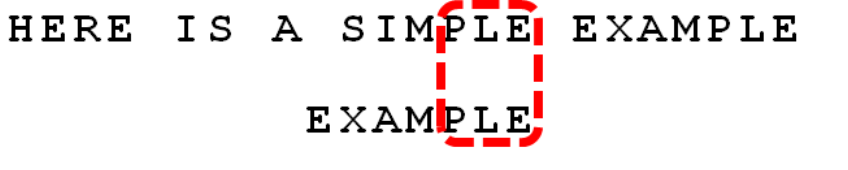
依次向前比较，发现I和A不匹配：

坏规则向前移动3位

好后缀向前移动6位

应用好后缀，向前移动6位。

第四步：

P和E不匹配，应用坏规则6-4=2位，向右移动二位。

第五步：

依次比较，匹配成功。

2.代码实现

如果我上面解释的还不够清楚，请看我的代码。

代码运行结果：

# include<iostream>
# include<string>
using namespace std;
//最长匹配长度
# define MAX_SIZE 1000//得到后缀规则的移动距离
int GoodSuffix(int j, string& pat) {int terminal = pat.length() - 1;int index = -1;j--;while (j >= 0) {if (pat[j] == pat[terminal]) {index = j;break;}else j--;}return terminal - index;
}
//得到坏字符规则的移动距离
int BadChar(int j,char temp,string str)
{int index = -1;for (int i = j - 1; i >= 0; --i){if (str[i] == temp){index = i;break;}}return j - index;
}
int BM(string source, string target)
{int i = 0, j = 0, soulen = source.length(), tarlen = target.length();  //初始化int badvalue = 0, distance = 0;if (soulen < tarlen) {  //比较长度printf("字符串的长度小于搜索词的长度\n");return -1;}i = tarlen - 1; j = tarlen - 1; //从尾开始匹配while (i < soulen) {if (source[i] == target[j]) {  //字符匹配成功if (j == 0) {printf("匹配成功\n");return i;}i--; j--;}else {  //未匹配成功if (j == tarlen - 1) {  //如果尾字符未匹配成功，"坏字符规则"badvalue = BadChar(j, source[i],target);cout << "坏字符移动：" << badvalue << endl;i = i + tarlen - 1 - j + badvalue;j = tarlen - 1;}else {  //有后缀,比较"坏字符规则"和"后缀规则"badvalue = BadChar(j, source[i], target);if (badvalue == -1)badvalue = target.length();distance = badvalue > GoodSuffix(j,target) ? badvalue : GoodSuffix(j, target);cout << "好后缀为：" << GoodSuffix(j, target) << "  坏字符为：" << badvalue << "  比较之后移动" << distance << endl;i = i + tarlen - 1 - j + distance;  //更新i的位置j = tarlen - 1;   //更新j位置}}}
}
int main()
{//好后缀表:存储了当遇到好后缀时，目标串向右的移动距离。int* goodSuffix = new int[MAX_SIZE];string model = "THERE IS A SIMPLE EXAMPLE";string str = "EXAMPLE";cout << "模式串" << model << endl;cout << "目标串" << str << endl;cout << str << "的好后缀表为：" << endl;for (int i = 0; i < str.length(); ++i){cout << str[i] << ":" << GoodSuffix(i,str) << endl;;}cout << "匹配成功的开始位置为：" << BM(model, str) << endl;delete[]goodSuffix;return 0;
}