评价最小二乘法回归模型的优劣用什么方法?_解决多重共线性之岭回归分析

上篇文章，我们介绍了几种处理共线性的方法。比如逐步回归法、手动剔除变量法是最常使用的方法，但是往往使用这类方法会剔除掉我们想要研究的自变量，导致自己希望研究的变量无法得到研究。因而，此时就需要使用更为科学的处理方法即岭回归。

岭回归

岭回归分析（Ridge Regression）是一种改良的最小二乘法，其通过放弃最小二乘法的无偏性，以损失部分信息为代价来寻找效果稍差但回归系数更符合实际情况的模型方程。

简单来说，岭回归是通过引入k个单位阵，使回归系数可以估计，得到的回归估计值要比简单线性回归系数更加稳定，也更加接近真实情况。虽然引入单位阵会导致信息丢失，但同时也换来回归模型的合理估计。

分析步骤

岭回归分析步骤共为2步：（1）结合岭迹图寻找最佳K值；（2）输入K值进行回归建模。

第一步：拖入数据，生成岭迹图，寻找最合适的K值。

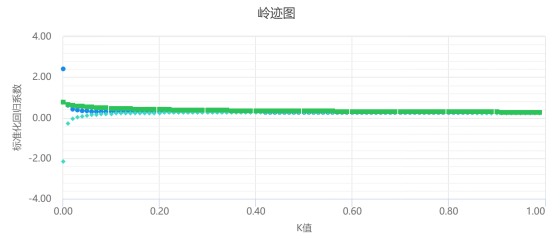
K值的选择原则是各个自变量的标准化回归系数趋于稳定时的最小K值。K值越小则偏差越小，当K值为0时则为普通线性OLS回归；SPSSAU提供K值智能建议，也可通过主观识别判断选择K值。

第二步：对于K值，其越小越好，通常建议小于1；确定好K值后，即可输入K值，得出岭回归模型估计，查看分析结果。

岭回归分析案例

（1）背景

现测得胎儿身高、头围、体重和胎儿受精周龄数据，希望建立胎儿身高、头围、体重去和胎儿受精周龄间的回归模型。根据医学常识情况（同时结合普通线性最小二乘法OLS回归测量），发现三个自变量之间有着很强的共线性，VIF值高于200；可知胎儿身高、体重之间肯定有着很强的正相关关系，因而使用岭回归模型。

（2）分析步骤

第一步：岭回归分析前需要结合岭迹图确认K值。首先拖拽身长、头围、体重到X分析框，胎儿受精周龄到Y分析框，不输入K值，SPSSAU会默认生成岭迹图，同时给出智能分析建议。

第二步：对于K值，其越小越好，通常建议小于1；本案例中K值取0.01，返回分析界面，输入K值，得出岭回归模型估计。

（3）输出结果

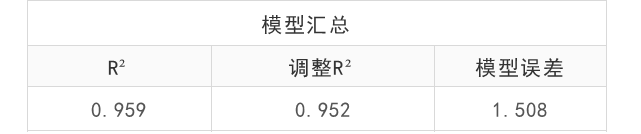
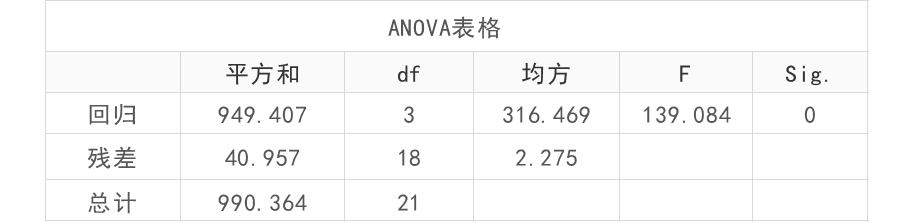
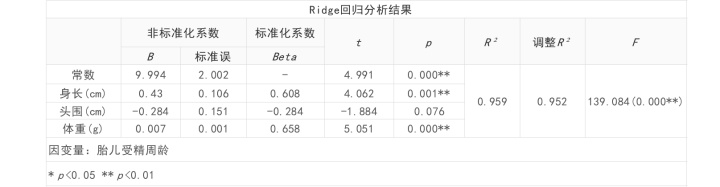
表1用于整体分析模型拟合情况，可以看出，模型R平方值为0.959，意味着身长(cm), 头围(cm), 体重(g)可以解释胎儿受精周龄的0.959变化原因，模型拟合程度好。

表2为岭回归ANOVA检验，用于判定模型是否有意义，本例中显示P值<0.05，说明模型有意义。

表3为岭回归分析结果，根据分析结果可知，模型公式为：胎儿受精周龄=9.994 + 0.430*身长(cm)-0.284*头围(cm) + 0.007*体重(g)。身长、体重通过显著性检验（P<0.05）说明对胎儿受精周龄有影响关系。

总结分析可知：身长(cm), 体重(g)会对胎儿受精周龄产生显著的正向影响关系。但是头围(cm)并不会对胎儿受精周龄产生影响关系。

其他说明

岭回归分析需要特别注意两点，分别是共线性判断和分析步骤。

• 是否呈现出共线性，一定需要有理有据，比如VIF值过高，也或者自变量之间的相关关系过高（比如大于0.6）；如果数据并没有共线性，依旧建议使用普通线性最小二乘法回归。
• 岭回归建模共分为两步，分别是寻找最佳K值和建模。岭迹图中，如果过了某点时趋于稳定，则该点对应的K值为最佳K值，以及K值是越小越好。

更多干货内容登录SPSSAU官网查看

SPSSAU：一图读懂：什么是偏相关？

SPSSAU：什么是虚拟变量？怎么设置才正确？

SPSSAU：多重共线性问题，如何解决？