【算法|滑动窗口No.4】leetcode 485.最大连续 1 的个数 487.最大连续 1 的个数 II 1004. 最大连续1的个数 III

本文主要是介绍【算法|滑动窗口No.4】leetcode 485.最大连续 1 的个数 487.最大连续 1 的个数 II 1004. 最大连续1的个数 III，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

个人主页：兜里有颗棉花糖
欢迎点赞👍 收藏✨ 留言✉ 加关注💓本文由兜里有颗棉花糖原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时，记录一下自己的学习过程，希望对大家有所帮助
🍓希望我们一起努力、成长，共同进步。

一、485.最大连续 1 的个数

原题链接：点击直接跳转到该题目

题目描述

给定一个二进制数组 nums ，计算其中最大连续 1 的个数。

示例1：

输入：nums = [1,1,0,1,1,1]
输出：3
解释：开头的两位和最后的三位都是连续 1 ，所以最大连续 1 的个数是 3.

示例2：

输入：nums = [1,0,1,1,0,1]
输出：2

提示：

1 <= nums.length <= $10^{5}$
nums[i] 不是 0 就是 1

解题代码

class Solution {
public:int findMaxConsecutiveOnes(vector<int>& nums) {int n = nums.size();int nums_0 = 0,ret = 0;for(int left = 0,right = 0;right < n;right++){if(nums[right] == 0) nums_0++;while(nums_0) {if(nums[left] == 0) nums_0--;left++;}ret = max(ret,right - left + 1); }return ret;}
};

二、487.最大连续 1 的个数 II

原题链接（会员题目）：点击直接跳转到该题目

题目描述

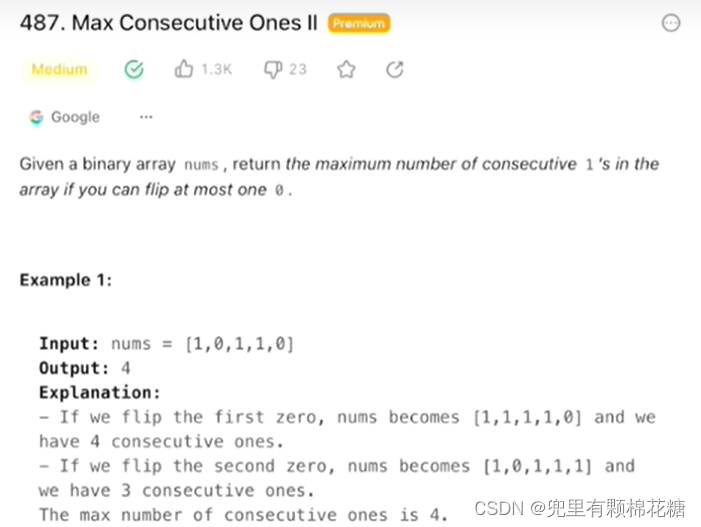
在这里插入图片描述

在这里插入图片描述
提示：

1 <= nums.length <= $10^{5}$
nums[i] 不是 0 就是 1

解题代码

class Solution {
public:int findMaxConsecutiveOnes(vector<int>& nums) {int n = nums.size();int nums_0 = 0,ret = 0;for(int left = 0,right = 0;right < n;right++){if(nums[right] == 0) nums_0++;while(nums_0 > 1) {if(nums[left] == 0) nums_0--;left++;}ret = max(ret,right - left + 1); }return ret;}
};

三、1004. 最大连续1的个数 III

原题链接：点击直接跳转到该题目

题目描述

给定一个二进制数组 nums 和一个整数 k，如果可以翻转最多 k 个 0 ，则返回数组中连续 1 的最大个数。

示例1：

输入：nums = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出：6
解释：[1,1,1,0,0,1,1,1,1,1,1]
粗体数字从 0 翻转到 1，最长的子数组长度为 6。

示例2：

输入：nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出：10
解释：[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗体数字从 0 翻转到 1，最长的子数组长度为 10。

解题代码

class Solution {
public:int longestOnes(vector<int>& nums, int k) {int n = nums.size();int nums_0 = 0,ret = 0;for(int left = 0,right = 0;right < n;right++){if(nums[right] == 0) nums_0++;while(nums_0 > k) {if(nums[left] == 0) nums_0--;left++;}ret = max(ret,right - left + 1); }return ret;}
};