本文主要是介绍算法分析与设计CH8:线性时间的排序——计数排序、基数排序、桶排序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
CH8:Sorting in linear time
Comparision Sort 比较排序:在排序的最终结果中,各元素的次序依赖于他们之间的比较。
任何的***比较排序**最好的最坏情况下经过 Ω ( n l g n ) \Omega(nlgn) Ω(nlgn)*次比较,归并,堆排都是最优的。
8.1 排序算法的下界
S o r t < a 1 , a 2 , a 3 , . . . , a n > Sort<a_1,a_2,a_3,...,a_n> Sort<a1,a2,a3,...,an>
判定树:Decision Tree
内部节点: i : j i:j i:j标识,满足 1 ≤ i , j ≤ n 1\leq i,j\leq n 1≤i,j≤n
叶子结点为一个排序序列: < Π ( 1 ) , Π ( 2 ) , . . . , Π ( n ) > <\Pi(1),\Pi(2),...,\Pi(n)> <Π(1),Π(2),...,Π(n)>
算法的执行对应一条从根节点到叶子结点的路径,每个内部节点标识一次比较 a i ≤ a j a_i\leq a_j ai≤aj。
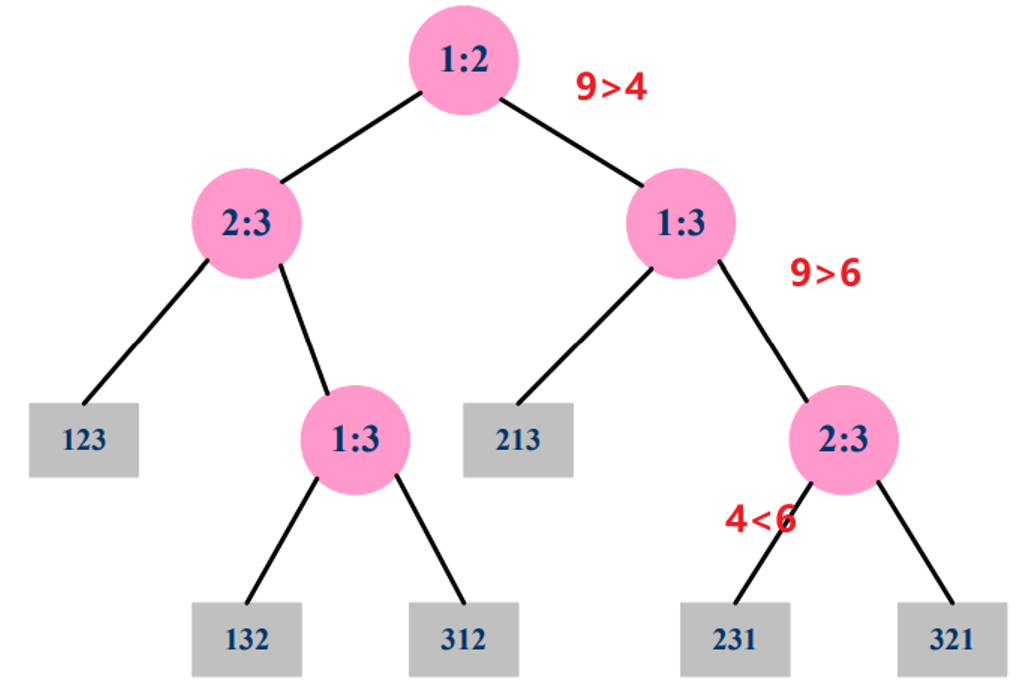
树包含所有可能出现的结果。
上树表示的是直接插入排序的结果。
从根节点到达任意一个可达叶子结点直接的最简单路径的长度:最坏情况下的比较次数。
所有情况:叶子数量为 n n n的全排列,即 n ! n! n!
h ≥ l g ( n ! ) ≥ l g ( n / e ) n = n l g n − n l g e = Ω ( n l g n ) h\geq lg(n!) \geq lg(n/e)^n\\ =nlgn-nlge=\Omega(nlgn) h≥lg(n!)≥lg(n/e)n=nlgn−nlge=Ω(nlgn)
归并排序和堆排序是渐进分析框架下的最优比较排序算法。
不可能比 Ω ( n l g n ) \Omega(nlgn) Ω(nlgn)更好
------------------------------------------>不靠比大小排序,数据具有特殊性
8.2 Counting Sort 计数排序
8.1.1 算法思路
输入:小范围内整数,重复值较多。数据范围为 [ 1 … … n ] [1……n] [1……n]
输出:另一个顺序数组 [ 1... n ] [1...n] [1...n]已排序
辅助数组:C[1…k]

算法思想:
- For x in A, if there are 17 elements less than x in A, then x belongs in output position 18.
- How if several elements in A have the same value? – Put the 1st in position 18, 2nd in position 19,3rd in position 20,…
- How if there are 17 elements not greater than x in A? – Put the last one in position 17, the penultimate one in position 16,…
利用数据特殊性,使用k个计数器。
vector<int> countingSort(vector<int>& vec, int k) {// 计数器初始化为全0 vector<int> C(k+1, 0); // 初始化计数器 vector<int> result = vec; // 初始化结果数组 // 统计等于该数的数据数量for (int i = 1; i < vec.size(); i++) {C[vec[i]]++; // 记录等于该值的元素 } // 统计小于等于该数的数据量 for (int i = 2; i <= k; i++) {C[i] += C[i-1]; // 记录小于等于该值的元素有多少个 }// 倒着扫描填表 for (int i = vec.size()-1; i >= 1; i--) { // 从原数组的最后一个开始向前扫描:保证稳定排序 result[C[vec[i]]] = vec[i]; // 三重嵌套,注意 C[vec[i]]--; // 使用一次减一回 }return result;
}
8.1.2 算法分析
(1)时间复杂度分析
该算法如果输入的数据是小范围的,k不超过n,那么时间复杂度为 Θ ( n ) \Theta(n) Θ(n),最坏情况下也是 Θ ( n ) \Theta(n) Θ(n)

(2)偏移考虑
数组范围:
- 如果范围是 0 … … k 0……k 0……k,那么计数器C[0]也使用即可
- 如果范围是 [ 2 … … k ] [2……k] [2……k],那么计数器 C [ 1 ] C[1] C[1]不用
- 如果范围是 [ 5000 … … 5100 ] [5000……5100] [5000……5100],那么计数器所有的 C [ v e c [ i ] − 偏移量 ] C[vec[i]-偏移量] C[vec[i]−偏移量]
// 给定某个范围,比如5000~5015
void counting_sort2(vector<int>& vec, vector<int>& result, int start, int k) { vector<int> counter(k - start + 1, 0); // 初始化为待排序数组的范围个0:0~k个0for (int i = 0; i < vec.size(); i++) {counter[vec[i]-start]++; // 等于vec[i]的个数 } for (int i = 1; i <= k - start; i++) {counter[i] += counter[i-1]; // 小于等于vec[i]的个数 }print(counter); for (int i = vec.size()-1; i>=0; i--) { result[counter[vec[i] - start]-1] = vec[i];counter[vec[i] - start]--;}print(counter);
}(3)扫描顺序
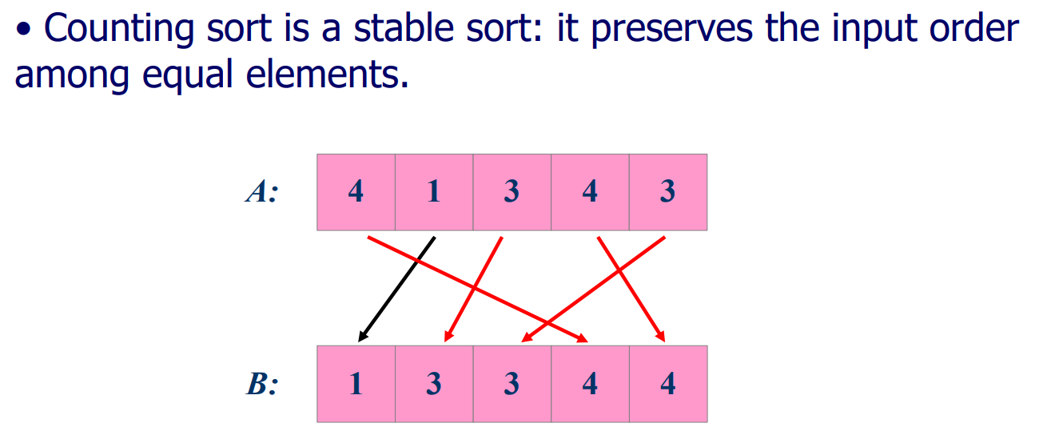
最后一步填入结果数组时,从原数组的最后向前扫描,保证稳定性。
8.3 Radix Sort 基数排序
8.3.1 算法思路
Digit by Digit Sort:按位排序
基数排序:使用辅助数组的稳定排序,首先对最低有效位进行排序
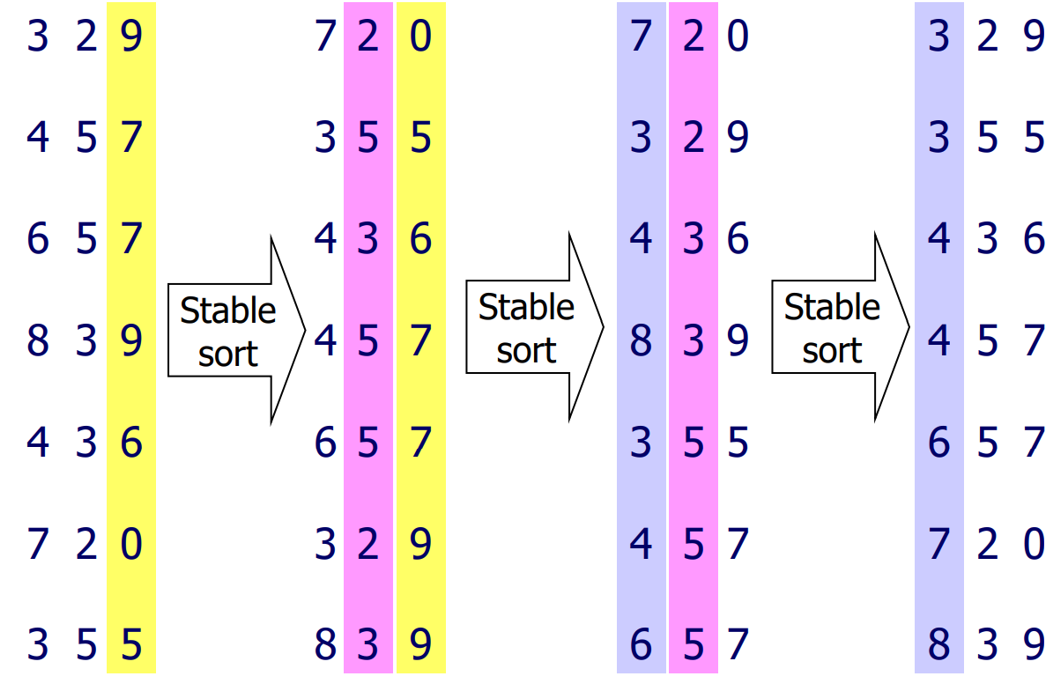
对每一位进行排序时使用的都是稳定排序,最后结果稳定。
RADIX-SORT(A, d)for (int i = 1; i <= d; i++) {do use a stable sort to sort array A on digit i; // 每一轮对某一位进行排序}
若位数不固定:采用最大的位数。
counting sort 合适。
8.2.2 时间复杂度分析
时间复杂度为 Θ ( d O ( n ) ) \Theta(dO(n)) Θ(dO(n)),其中 d d d是一个常数,时间复杂度为 Θ ( n ) \Theta(n) Θ(n)
8.4 BucketSort
8.4.1 算法思路
数据特殊性表现在:数据均匀分布。每个区间的数出现的概率相等。
(1)步骤
-
为每一个值分配一个桶
将 A [ i ] A[i] A[i]插入到桶 B [ ⌊ n A [ i ] ⌋ ] B[\lfloor nA[i]\rfloor] B[⌊nA[i]⌋]中,桶范围为 0 n − 1 0~n-1 0 n−1
映射关系保证,桶n-k内的数一定比桶n-k-r内的数大
-
对于每一个桶,内部使用直接插入排序
满足均匀分布,数字较少,插入排序可以认为为常数时间
-
将各个桶合并
常数时间

(2)算法实现
实际实现时桶的数据结构需要考虑用链表数组来实现。首先给出伪代码:

#include<iostream>
#include<algorithm>
#include<time.h>
#include<stdlib.h>using namespace std;class LinkNode{
public:double val;LinkNode *next;LinkNode() : val(0), next(nullptr) {};LinkNode(double x): val(x), next(nullptr) {}LinkNode(int x, LinkNode *next) : val(x), next(next) {}
};void printVec(vector<double>& vec) {for(int i = 0; i<vec.size(); i++) {cout << vec[i] << " ";if((i+1)%5 == 0) { // 控制打印,一行输出5个 cout << endl;}}cout<<endl;
}void random_generation(vector<double>& vec, int a, int b, int n) { // 产生a到b之间均匀分布的n个随机数 srand((unsigned int)time(NULL));for(int i = 0; i < n; i++) {double num = rand()*1.0/RAND_MAX; // 映射到0到1 num = num*(b-a) + a;vec.push_back(num);}} void bucket_sort(vector<double>& vec, vector<double>& res, int start, int end) {vector<LinkNode> linklist_vec;int n = vec.size();// 处理链表数组的头结点,头结点不放置数据for(int i = 0; i < vec.size(); i++) {linklist_vec.push_back(LinkNode(0)); } // 根据数值得到放置桶的下标 for (int i = 0; i<vec.size(); i++) {int index = floor(n*(vec[i] - start)/(end - start));LinkNode *head = &linklist_vec[index];while(head->next != nullptr and head->next->val<vec[i]) {head = head->next;}// 找到要插入的位置LinkNode* next_Pointer = head->next;head->next =new LinkNode(vec[i]);head->next->next = next_Pointer; }// 将非空桶中的数据取出,得到最终的顺序// 扫描并连接链表for(int i = 0; i < vec.size(); i++) {LinkNode *head = &linklist_vec[i];while(head->next != nullptr) {head = head->next;res.push_back(head->val);}}
}int main() {vector<double> vec;int start = 2, end = 5, n = 30;// 准备随机数 random_generation(vec, start, end, n);// 桶排序vector<double> res;bucket_sort(vec, res, start, end);printVec(res);
}
8.4.2 算法分析
算法的时间复杂度为 O ( n ) O(n) O(n),插入的时间和内部排序的时间都视作常数。

若区间不在0~1之间,那么要进行修改:
- [0~2]: B [ ⌊ n A [ i ] / 2 ⌋ ] B[\lfloor nA[i]/2\rfloor] B[⌊nA[i]/2⌋]
- [a, b]: B [ ⌊ n ( A [ i ] − a ) / ( b − a ) ⌋ ] B[\lfloor n(A[i]-a)/(b-a)\rfloor] B[⌊n(A[i]−a)/(b−a)⌋]
想一下怎么把这个数变到0~1就行了。
8.5 总结
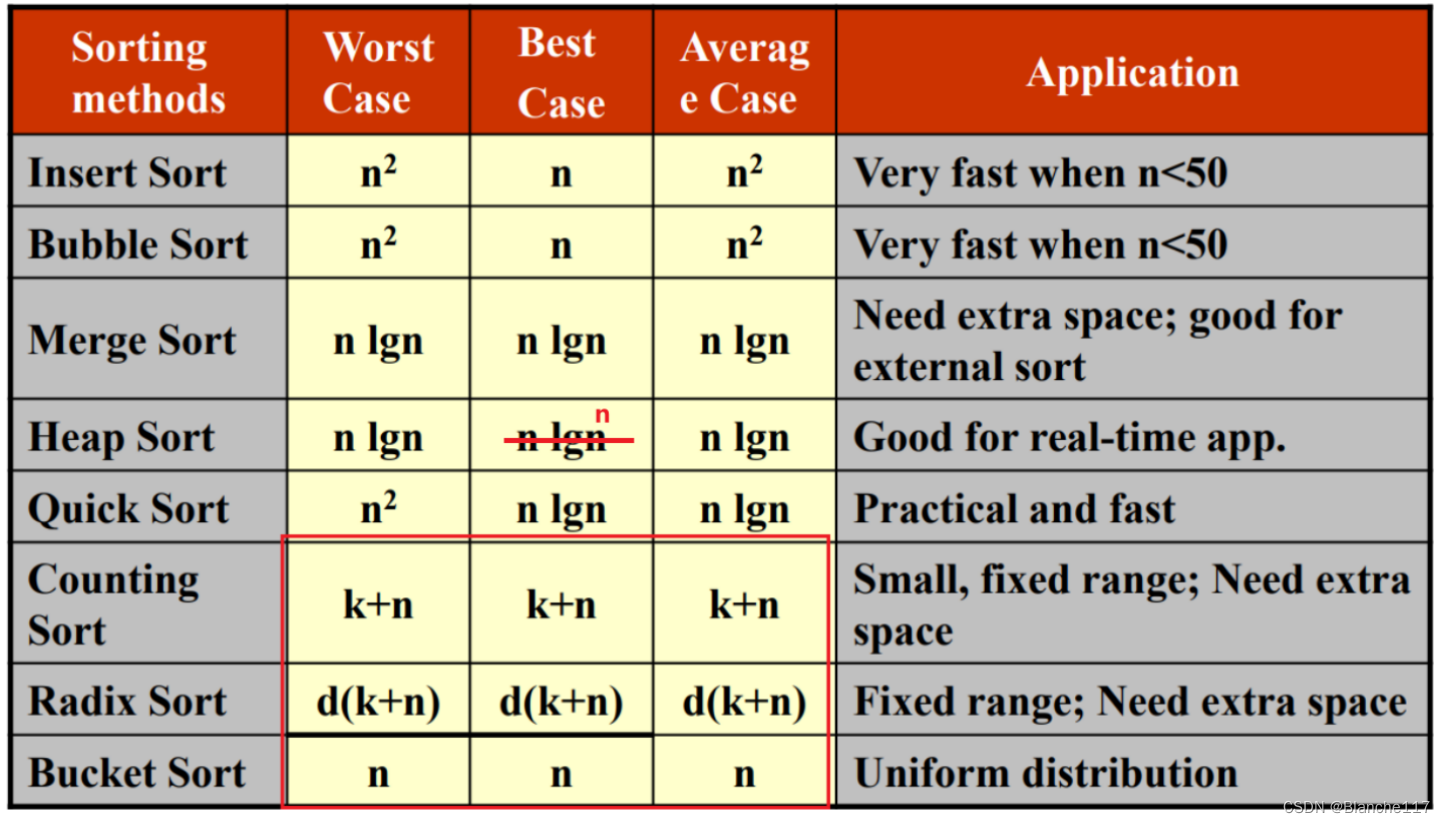
这篇关于算法分析与设计CH8:线性时间的排序——计数排序、基数排序、桶排序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







