No.01 正交不平衡补偿 GSOP算法有MATLAB和Python代码实现

本文主要是介绍No.01 正交不平衡补偿 GSOP算法有MATLAB和Python代码实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

理解难点：

区分不平衡和不正交的概念。
正交归一化并非绑定在一起，正交是必须要处理的，至于是否归一化随性而定。
建议将 IQ 不平衡的原因与导致的现象之间的数学推导熟悉一遍，有助于理解。

正交不平衡的原因和表象

在理想情况下，相干探测得到的 I 路和 Q 路信号是完全正交的，但实际实验中有多种原因会造成 IQ 两路不平衡，从而破坏 IQ 两路的正交性，导致系统性能恶化，还会影响后续 DSP 模块正常工作。造成此现象的原因主要是调制器和接收机的不理想。

调制器的不理想主要体现在，调制器 IQ 两路偏置点设置的不正确，3dB耦合器分光比不对称，90°正交偏置电压设置不准确。接收机的不理想主要体现在，3dB 耦合器分光比不对称，90°光混频器的不完美，光电二极管响应率不匹配。除了这些主要原因外，还有一些次要因素。如，输入调制器的两臂的 IQ 信号由于电放大器的工艺问题，导致驱动幅度不一样。以及偏振控制的失调等等。这些因素并没有那么重要，并且也可以通过 IQ 不平衡补偿一并处理掉，就不一一列举了。

由上述多种原因联合作用，最终体现在信号上的现象表现为三个方面：

I 路或 Q 路的幅值分布不均匀
I 路或 Q 路的幅值分布中心点不统一
I 路与 Q 路信号不正交

由此可以知道，所谓 IQ 不平衡与不正交是包含与被包含的关系。上述幅值中心点和分配不均都可以通过判决门限的选定来解决。比较麻烦的是不正交的问题，无论问题出在收端还是发端，都会使得 IQ 两路的信息相互耦合。

Gram-Schmidt 正交化过程

Gram-Schmidt 正交化过程 (Gram-Schmidt Orthogonalization Procedure, GSOP) 是解决 IQ 不平衡的经典算法。
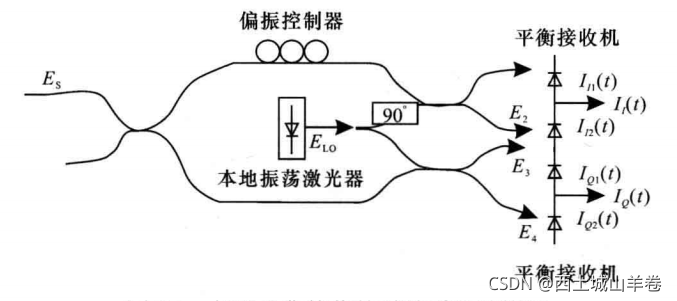
在这里插入图片描述

理想情况下，经上图平衡探测相干接收后输出的信号为：
$\left\{ \begin{aligned} & I_I(t)\propto Re\{E_sE^*_{lo}\} \\ & I_Q(t)\propto Im\{E_sE^*_{lo}\} \end{aligned} \right.$
GSOP 将 IQ 不平衡问题建模为：
$\left\{ \begin{aligned} & I_I(t)\propto Re\{E_sE^*_{lo}\} \\ & I_Q(t)\propto \alpha \cdot Im\{E_sE^*_{lo}\cdot e^{j\theta}\} \end{aligned} \right.$

GSOP 算法认为 Q 路混入的 I 路的信息。如果你做过 IQ 不平衡原因与现象之间具体的数学推导，就可以看出这种建模方式是值得改进的。

我要做的工作是恢复采样信号 $I_I(k)=\{I_I(1), I_I(2), ..., I_I(n)\}$ 和 $I_Q(k)=\{I_Q(1), I_Q(2), ..., I_Q(n)\}$ 的正交性，并做归一化。

从简单的例子入手，我有两个f非正交二维向量 $A, B$ ，几何直观能够很好理解：
在这里插入图片描述

只需要让 A 对 B 做垂线，得到的向量 C 就和 B 是正交的了。于是用 C 代替了 A 。
IQ 两路信号只不过是维度更高，原理上完全一致。

$\begin{aligned} & I_{out}(k)=\frac{I_I(k)}{\sqrt{E[I^2_I(k)]}}\\ & Q_{out}(k)=\frac{I_Q(k)-E[I_I(k)I_Q(k)]\frac{I_I(k)}{E[I^2_I(k)]}}{\sqrt{E[I^2_Q(k)]}} \end{aligned}$

这里把 Q 路信号投影到了 I 路，并对功率做了归一化。

从处理方式可以看出，GSOP 算法解决了不正交的问题，但这种对不正交性的建模是不准确的。另外还通过归一化解决了信号幅度范围不相同的问题，但并没有解决幅度分配不均以及中心点设置不相同的问题。

代码实现

大家应该都用这同一个代码来实现 RSOP 算法

function output = gsop(input)
%GSOP IQ不平衡补偿算法rI = real(input);rQ = imag(input);rho = mean(rI.*rQ);PI = mean(rI.*rI);PQ = mean(rQ.*rQ);Iout = rI/(sqrt(PI));Qout0 = rQ-rho*rI/PI;Qout = Qout0/sqrt(PQ);output = Iout+1i*Qout;% scatterplot(output);
end

为什么非要自己造轮子呢？咱们用用 SymPy 库不香嘛
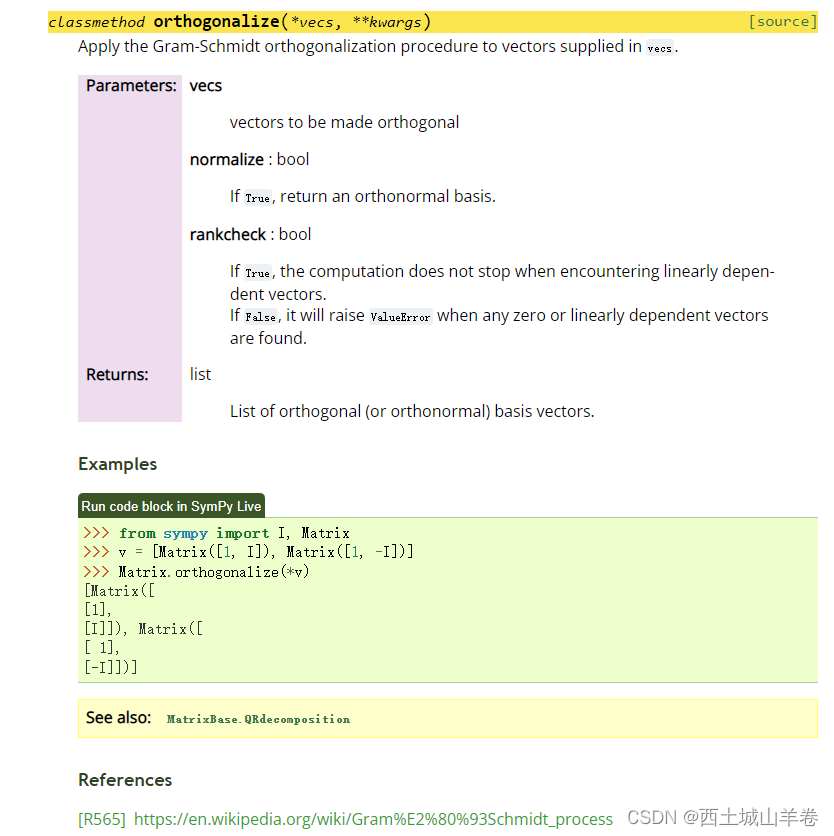
在这里插入图片描述