Python代码实现：坐标轮换法求解多维最优化问题

多维最优化问题

此前介绍的黄金分割法和切线法都是针对一维最优化问题的解决方案。本文开始，我们将最优化问题从一维扩展到多维，暂时仍考虑无约束的优化场景。

坐标轮换法原理

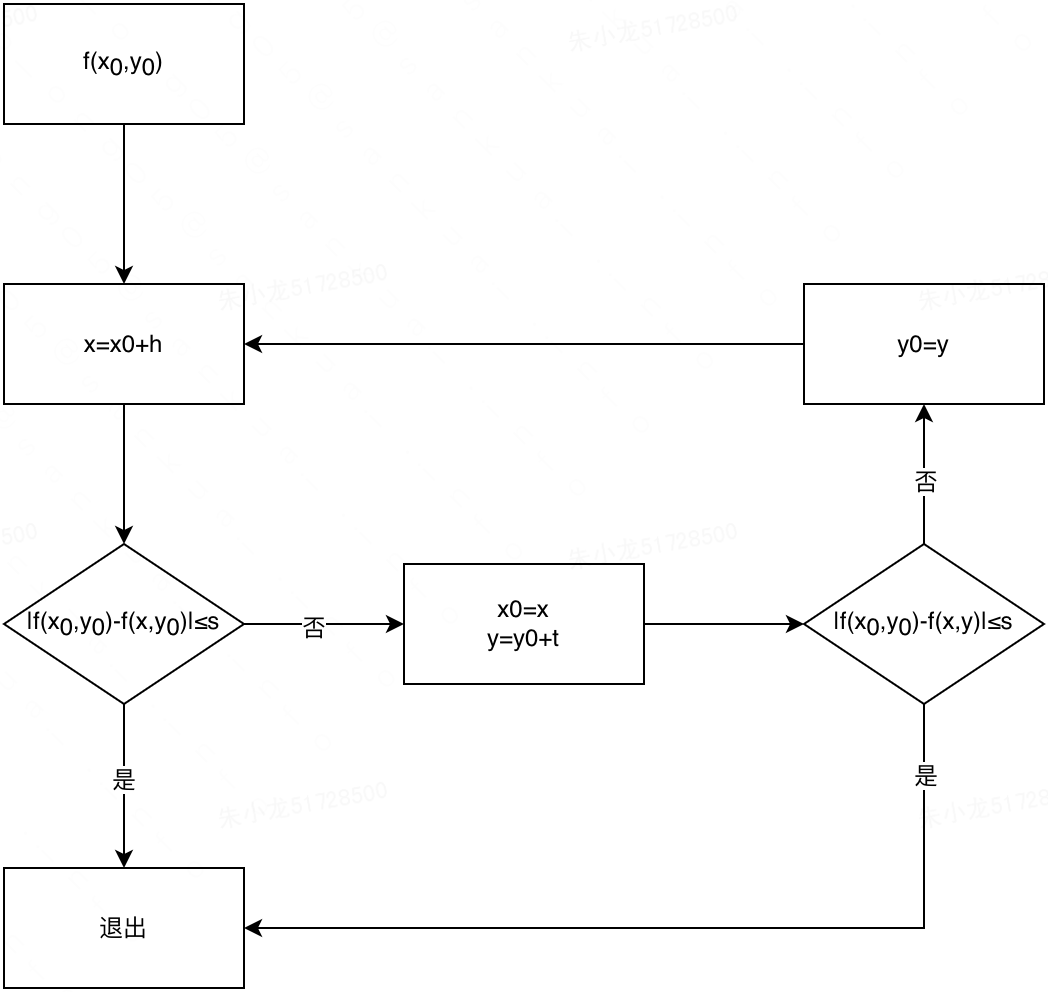
问题维度扩展后，很容易想到的一个解决方案就是先将多维问题降维至一维，然后再使用之前的算法依次求解。坐标轮换法就是基于该思路所设计的一个算法，其实现流程（假设问题为2维最小化问题，更高维度可以直接类推）为

1. 选取初始值$f(x_0,y_0)$。
2. 沿着$x$轴搜索，得到局部最优解：$x=x_0+h$。
3. 判断解的优化程度是否超出阈值$s$：如果小于$s$，直接退出；反之，继续执行第4步。
4. 沿着$y$轴搜索，得到局部最优解：$y=y_0+t$。
5. 判断解的优化程度是否超出阈值$s$：如果小于$s$，直接退出；反之，跳转执行第2步。

其中，第2步和第4步中局部最优解的求解均为一维最优化问题，其计算过程为：先使用进退法确定搜索区间，然后在该区间使用黄金分割法计算最优解。

下图为坐标轮换法的示意图。

代码实现坐标轮换法

以下以二维函数的最小化问题为例，使用Python实现了坐标轮换法。挺尴尬的，代码水平有限，两个方向的计算，进退法和黄金分割法分别使用了两个函数，所以主要关注一下逻辑吧。当然了，这么差的水平，也没必要再用Java写一遍了，以后代码水平提升后再做补充。

# 待优化函数f
def f(x, y):return 2 * x**2 + 3 * y**2 - 8 * x + 10# 待优化函数g
def g(x, y):return 4 + 4.5 * x - 4 * y + x * x + 2 * y * y - 2 * x * y + x**4 - 2 * x * x * y# 进退法：确定搜索区间，x方向
def advance_and_retreat_x(func, x, y, h):if abs(func(x, y) - func(x + h, y)) <= 1e-6:# 第三种情况x_min, x_max = x, x + helif func(x, y) < func(x + h, y):# 第一种情况x_max = x + hlamb = 1while func(x - lamb * h, y) < func(x, y):lamb += 1x_min = x - lamb * helse:# 第二组情况x_min = x + hlamb = 2while func(x + lamb * h, y) < func(x + h, y):lamb += 1x_max = x + lamb * hreturn x_min, x_max# 进退法：确定搜索区间，y方向
def advance_and_retreat_y(func, x, y, h):if abs(func(x, y) - func(x, y + h)) <= 1e-6:# 第三种情况y_min, y_max = y, y + helif func(x, y) < func(x, y + h):# 第一种情况y_max = y + hlamb = 1while func(x, y - lamb * h) < func(x, y):lamb += 1y_min = y - lamb * helse:# 第二组情况y_min = y + hlamb = 2while func(x, y + lamb * h) < func(x, y + h):lamb += 1y_max = y + lamb * hreturn y_min, y_max# 黄金分割法，求解x方向最优解
def golden_section_x(func, a, b, y, eps):# 统计迭代次数cnt = 0while b - a > eps:# 根据黄金分割法规则选择内部两点c = a + (b - a) * 0.382d = a + (b - a) * 0.618# 区间消去原理if func(c, y) < func(d, y):b = delse:a = ccnt += 1# 两点的中点定义为最优解return (a + b) / 2, func((a + b) / 2, y), cnt# 黄金分割法，求解y方向最优解
def golden_section_y(func, a, b, x, eps):# 统计迭代次数cnt = 0while b - a > eps:# 根据黄金分割法规则选择内部两点c = a + (b - a) * 0.382d = a + (b - a) * 0.618# 区间消去原理if func(x, c) < func(x, d):b = delse:a = ccnt += 1# 两点的中点定义为最优解return (a + b) / 2, func(x, (a + b) / 2), cnt# 坐标轮换法
def univariate_search(func, x, y, eps):# 打印初始值对应的解cur_best_f = func(x, y)iters = 0print('iter: {}, best_x: {}, best_y: {}, function calc: {}'.format(iters, x, y, cur_best_f))# 坐标轮换优化while True:iters += 1# x方向优化x_min, x_max = advance_and_retreat_x(func, x, y, 0.1)best_x, best_f, _ = golden_section_x(func, x_min, x_max, y, eps)print('iter_x: {}, best_x: {}, best_y: {}, best_f: {}'.format(iters, best_x, y, best_f))x = best_x# 退出循环判断if abs(best_f - cur_best_f) <= eps:break# 更新最优解cur_best_f = best_f# y方向优化y_min, y_max = advance_and_retreat_y(func, x, y, 0.1)best_y, best_f, _ = golden_section_y(func, y_min, y_max, x, eps)print('iter_y: {}, best_x: {}, best_y: {}, best_f: {}'.format(iters, x, best_y, best_f))y = best_y# 退出循环判断if abs(best_f - cur_best_f) <= eps:break# 更新最优解cur_best_f = best_freturn func(x, y)if __name__ == '__main__':# 实例fx_f, y_f, eps_f = 1, 2, 1e-3# 坐标轮换法计算最优解univariate_search(f, x_f, y_f, eps_f)print("===========================")# 实例gx_g, y_g, eps_g = -2, 2.2, 1e-3# 坐标轮换法计算最优解univariate_search(g, x_g, y_g, eps_g)

运行代码后，可以得到

iter: 0, best_x: 1, best_y: 2, function calc: 16
iter_x: 1, best_x: 2.000233763452192, best_y: 2, best_f: 14.000000109290703
iter_y: 1, best_x: 2.000233763452192, best_y: 0.00015399075125497154, best_f: 2.000000180430158
iter_x: 2, best_x: 1.9998462973783453, best_y: 0.00015399075125497154, best_f: 2.0000001183884457
===========================
iter: 0, best_x: -2, best_y: 2.2, function calc: 7.079999999999998
iter_x: 1, best_x: -1.311255594408947, best_y: 2.2, best_f: 1.8592504605100588
iter_y: 1, best_x: -1.311255594408947, best_y: 1.2040230144759103, best_f: -0.12451135087000331
iter_x: 2, best_x: -1.088311474688541, best_y: 1.2040230144759103, best_f: -0.45831207876525415
iter_y: 2, best_x: -1.088311474688541, best_y: 1.048100675705184, best_f: -0.5069639956625354
iter_x: 3, best_x: -1.0568821019967993, best_y: 1.048100675705184, best_f: -0.512672581153325
iter_y: 3, best_x: -1.0568821019967993, best_y: 1.0300634221854548, best_f: -0.5133235969440142

上述两个实例分别来源于实例1和实例2。对比原文的结果可知，最终结果都是吻合的，即本文的算法原理和代码实现是没有问题的。

坐标轮换法优缺点

针对多维最优化问题来说，坐标轮换法应该是非常容易理解和实现的解决方案。虽然文中的代码上不了台面，但是总归是比较容易实现的，而且全程只需要计算目标函数本身，并未引入导数等其他信息，所以计算速度非常快。

坐标轮换法的主要缺点是收敛效率很难保证。这里借网上大佬做的一张图来说明。以下三种为三类最优化问题的等高线图：针对第1种类型的问题，坐标轮换法在2次迭代后便得到了最优解；针对第2种类型的问题，6次迭代可以得到最优解；针对第三种类型的问题，坐标轮换法不收敛，无法得不到最优解。