用矩阵乘幂的方法，求斐波那契数列f(n)=f(n-1)+f(n-2)，不用递归求，速度非常非常快

用矩阵乘幂的方法，求斐波那契数列f(n)=f(n-1)+f(n-2)，不用递归求，速度非常非常快！

提示：矩阵A的p次幂的快速乘法，是重要的优化算法基础知识

之前的基础：咱们求过数字最快速乘幂的方法（数字a的p次幂），
（1）最快乘法：普通数字a的p次幂怎么求速度最快，不用Math.pow(a,p)哦
（2）咱们求过矩阵最快速乘幂的方法（矩阵A的p次幂），
最快矩阵乘法：矩阵A的p次幂怎么求速度最快，Math根本没有求矩阵的幂次函数

这俩知识点，你必须看懂，否则这个文章你看不懂！
这俩知识点，你必须看懂，否则这个文章你看不懂！
这俩知识点，你必须看懂，否则这个文章你看不懂！

今天我们用矩阵的乘幂来求斐波那契数列f(n)
之前咱们用暴力递归和动态规划的方法，求过斐波那契数列：
（3）斐波那契数列：暴力递归改动态规划

文章目录

• 用矩阵乘幂的方法，求斐波那契数列f(n)=f(n-1)+f(n-2)，不用递归求，速度非常非常快！
• • @[TOC](文章目录)
• 题目
• 一、笔试AC解：暴力递归和动态规划求斐波那契数列（面试能将动态规划那个解）
• 二、面试高超优化技巧：矩阵最快乘幂法求解
• 总结

题目

用矩阵乘幂的方法，求斐波那契数列f(n)=f(n-1)+f(n-2)，不用递归求，速度非常非常快

一、笔试AC解：暴力递归和动态规划求斐波那契数列（面试能将动态规划那个解）

之前咱们用暴力递归和动态规划的方法，求过斐波那契数列：
（3）斐波那契数列：暴力递归改动态规划
当时动态规划，就是填一个表，从1 2 填写到N，求dp[n]，上面那个文章，我就不在这重复了，你去看懂，很简单。

二、面试高超优化技巧：矩阵最快乘幂法求解

情况是这样的，有一个关于斐波那契数列的基础理论

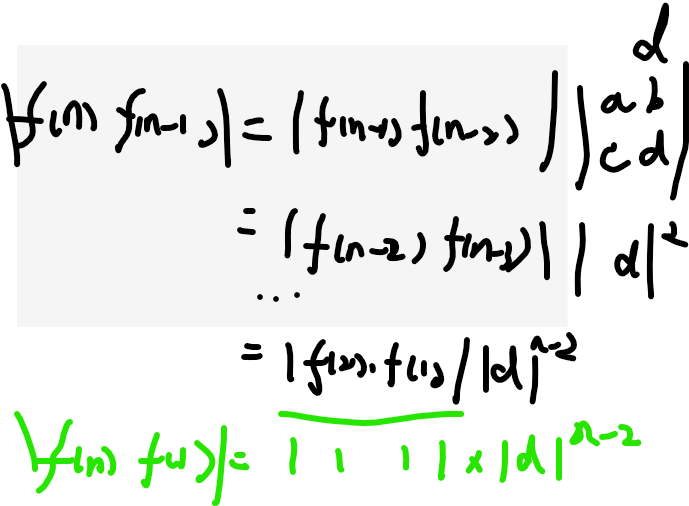
其实根据
n=1，f(n)=1
n=2，f(n)=1
n=3，f(n)=2
n=4，f(n)=5
……
可知：
上式子中的d矩阵为：

也就是说，斐波那契数列实际上有这么一个关系

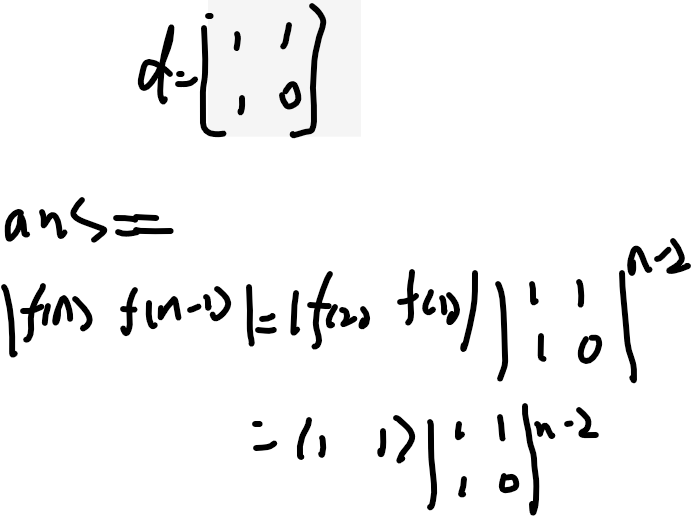
所以，咱们，只需要把d的n-2次幂求出来不就完事了吗
然后取f(n)=ans[0][0]即可！！

是不是很妙？？

你记住d就行，1110
这里就用到咱们的基础知识：
（2）咱们求过矩阵最快速乘幂的方法（矩阵A的p次幂），
最快矩阵乘法：矩阵A的p次幂怎么求速度最快，Math根本没有求矩阵的幂次函数
代码咱们直接贴过来用：

//C=A×B咋求public static int[][] matrixMul(int[][] A, int[][] B){int m = A.length;int b = B[0].length;int[][] C = new int[m][b];//A的一行，×B的一列，求和，放在C的m行，b列for (int i = 0; i < m; i++) {for (int j = 0; j < b; j++) {//A的一行，×B的一列，求和，放在C的m行，b列int ans = 0;for (int k = 0; k < A[0].length; k++) {//是A的列哦ans += A[i][k] * B[k][j];}C[i][j] = ans;}}return C;}//矩阵A的p次幂public static int[][] powMatrixAitsPCiMi(int[][] A, int p){int m = A.length;int n = A[0].length;//初始化，a=I，t=A的1次方int[][] a = new int[m][n];for (int i = 0; i < m; i++) {a[i][i] = 1;//单位阵}int[][] tmp = A;//基数矩阵//（1）p的0位x=1：a=a×t=1×A的1次方=A的1次方，t=t×t=A的2次方//（2）p的1位x=1：a=a×t=A的1次方=A的1次方×A的2次方，t=t×t=A的4次方//（3）p的2位x=0：~~a=a×t=A的1次方=A的1次方×A的2次方~~ ，t=t×t=A的8次方//（4）p的3位x=1：a=a×t=A的1次方=A的1次方×A的2次方×A的8次方，t=t×t=A的16次方//（5）p的4位x=0：~~a=a×t=A的1次方=A的1次方×A的2次方×A的8次方~~ ，t=t×t=A的32次方//（6）p的5位x=0：~~a=a×t=A的1次方=A的1次方×A的2次方×A的8次方~~ ，t=t×t=A的64次方//（7）p的6位x=1：a=a×t=A的1次方=A的1次方×A的2次方×A的8次方×A的64次方 ，t=t×t=A的128次方//此时a已经是A的p=75次方了//看p的x位是否为1for(; p != 0; p >>= 1){//每次结束p往右移动1位，p=0结束if ((p & 1) != 0){//p最右那个x位=1，需要雷×结果a = matrixMul(a, tmp);//a=a*t}//每次t都需要倍次幂tmp = matrixMul(tmp, tmp);//t=t*t}return a;//返回a}

下面咱们求：ans

手撕代码也很好理解

//求anspublic static int feiBoNaQiSeqReview(int n){if (n == 1) return 1;if (n == 2) return 1;int[][] m21 = {{1, 1}};//1*2矩阵哦//f2 f1 = 1 1int[][] d = {{1, 1},{1, 0}};//2*2矩阵哦//递归那个公式记住了//结果ans[0]=f(n)int[][] ans = matrixMul(m21, powMatrixAitsPCiMi(d, n - 2));return ans[0][0];}public static void test4(){System.out.println(feiBoNaQi2(5));System.out.println(feiBoNaQiSeqReview(5));}public static void main(String[] args) {test4();}

是不是超简单

5
5

这个矩阵幂次的求法，是不是跟递归不一样，速度贼快！

总结

提示：重要经验：

1）矩阵幂次求斐波那契数列适合在面试中秀一把，因为矩阵的幂次很快，这就是加速算法的高超技巧
2）斐波那契数列的递归矩阵公式，要记住，d=1110，方便怎么优化。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。