pytorch深度学习实践（二）：梯度下降算法详解和代码实现（梯度下降、随机梯度下降、小批量梯度下降的对比）

本文主要是介绍pytorch深度学习实践（二）：梯度下降算法详解和代码实现（梯度下降、随机梯度下降、小批量梯度下降的对比），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、梯度下降

1.1 公式与原理

1.1.1 cost(w)

cost为数据集中所有样本的误差值平方再求均值。

1.1.2 梯度

计算梯度时为所有样本的梯度。一个样本的梯度为: $gra{d}_i=2\ast x_i\ast (x_i\ast w_i-y_i)$，所有样本的梯度为所有样本的$gra{d}_i$的和求平均。

1.1.3 w的更新

一个epoch中：w会等到中所有的x和y都计算完平均值之后再更新。

1.2 训练过程可视化

一般正常的训练过程中cost function都是一直在波动中下降的，如果出现了cost先下降到最小然后又上升的情况（抛物线），则说明训练失败，一般的原因是因为学习率设置过大。

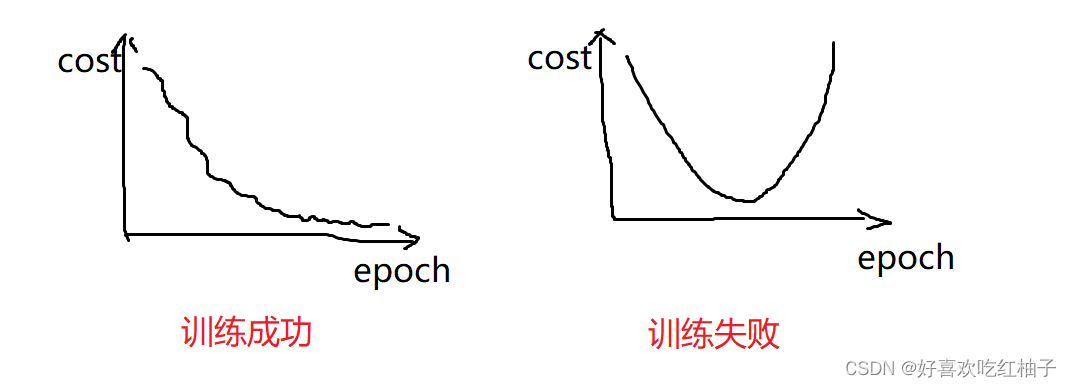
1.3 代码实现

import numpy as np
import matplotlib.pyplot as pltx_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w=1.0def forward(x):return x*wdef cost(xs,ys):cost = 0for x,y in zip(xs,ys):y_pred = forward(x)cost += (y_pred - y) ** 2return cost/len(xs)def gradient(xs,ys):grad = 0for x,y in zip(xs,ys):grad+= 2*x*(x*w-y)return grad/len(xs)w_list = []
cost_list = []
w_list.append(0.1)
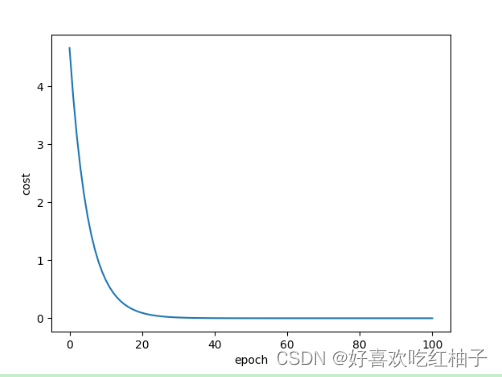
for epoch in range(101):cost_val = cost(x_data,y_data)grad_val = gradient(x_data,y_data)w-=0.01*grad_valw_list.append(w)cost_list.append(cost_val)print('Epoch:',epoch,'w=',w,'loss',cost_val)plt.plot(range(101),cost_list)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.show()

二、随机梯度下降（stochastic gradient descent，SDG）

2.1 公式与原理

随机梯度下降：从样本中随机抽出一组x和y，训练后按梯度更新一次，然后再抽取一组，再更新一次。

2.1.1 w的更新

计算一次$x_i$和$y_i$的梯度就进行一次参数更新。

一个epoch中：要进行样本个数次的参数更新

2.2 代码实现

import numpy as np
import matplotlib.pyplot as pltx_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w=1.0def forward(x):return x*wdef loss(x,y):return (forward(x)-y)**2def grad(x,y):return 2 * x * (x * w - y)loss_list = []
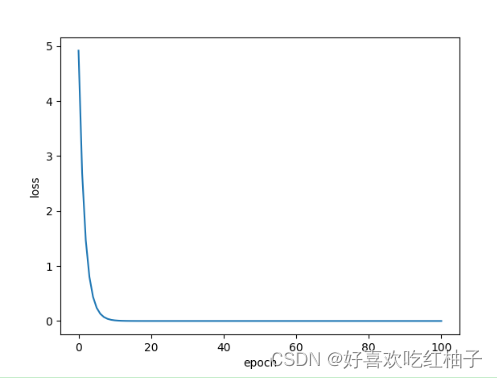
for epoch in range(101):for x,y in zip(x_data,y_data):w -= 0.01*grad(x,y)l = loss(x,y)loss_list.append(l)print("epoch=",epoch,"w=",w,"loss=",loss)plt.plot(range(101),loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

2.3 梯度下降和随机梯度下降的优缺点对比

2.3.1 梯度下降算法（Batch Gradient Descent）

优点：

收敛性较好： 梯度下降在每次迭代中使用整个训练集计算梯度，通常能够更快地收敛到较好的解；
稳定性高： 由于使用整个训练集计算梯度，梯度下降的更新方向相对稳定，能够更稳定地接近最优解；
可并行化： 由于每次迭代使用整个训练集，梯度下降可以更容易地进行并行化计算，加快训练速度。

缺点：

内存消耗大： 梯度下降需要在内存中保存整个训练集，对于大规模数据集来说，内存消耗较大；
计算代价高： 每次迭代都需要计算整个训练集的梯度，对于大规模数据集和复杂模型，计算代价较高；
容易陷入局部最优解：梯度下降可能会陷入局部最优解，特别是在非凸优化问题中。

2.3.2 随机梯度下降算法（Stochastic Gradient Descent）

优点：

计算代价低： 随机梯度下降每次迭代只使用一个样本计算梯度，因此计算代价较低；
内存消耗小：由于只需要一个样本，随机梯度下降的内存消耗相对较小；
可适用于在线学习：随机梯度下降适用于在线学习，可以动态地更新模型。

缺点：

收敛性相对较差： 由于梯度的随机性，随机梯度下降的收敛性较梯度下降差，可能会陷入波动或震荡；
不稳定：由于每次迭代只使用一个样本，随机梯度下降的更新方向相对不稳定，可能无法稳定地接近最优解；
学习率选择困难： 由于样本的随机性，随机梯度下降的学习率选择较为困难，需要进行合适的学习率调度。

三、小批量梯度下降（Mini-batch Gradient Descent）

结合BGD和SGD的优点，每一个epoch中取batchsize个样本进行梯度的更新。在每次迭代中随机均匀采样多个样本来组成一个小批量来计算梯度，一个epoch周期内会进行（样本数目/批量大小）次的参数更新。

3.1 优势

小批量梯度下降（Mini-batch Gradient Descent）是梯度下降和随机梯度下降的一种折衷方案，它同时具有一些梯度下降和随机梯度下降的优势，主要包括以下几点优势：

1. 较低的方差：相比于随机梯度下降，小批量梯度下降使用一小批样本来计算梯度，因此梯度估计的方差较低。 这使得小批量梯度下降相对更稳定，收敛性更好，并且可以更快地接近最优解。

2. 较高的计算效率：相比于梯度下降，小批量梯度下降每次迭代只使用一小批样本计算梯度，因此计算代价较低。这使得小批量梯度下降在处理大规模数据集时更具优势，能够更快地完成一轮迭代。

3. 更好的泛化性能：由于小批量梯度下降使用了一小批样本的信息，在每次迭代中能够更好地反映训练集的整体特点。这使得小批量梯度下降相对于随机梯度下降在一定程度上具有更好的泛化性能，可以得到更好的模型。

4. 并行化能力：小批量梯度下降的计算可以进行一定程度的并行化处理。由于每次迭代使用了一小批样本，可以将这些样本分配给不同的计算单元进行计算，从而提高训练速度。

3.2缺点

与梯度下降相比，由于每次迭代只使用了一小批样本，可能会引入一些噪声，导致更新方向相对不稳定。

小批量梯度下降需要选择合适的批大小，过小的批大小可能导致收敛速度变慢，而过大的批大小可能会增加计算代价和内存消耗。

3.3 代码实现

import numpy as np
import matplotlib.pyplot as pltx_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w=1.0
n=2
x_data_n = x_data[0:2]
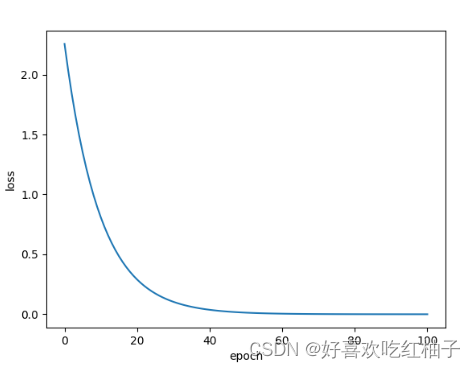
y_data_n = y_data[0:2]def forward(x):return x*wdef loss(x1,y1,n):loss = 0for x,y in zip(x1,y1):loss += (forward(x)-y)**2return loss/ndef grad(x1,y1,n):grad = 0for x, y in zip(x1, y1):grad += 2*x*(x*w-y)return grad/nloss_list = []for epoch in range(101):w-=0.01*grad(x_data_n,y_data_n,n)loss_list.append(loss(x_data_n,y_data_n,n))print("epoch=",epoch,"w=",w,"loss=",loss)plt.plot(range(101),loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

总结

现在多使用小批量随机梯度下降算法来进行梯度的更新。

这篇关于pytorch深度学习实践（二）：梯度下降算法详解和代码实现（梯度下降、随机梯度下降、小批量梯度下降的对比）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---