超详解的使用贪心算法解决TSP商旅问题（java）所谓TSP问题是指旅行家要旅行n个城市，要求各个城市经历且仅经历一次，并要求所走的路程 最短。该问题又称为货郎担问题，是图问题中最广为人知的问题

解题思想

如果对贪心算法还不理解的小伙伴，建议先了解下贪心算法的原理再来看看我的思路。

伪代码：
1.任意选择某个顶点v作为出发点
2.执行下述过程，直到所有顶点都被访问
2.1在顶点中v的邻接点中找到距离v最近且未被访问的邻接点j
2.2记录下v与j的距离
2.3访问j（以j作为顶点来寻找最近的邻接点）
3.从最后一个被访问的顶点回到出发点v

图解:
如图5x5矩阵（使用的大括号，将就一下，主要能够理解意思就好）。城市是从1开始计数的，也就是这里的城市编号为1-5.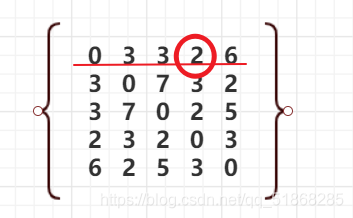

我们现在的出发点为第一个城市，因此我们要在第一个城市中找出距离最小且未被访问过的邻接点，可以通过遍历矩阵的第一行来获取最小的距离，也就是2，因此我们接下来会访问第4个城市，并将城市1标记为已访问，避免之后再遍历到城市1。

接着我们在城市4中寻找最小距离的城市，由于城市1我们已经访问过了，在这次遍历中便会直接跳过城市1，因此我们接下来要访问的城市是城市3，在访问城市3之前我们同样也要将城市4标记为已访问。

一直执行此操作直到所有的城市都被遍历完毕，这里可以用一个n（城市数量）大小的数组来记录所走的城市之间的距离，可以通过判断数组第n-1（数组下标为n-2的位置）的数是否为0来判断有没有访问这个城市。

为什么是判断n-1而不是判断第n个位置呢？
那是因为如果n个城市之间都走一遍的话，只会走n-1条路，所以判断数组的第n-1（下标为n-2）的位置是否为0，即可知道是否已经遍历完城市了，如果城市遍历完了，那么就可以退出循环，获取总的路径啦。不过别忘记要加上最后一段返回的路程哦。

源代码

package Demo06;import java.util.Scanner;public class TSPQuestion {public static void main(String[] args) {//输入城市个数int n;final int MAX = 1000000000;Scanner sc = new Scanner(System.in);n = sc.nextInt();//存储各城市之间的距离int[][] sd = new int[n][n];//用于存储距离int[] sq = new int[n];//用于表示sq已存的距离int top = 0;//用于表示该城市是否已经走过了(1表示已走，0表示未走过)int[] flag = new int[n];//为sq赋值for (int i = 0; i < n; i++) {sq[i] = MAX;}//构造城市距离的矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {sd[i][j] = sc.nextInt();}}//输入城市的起点(城市从1开始算，但数组构造的时候是从0开始的，因此还需要start-1)int start = sc.nextInt();System.out.print(start+"->");start = start-1;//记录起点城市，避免走到最后的时候无法找到起点了int firstCity = start;//记录下一个城市int nextCity = -1;//记录该城市是否已经被访问了，若已访问则为1，为访问则为0flag[start] = 1;//五个城市中，单项走不考虑回到起点的话，只有四条路//当sq已保存第四条路（也就是sq下标为n-2时）的距离的时候，退出循环，此时已走遍所有城市while (sq[n-2]==MAX) {//此处也可写top<n-1//遍历该城市与其他各个城市的距离for (int j = 0; j < n; j++) {//寻找出与该城市距离最小的邻接城市，且该城市未去过(如果输入为0则表示两条路不相通)if (sq[top] > sd[start][j] && flag[j] == 0&&sd[start][j]!=0) {sq[top] = sd[start][j];//用于记录邻接的城市nextCity = j;}}//当跳出循环的时候，则表示已经找到了该邻接城市//将该邻接城市标为已经到过flag[nextCity] = 1;//输出该邻接城市System.out.print((nextCity+1)+"->");//将邻接城市作为开头的城市，再次循环，直到所有的城市都被遍历过start = nextCity;//top++，表示sq的下一个空间用于存储下一段路top++;}System.out.print(firstCity+1);System.out.println();int sum =0;//sq的第五个空间用于存储最后一个地点与出发点的距离sq[n-1] = sd[firstCity][start];//得出已走过距离的总和for(int i = 0;i < n ;i++){sum += sq[i];}System.out.println("使用贪心算法获得的最短距离为：" + sum);}
}

运行截图：

总结

此方法仅供参考，仅记录我个人使用贪心算法来求解TSP商旅问题时所遇到的困惑及整体的解题思想，代码稍微有些简陋不过可读性较高，通俗易懂，希望能够帮助刚学数据结构的小白带来帮助。