代碼隨想錄算法訓練營|第四十五天|1049. 最后一块石头的重量 II、494. 目标和、474.一和零。刷题心得（c++）

本文主要是介绍代碼隨想錄算法訓練營|第四十五天|1049. 最后一块石头的重量 II、494. 目标和、474.一和零。刷题心得（c++），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

讀題

1049. 最后一块石头的重量 II

自己看到题目的第一想法

看完代码随想录之后的想法

494. 目标和

自己看到题目的第一想法

看完代码随想录之后的想法

474.一和零

自己看到题目的第一想法

看完代码随想录之后的想法

1049. 最后一块石头的重量 II - 實作

思路

Code

494. 目标和 - 實作

思路

Code

474.一和零 - 實作

思路

Code

總結

自己实现过程中遇到哪些困难

今日收获，记录一下自己的学习时长

相關資料

---

讀題

1049. 最后一块石头的重量 II

自己看到题目的第一想法

初始化定義，可以改成dp[j]代表重量為j 的狀態下，最小的數值為dp[j]，如果跟等和子集很像，那我的最大的背包重量應該是stone sum，但想了一陣子還是沒有想法，思緒非常不清晰。

看完代码随想录之后的想法

重量總和近似的兩堆，聽完就醍醐灌頂了，程式一下子就寫出來了，的去跟昨天的416很像，但是真的沒有想到是氛圍重量總和近似的兩堆，基本上有做過416，這一題就聽到這個關鍵字，基本就可以解出來了

494. 目标和

自己看到题目的第一想法

正與負可以想成取與不取，根據卡哥的遞推公式，還是沒有想得很清晰，到底可以怎麼做。

看完代码随想录之后的想法

• 拆解問題

將這個數組分成兩個子集，加法放一個集合(left)、減法放一個集合(right)

考慮’+’ 與 ‘-’ 的狀況下，公式如下

left + ( -right) = target → target 是題目提供的

left - right = target

不考慮’+’ 與 ‘-’ 的狀況下，公式如下

left + right = sum

這個等式可以改為

right = sum - left

將left 帶入考慮 ‘+’ & ‘-’的公式可以得到

left + left - sum = target

2 left = target + sum

left = (target + sum) / 2

因為target 跟 sum都是固定的

target 由題目提供

sum 透過數組總和得出

所以透過這兩個參數可以得出left這個變量需要為多少

• 轉換問題為01背包問題

在個問題題當中

正數總和 - 負數總和 = target 也就是 left - right = target

經過重新定義等式，可以得到上面所得出的公式

left = (target + sum) / 2

而left 實際上代表選擇的正數總和

所以問題轉化成: 如何從數組中選擇一些數字，使其總和為left

並且根據公式，可以發現target + sum / 2 是有可能不是正整數的

比如說target + sum = 5 那最後得到的left數字是 2.5

但我們在這個數組當中只有正整數，無法得到一個集合內的數字為2.5，也就是說無法得到一個解法，此時這個數組並沒有解法。

延伸出來講，回到公式定義 正數總和 - 負數總和 = target

這裡得負數總和不能想像成left - ( - right) = target

而是left - right = target ，不然思緒會感覺到混亂，會想說負負得正

但實際上所謂的負數總和根據題意也是正整數相加後套上一個 '-' 號

那假設target > sum 也就是目標值大於數組總和(全部都是正的) 那也無法得出一個解，因為這件事情在這個題意當中無法達成。

474.一和零

自己看到题目的第一想法

不太清楚要怎麼處理這樣的題目，看得有點矇

看完代码随想录之后的想法

原本的背包有只有一個維度，這次的背包有兩個維度需要考慮，並且因為物品的重量維度也有兩個，所以在處理上比較複雜，可以想像成是一個二維的滾動數組，背包滾動的過程比較繁瑣，需要考慮。

1049. 最后一块石头的重量 II - 實作

思路

<aside> 💡 分為兩堆近似重量的，兩者相撞就會是最小的。

</aside>

1. 定義DP數組以及下標的含意

   target: 假設分割為兩個的重量近似的兩堆

   dp[j] : 背包重量 j 的最大價值為dp[j]

   stones数組中，重量與價值就是stones[i]

2. 遞推公式

   dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

3. 根據遞推公式，確定DP數組如何初始化

   dp[0]要初始化為0，其他部分也要更新為正整數下的最小位数0

4. 確定遍歷順序

   避免覆蓋掉上一次的值，所以要使用倒敘遍歷

5. 打印dp數組 (debug);

Code

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(int i = 0; i < stones.size(); i++) {sum += stones[i];}int other = sum;sum /= 2;vector<int> dp(sum + 1, 0);for(int i = 0; i < stones.size(); i++) {for(int j = sum; j >= stones[i]; j--) {dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}int result = other - (dp[sum] + dp[sum]);return result;}
};

 

494. 目标和 - 實作

思路

<aside> 💡 之前的題目是求容量為j的背包，最多能裝多少。 這次的題目是求容量為j的背包，有多少方法可以裝滿。

</aside>

1. 定義DP數組以及下標的含意

   dp[j]: 容量為j的背包，有dp[j]個方法可以裝滿。

   dp[i][j]: 使用下標[0,i]個物品，在容量j的背包，有dp[i][j]種方法可以裝滿

2. 遞推公式

   其實轉換一下思路可以知道，之前求最大價值時，會去透過dp[j - weight[i]] + value[i] 的方法透過dp[j - weight[i]] 知道不包含目前重量的最大價值為多少

   那目標和dp[j - nums[i]] 可以背包j在不包含當前的nums[i]數值，有多少種方法可以裝滿 → dp[j - nums[i]]

   以及背包在包含當前nums[i]的數值，有多少種方法 → dp[j]

   公式會長成 dp[j] = dp[j] + dp[j - nums[i]]

   根據C++語法可以簡化為

   dp[j] += dp[j - nums[i]]

3. 根據遞推公式，確定DP數組如何初始化

   因為我們的問題轉化了，所以是要找出nums中有多少子集它的和為正數總和，所以我們就不能用原題意來看這道題目

   dp[0] 代表組成正數總和為0的方法有多少種，不選擇任何數字或者選取相互抵銷的正數或負數，但在初始化的過程當中並沒有選取任何數，可以想成說

   <aside> 💡 在不取任何數的狀況下，來思考有多少方法可以匹配dp數組的定義

   </aside>

   根據上面這個思路

   假設背包大小為三，其初始化數組應該如下

   dp[0] = 1

   dp[1] = 0

   dp[2] = 0

   因為不取任何數的狀況下，達成dp[0]的方法有1種，dp[1]~dp[2] 因為根本沒有取任何數，所以只有0種方法可以達成。

4. 確定遍歷順序

   根據遞推公式，外層迴圈是for 物品的變化取與不取，內層迴圈則是for 背包重量的變化由大到小進行遍歷。

5. 打印dp數組 (debug);

输入：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

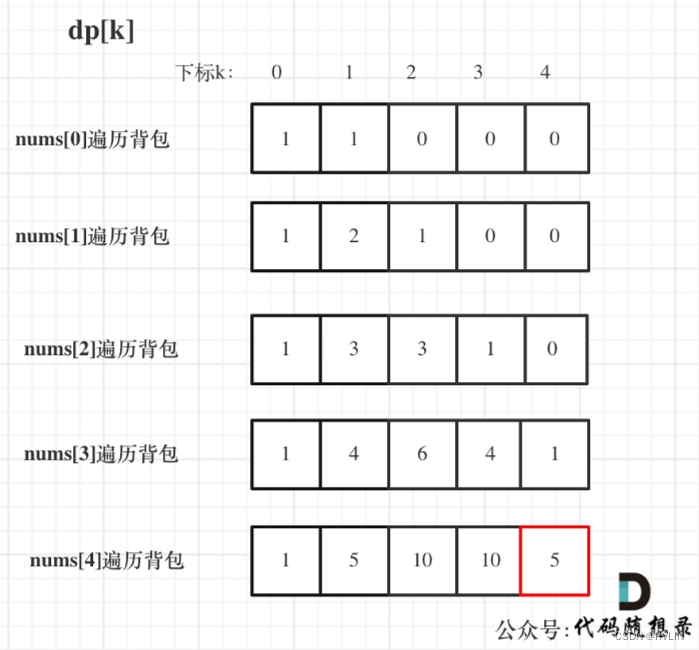
Code

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for(int i = 0; i < nums.size(); i++) {sum += nums[i];}if(abs(target) > sum) return 0;if((target + sum) % 2 == 1) return 0;int bagsize = (sum + target) / 2;vector<int> dp(bagsize + 1, 0);dp[0] = 1;for(int i = 0; i < nums.size(); i++ ) { //選擇物品for(int j = bagsize; j >= nums[i]; j--) { //選擇背包dp[j] += dp[j - nums[i]];}}return dp[bagsize];}
};

 

474.一和零 - 實作

思路

<aside> 💡 題意中的m與n可以想像成是兩個維度的背包，物品也可以想成是有兩個維度的重量所組成

</aside>

1. 定義DP數組以及下標的含意

   dp[i][j]: i個0與j個1所組成的最大子集合為dp[i][j]

2. 遞推公式

   • 先處理物品重量
     • 每個字串由0跟1組成，計算其0，1的個別重量為zeroNum、oneNum
   • 遞推公式 dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1]

3. 根據遞推公式，確定DP數組如何初始化

   dp[0][0] = 0 代表沒有組合可以放入這個背包當中，其餘數組則初始化為0 避免影響結果

4. 確定遍歷順序

   先遍歷物品，在遍歷二維背包

   因為是滾動數組，所以二維背包是由後往前遍歷

Code

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp (m+1, vector<int>(n+1, 0));for(string str: strs) {int zeroNum=0, oneNum=0;for(char c: str) {if(c == '0') zeroNum++;else oneNum++;}for(int i = m; i >= zeroNum; i--) {for(int j = n; j >= oneNum; j--) {dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
};

總結

自己实现过程中遇到哪些困难

在實現的過程中，在494. 目标和，其實真的思考了很久到底要怎麼解，並且題解影片也看了好幾次，也透過了線上AI，不斷的去釐清自己的想法，最終才寫了出來，感覺這個過程中其實真的不容易，理解上要花很多時間才能夠完全吸收，但目前就是一刷，繼續加油!

今日收获，记录一下自己的学习时长

總共學習了4hr左右，不斷的去釐清自己的想法，最終終於釐清並且透過自己的語言寫下思路。

相關資料

● 今日学习的文章链接和视频链接

1049. 最后一块石头的重量 II

视频讲解：动态规划之背包问题，这个背包最多能装多少？LeetCode：1049.最后一块石头的重量II_哔哩哔哩_bilibili

https://programmercarl.com/1049.最后一块石头的重量II.html

494. 目标和

视频讲解：动态规划之背包问题，装满背包有多少种方法？| LeetCode：494.目标和_哔哩哔哩_bilibili

https://programmercarl.com/0494.目标和.html

474.一和零

视频讲解：动态规划之背包问题，装满这个背包最多用多少个物品？| LeetCode：474.一和零_哔哩哔哩_bilibili

https://programmercarl.com/0474.一和零.html

 

这篇关于代碼隨想錄算法訓練營|第四十五天|1049. 最后一块石头的重量 II、494. 目标和、474.一和零。刷题心得（c++）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---