【Python量化】手把手教你用python做股票分析入门

内容来自：微信公众号：python金融量化
关注可了解更多的金融与Python干货。

目前，获取股票数据的渠道有很多，而且基本上是免费的，比如，行情软件有同花顺、东方财富等，门户网站有新浪财经、腾讯财经、和讯网等。Python也有不少免费的开源api可以获取交易行情数据，如pandas自带的库，tushare和baostock等。由于pandas库不再支持yahoo数据库后变得很不好用，而baostock最早记录的数据是2006年，因此本文主要讲讲如何使用tushare获取股票交易数据和可视化分析，tushare基本上记录了股票自上市之日起所有的日交易数据，是目前分析国内A股（支持其他非股票行情数据，如期货）比较好用的开源接口。

获取股票数据
01
使用tushare包的get_k_data()函数来获取股票交易数据，具体可以通过命令help(ts.get_k_data)了解函数和参数含义。

#先引入后面可能用到的包（package）
import pandas as pd  
import numpy as np
import matplotlib.pyplot as plt
#正常显示画图时出现的中文
from pylab import mpl
#这里使用微软雅黑字体
mpl.rcParams['font.sans-serif']=['SimHei']
#画图时显示负号
mpl.rcParams['axes.unicode_minus']=False
import seaborn as sns  #画图用的
import tushare as ts
#Jupyter Notebook特有的magic命令
#直接在行内显示图形
%matplotlib inline    

02
小试牛刀：获取上证指数自发布以来的数据

sh=ts.get_k_data(code='sh',ktype='D',autype='qfq', start='1990-12-20')
#code:股票代码，个股主要使用代码，如‘600000’
#ktype:'D':日数据；‘m’：月数据，‘Y’:年数据
#autype:复权选择，默认‘qfq’前复权
#start：起始时间
#end：默认当前时间
#查看下数据前5行
sh.head(5)

能看到的第一列是索引，对于pandas的数据结构，最后将索引设置为时间序列，方便后面可视化分析。

#将数据列表中的第0列'date'设置为索引
sh.index=pd.to_datetime(sh.date) 
#画出上证指数收盘价的走势
sh['close'].plot(figsize=(12,6))
plt.title('上证指数1990-2018年走势图')
plt.xlabel('日期')
plt.show()

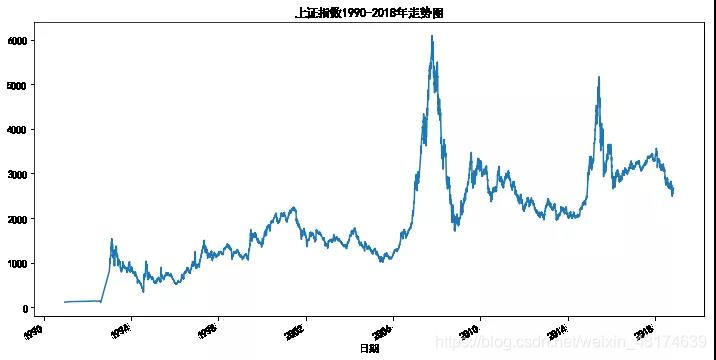
上面的指数走势图还是可以清晰看出，股指分别在2007年和2015年有两波大牛市，然后又从高峰跌入谷底，目前处于下跌通道。真是辛辛苦苦28年，一夜回到解放前o(╥﹏╥)o

描述性统计

#pandas的describe()函数提供了数据的描述性统计
#count:数据样本，mean:均值，std:标准差
sh.describe().round(2)

结果如下表所示：

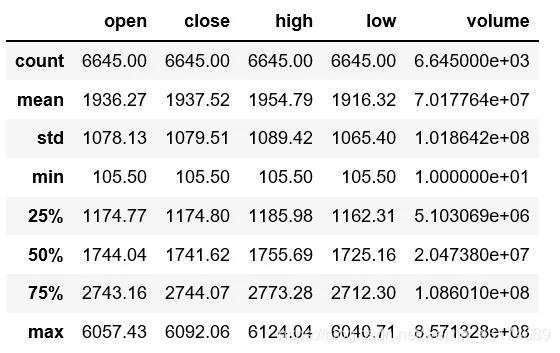
从上述结果可以看出，上证指数从1990年12月20日至2018年11月7日（最后交易日是当前运行时间），一共有6645个样本，均值为1937.52点，标准差为1079.51点（波动还是比较大的），最大值是6092.06点。

#再查看下每日成交量 
#2006年市场容量小，交易量比较小，我们从2007年开始看
sh.loc["2007-01-01":]["volume"].plot(figsize=(12,6))
plt.title('上证指数2007-2018年日成交量图')
plt.xlabel('日期')
plt.show()

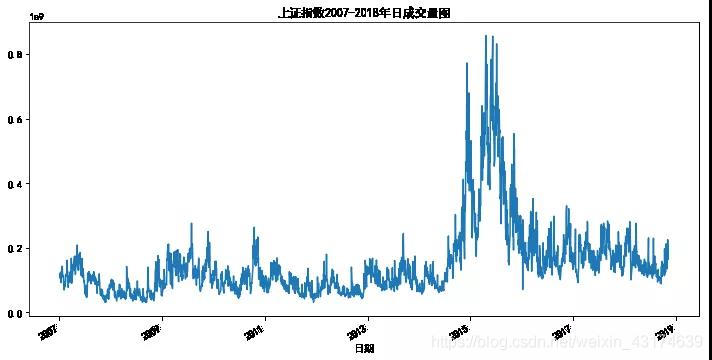
上图的成交量反映了一个有趣的现象，2014-2015年的大牛市很可能是天量的交易推动起来的，因为这期间实体经济并不景气，央行多次降息降准，货币宽松，资金流入股市，银行理财等影子银行在这期间疯狂扩张，场外加杠杆和配资主导了这一场牛市。感兴趣的朋友可以结合货币供给、实体经济指标、影子银行等数据一起分析，进行交叉验证。

均线分析

#这里的平均线是通过自定义函数，手动设置20,52,252日均线
#移动平均线：
ma_day = [20,52,252]for ma in ma_day:column_name = "%s日均线" %(str(ma))sh[column_name] =sh["close"].rolling(ma).mean()
#sh.tail(3)
#画出2010年以来收盘价和均线图
sh.loc['2010-10-8':][["close",
"20日均线","52日均线","252日均线"]].plot(figsize=(12,6))
plt.title('2010-2018上证指数走势图')
plt.xlabel('日期')
plt.show()

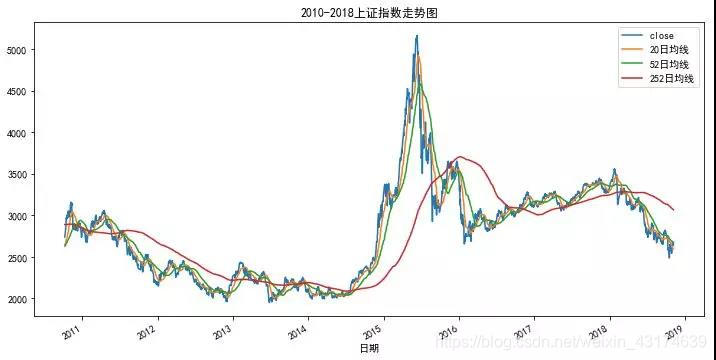
日收益率可视化

#2005年之前的数据噪音太大，主要分析2005年之后的
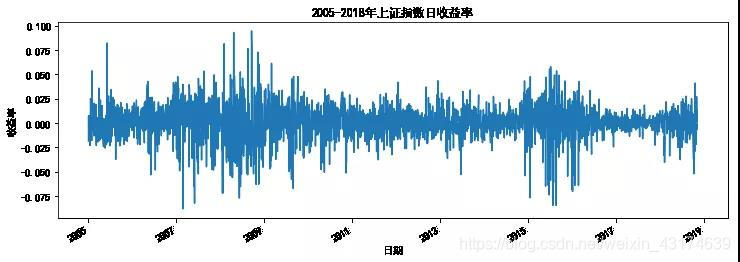
sh["日收益率"] = sh["close"].pct_change()
sh["日收益率"].loc['2005-01-01':].plot(figsize=(12,4))
plt.xlabel('日期')
plt.ylabel('收益率')
plt.title('2005-2018年上证指数日收益率')
plt.show()

###这里我们改变一下线条的类型
#(linestyle)以及加一些标记(marker)
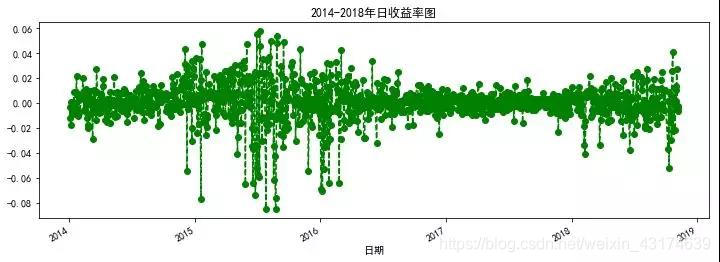
sh["日收益率"].loc['2014-01-01':].plot(figsize=
(12,4),linestyle="--",marker="o",color="g")
plt.title('2014-2018年日收益率图')
plt.xlabel('日期')
plt.show()

分析多只股票（指数）

#分析下常见的几个股票指数
stocks={'上证指数':'sh','深证指数':'sz','沪深300':'hs300','上证50':'sz50','中小板指':'zxb','创业板':'cyb'}
stock_index=pd.DataFrame()
for stock in stocks.values():stock_index[stock]=ts.get_k_data(stock,ktype='D', 
autype='qfq', start='2005-01-01')['close']
#stock_index.head()
#计算这些股票指数每日涨跌幅
tech_rets = stock_index.pct_change()[1:]
#tech_rets.head()
#收益率描述性统计
tech_rets.describe()
#结果不在此报告
#均值其实都大于0
tech_rets.mean()*100 #转换为%

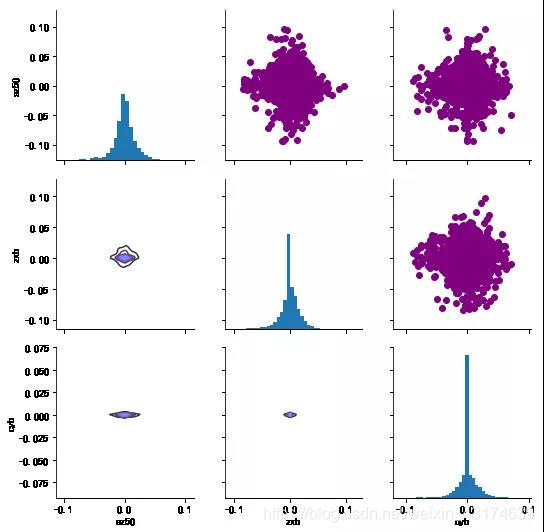
对上述股票指数之间的相关性进行可视化分析：

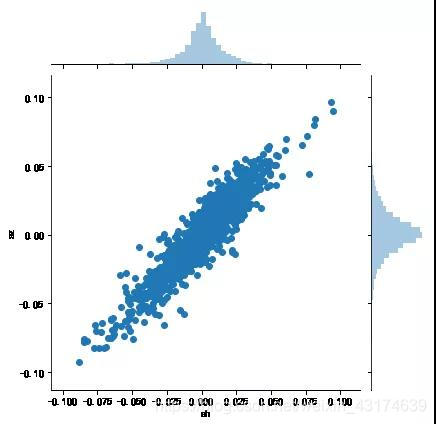
#jointplot这个函数可以画出两个指数的”相关性系数“，或者说皮尔森相关系数
sns.jointplot('sh','sz',data=tech_rets)

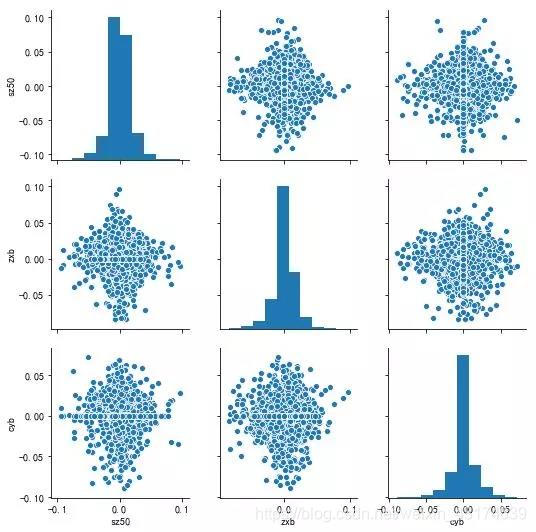
#成对的比较不同数据集之间的相关性，
#而对角线则会显示该数据集的直方图sns.pairplot(tech_rets.iloc[:,3:].dropna())

returns_fig = sns.PairGrid(tech_rets.iloc[:,3:].dropna())
###右上角画散点图
returns_fig.map_upper(plt.scatter,color="purple") 
###左下角画核密度图 
returns_fig.map_lower(sns.kdeplot,cmap="cool_d") 
###对角线的直方图 
returns_fig.map_diag(plt.hist,bins=30)

收益率与风险
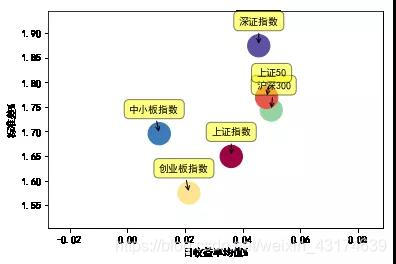
使用均值和标准分别刻画股票（指数）的收益率和波动率，对比分析不同股票（指数）的收益-风险情况。

#构建一个计算股票收益率和标准差的函数
#默认起始时间为'2005-01-01'
def return_risk(stocks,startdate='2005-01-01'):close=pd.DataFrame()for stock in stocks.values():close[stock]=ts.get_k_data(stock,ktype='D', autype='qfq', start=startdate)['close']tech_rets = close.pct_change()[1:]rets = tech_rets.dropna()ret_mean=rets.mean()*100ret_std=rets.std()*100return ret_mean,ret_std#画图函数
def plot_return_risk():ret,vol=return_risk(stocks)color=np.array([ 0.18, 0.96, 0.75, 0.3, 0.9,0.5])plt.scatter(ret, vol, marker = 'o', c=color,s = 500,cmap=plt.get_cmap('Spectral'))plt.xlabel("日收益率均值%")     plt.ylabel("标准差%")for label,x,y in zip(stocks.keys(),ret,vol):plt.annotate(label,xy = (x,y),xytext = (20,20),textcoords = "offset points",ha = "right",va = "bottom",bbox = dict(boxstyle = 'round,pad=0.5',fc = 'yellow', alpha = 0.5),arrowprops = dict(arrowstyle = "->",connectionstyle = "arc3,rad=0"))
stocks={'上证指数':'sh','深证指数':'sz','沪深300':'hs300','上证50':'sz50','中小板指数':'zxb','创业板指数':'cyb'}
plot_return_risk()

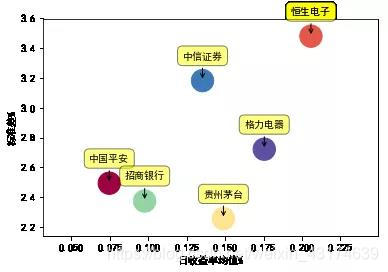
stocks={'中国平安':'601318','格力电器':'000651','招商银行':'600036','恒生电子':'600570','中信证券':'600030','贵州茅台':'600519'}
startdate='2018-01-01'
plot_return_risk()

蒙特卡洛模拟分析
蒙特卡洛模拟是一种统计学方法，用来模拟数据的演变趋势。蒙特卡洛模拟是在二战期间，当时在原子弹研制的项目中，为了模拟裂变物质的中子随机扩散现象，由美国数学家冯·诺伊曼和乌拉姆等发明的一种统计方法。之所以起名叫蒙特卡洛模拟，是因为蒙特卡洛在是欧洲袖珍国家摩纳哥一个城市，这个城市在当时是非常著名的一个赌城。因为赌博的本质是算概率，而蒙特卡洛模拟正是以概率为基础的一种方法，所以用赌城的名字为这种方法命名。蒙特卡洛模拟每次输入都随机选择输入值，通过大量的模拟，最终得出一个累计概率分布图。

df=ts.get_k_data('sh',ktype='D', autype='qfq', start='2005-01-01')
df.index=pd.to_datetime(df.date)
tech_rets = df.close.pct_change()[1:]
rets = tech_rets.dropna()
#rets.head()
#下面的结果说明，我们95%的置信，一天我们不会损失超过0.0264...
rets.quantile(0.05)
-0.026496813699825043

构建蒙特卡洛模拟函数：

def monte_carlo(start_price,days,mu,sigma):dt=1/daysprice = np.zeros(days)price[0] = start_priceshock = np.zeros(days)drift = np.zeros(days)for x in range(1,days):shock[x] = np.random.normal(loc=mu * dt,scale=sigma * np.sqrt(dt))drift[x] = mu * dtprice[x] = price[x-1] + (price[x-1] *(drift[x] + shock[x]))return price
#模拟次数
runs = 10000
start_price = 2641.34 #今日收盘价
days = 252
mu=rets.mean()
sigma=rets.std()
simulations = np.zeros(runs)for run in range(runs):simulations[run] = monte_carlo(start_price,days,mu,sigma)[days-1]
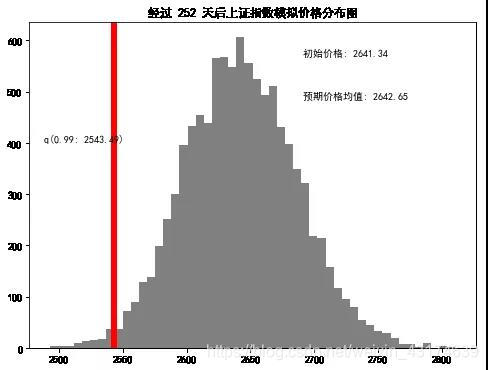
q = np.percentile(simulations,1)
plt.figure(figsize=(8,6))
plt.hist(simulations,bins=50,color='grey')
plt.figtext(0.6,0.8,s="初始价格: %.2f" % start_price)
plt.figtext(0.6,0.7,"预期价格均值: %.2f" %simulations.mean())
plt.figtext(0.15,0.6,"q(0.99: %.2f)" %q)
plt.axvline(x=q,linewidth=6,color="r")
plt.title("经过 %s 天后上证指数模拟价格分布图" %days,weight="bold")
Text(0.5,1,'经过 252 天后上证指数模拟价格分布图')

实际上蒙特卡洛模拟在期权定价里面还是很有用的。我们借用期权定价里对未来股票走势的假定来进行蒙特卡洛模拟。

import numpy as np
from time import time
np.random.seed(2018)
t0=time()
S0=2641.34
T=1.0; 
r=0.05; 
sigma=rets.std()
M=50;
dt=T/M; 
I=250000
S=np.zeros((M+1,I))
S[0]=S0
for t in range(1,M+1):z=np.random.standard_normal(I)S[t]=S[t-1]*np.exp((r-0.5*sigma**2)*dt+sigma*np.sqrt(dt)*z)
s_m=np.sum(S[-1])/I
tnp1=time()-t0
print('经过250000次模拟，得出1年以后上证指数的预期平均收盘价为：%.2f'%s_m)
经过250000次模拟，得出1年以后上证指数的预期平均收盘价为：2776.85
%matplotlib inline
import matplotlib.pyplot as plt
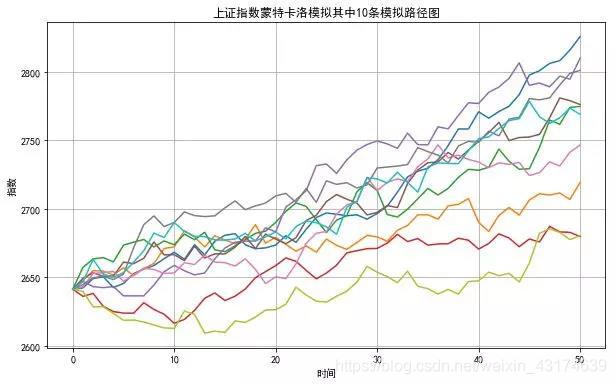
plt.figure(figsize=(10,6))
plt.plot(S[:,:10])
plt.grid(True)
plt.title('上证指数蒙特卡洛模拟其中10条模拟路径图')
plt.xlabel('时间')
plt.ylabel('指数')
plt.show()

plt.figure(figsize=(10,6))
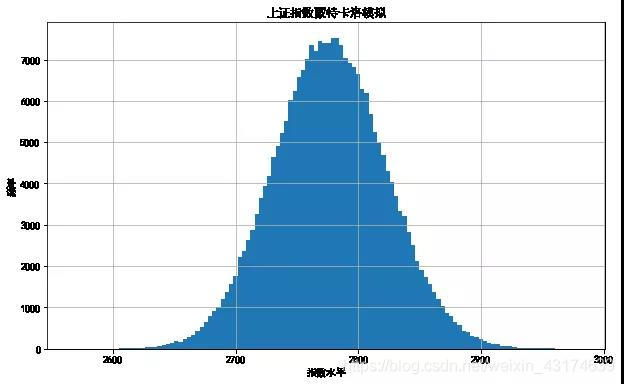
plt.hist(S[-1], bins=120)
plt.grid(True)
plt.xlabel('指数水平')
plt.ylabel('频率')
plt.title('上证指数蒙特卡洛模拟')
Text(0.5,1,'上证指数蒙特卡洛模拟')

THE END

本文主要介绍了如何使用Python获取股票数据，并进行简单的统计分析和可视化，综合运用了Python金融量化分析的Pandas、NumPy和Matplotlib等包。目前，A股处于至暗时刻，或许是学习和历练的最好时机，涅槃重生的过程总是艰难的，但振翅飞翔的一刻值得你等待。