人工智能经典问题，八数码问题求解，启发式搜索法(Astar算法)，C语言版，保证看懂，分析到位，注释详细，没有bug

一、问题描述

1. 3*3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空。
2. 要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态（图左）到目标状态（图右）。

二、迟来的代码

// 备注：曼哈顿距离等于当前状态与目标状态的水平距离和垂直距离之和#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>#define N 	3	// 阶数，可以改为更高阶// 定义一个结构体来表示棋盘状态
typedef struct node
{int cost;			// 从初始状态到本状态的代价int data[N][N];		// 存放棋盘状态struct node *prev;	// 链表中的前指针struct node *next;	// 链表中的后指针struct node *father;// 搜索树的父节点
}node;node *open;			// open表，存放未拓展的节点
node *close;		// close表，存放已经拓展的节点
static int n = 0;	// 用来记录总共搜索的次数int src[N][N] = {2, 8, 3, 1, 0, 4, 7, 6, 5};	// 初始状态
int cur[N][N];	// 当前状态
int dest[N][N] = {1, 2, 3, 8, 0, 4, 7, 6, 5};	// 目标状态// 生成一个节点
node *initList()
{int i, j;node *p = malloc(sizeof(node));if(!p){printf("malloc fail\n");return NULL;}p->prev = p;p->next = p;p->father = NULL;p->cost = 0;// 初始化棋盘状态for(i = 0; i < N; i++){for(j = 0; j < N; j++){p->data[i][j] = -1;}}return p;
}// 头插法，把节点插入到链表头部
void head_insert(node *head, node *p)
{p->next = head->next;p->prev = head;head->next->prev = p;head->next = p;
}// 尾插法，把节点插入到链表尾部
void tail_insert(node *head, node *p)
{p->prev = head->prev;head->prev->next = p;p->next = head;head->prev = p;
}// 弹出节点
void Remove(node *p)
{p->prev->next = p->next;p->next->prev = p->prev;p->next = p;p->prev = p;
}// 清空链表
void clearList(node *head)
{// 空表不需要再清空if(!head || head->next == head){printf("list is null\n");return;}// 头删法，跟头插法相似，循环删除首元节点for(node *p = head->next; p != head; p = head->next){Remove(p);  // 弹出节点pfree(p);    // 释放节点p的空间}
}// 初始化棋盘
void init()
{int i, j, k;int a[N*N] = {1, 2, 3, 8, 0, 4, 7, 6, 5};int flag[N*N] = {0};	// 用来标记0~8中哪个数字已经出现过srand(time(0));for(i = 0; i < N; i++){for(j = 0; j < N; j++){// 尝试生成一个0~8间的数字k = rand()%(N*N);while(1){// 如果该数字未出现if(flag[k] == 0)	{flag[k] = 1;	// 修改标志位src[i][j] = a[k]; // 初始化对应src的位置break;}// 重新生成数字k = rand()%(N*N);}}	}
}// 复制棋盘状态
void copy(int source[N][N], int dest1[N][N])
{int i, j;for(i = 0; i < N; i++){for(j = 0; j < N; j++){dest1[i][j] = source[i][j];}}
}// 打印棋盘状态
void display(int s[N][N])
{int i, j;for(i = 0; i < N; i++){for(j = 0; j < N; j++){// 把0当做空格输出if(s[i][j] > 0){printf("%d ", s[i][j]);}else if(s[i][j] == 0){printf("  ");}}printf("\n");}
}// 寻找出棋盘中的空格键
void findSpace(int s[N][N], int *x, int *y)
{int i, j;for(i = 0; i < N; i++){for(j = 0; j < N; j++){if(s[i][j] == 0)	// 找到空格{*x = i;*y = j;}}}
}// 空格上移
void up(int s[N][N], int x, int y)
{// 空格必须是处于第2行或者第3行，才能上移if(x >= 1){s[x][y] = s[x-1][y];s[x-1][y] = 0;}
}// 空格下移
void down(int s[N][N], int x, int y)
{// 空格必须是处于第1行或者第2行，才能下移if(x <= 1){s[x][y] = s[x+1][y];s[x+1][y] = 0;}
}// 空格左移
void left(int s[N][N], int x, int y)
{// 空格必须是处于第2列或者第3列，才能左移if(y >= 1){s[x][y] = s[x][y-1];s[x][y-1] = 0;}
}// 空格右移
void right(int s[N][N], int x, int y)
{// 空格必须是处于第1列或者第2列，才能右移if(y <= 1){s[x][y] = s[x][y+1];s[x][y+1] = 0;}
}// 采用曼哈顿距离，计算从某个状态cmp到当前状态的代价
// 曼哈顿距离指，与目标位置的水平距离和垂直距离之和
// 书上给出的代价是从起始节点S到任一节点i的路径代价g(i)
// 修改代价时，采用g(j) = g(i) + cost(i, j);
// cost(i, j)指从当前i节点到它的后继节点j的代价
// 但是这里因为每次空格操作，只会改变2个位置
// 所以cost(i, j)都相同，因此可以省略，直接计算g(j) 
void compute_cost(node *p, int cmp[N][N])
{int i, j, m, n;for(i = 0; i < N; i++){for(j = 0; j < N; j++){// 如果有对应位置不匹配的// 则重头搜索出与cmp[i][j]匹配的p->data[m][n]if(p->data[i][j] != cmp[i][j]){for(m = 0; m < N; m++){for(n = 0; n < N; n++){// 搜索到与cmp[i][j]匹配的p->data[m][n]// 计算曼哈顿距离后立马结束搜索if(p->data[m][n] == cmp[i][j]){// 累加每个位置的曼哈顿距离p->cost += abs(m-i) + abs(n-j);m = N;	// 修改m值，结束搜索break;}}}}}}
}// 检查close表中是否有重复的状态
int checkSame(int cmp[N][N])
{int i, j;node *p;for(p = close->next; p != close; p = p->next){for(i = 0; i < N; i++){for(j = 0; j < N; j++){if(p->data[i][j] != cmp[i][j]){i = N + 1;break;}}}if(i == N && j == N){return 1;}}return 0;
}// 检查当前棋盘状态是否为目标状态
int checkWin()
{int i, j;for(i = 0; i < N; i++){for(j = 0; j < N; j++){// 检测到有不同的就立马返回，节省时间if(cur[i][j] != dest[i][j]){return 0;}}}return 1;
}// 打印从初始状态到目标状态的路径
void showWin()
{int i = 1;node *p, *win;// 创建一个win表，用来存放路径win = initList();	if(!win){printf("win malloc fail\n");return;}// 由于节点中只有father(父节点)，而打印路径是从父节点开始的// 所以必须先从close表选择出正确的路径，因为close中可能存放不是正确路径的节点// 可以唯一确定的是 close->prev 一定是目的状态，由此循环往上寻找其父节点for(p = close->prev; p && p != close; p = p->father){Remove(p);	// 从close表中弹出p节点head_insert(win, p);	// 把p节点用头插法插入到win表中}printf("the solution as follow:\n");// 经过头插法创建的win表，一定是按从初始状态到目标状态的排序的for(p = win->next; p != win; p = p->next, i++){printf("step %d:\n", i);display(p->data);printf("\n");}clearList(win); // 清空win表free(win);      // 内存回收
}// 把当前节点(tmp) 的后继节点插入到open表中
void add(node *tmp, int cmp[N][N])
{node *p = initList();if(!p){printf("malloc fail\n");return;}copy(cmp, p->data);	// 复制棋盘状态p->father = tmp;	// 修改父节点指针compute_cost(p, src);	// 修改从初始状态到当前状态的代价compute_cost(p, dest);	// 修改从当前状态到目标状态的代价head_insert(open, p);	// BFS用尾插法，DFS用头插法
}// 从表中选择一个节点，使其代价p->cost最小
// 通常是从open表中选择，如果有多个点，则随便选一个
node *min_cost(node *head)
{// 空表直接退出if(!head || head->next == head){return NULL;}node *p, *min;min = head->next; for(p = min->next; p != head; p = p->next){if(p->cost < min->cost){min = p;}}return min;
}// 等代价搜索法
void Astar()
{printf("start Astar\n");node *tmp;int x, y, k, cmp[N][N];add(NULL, src);	// 把初始状态加入到open表中while(1){// 如果open表为空，就可以退出了if(open->next == open){printf("fail\n");return;}// 从open表中选择一个节点，使其代价p->cost最小tmp = min_cost(open);// 如果tmp为空，则说明open表为空// 但是一般不会出现，因为前面已经对open表进行判空处理// 这里写的原因就是特意为了增强算法的健壮性if(!tmp)	{printf("fail\n");return;}Remove(tmp);tail_insert(close, tmp);printf("now go :%d\n", ++n);// 打印当前搜索出的棋盘状态copy(tmp->data, cur);printf("current:\n");display(cur);// 检测当前棋盘状态是否为目标状态if(checkWin()){printf("success\n\n");printf("solution as follow:\n");showWin();return;}k = 0;	// 记录当前节点的后继节点个数findSpace(cur, &x, &y);	// 寻找当前棋盘状态的空格坐标printf("try up\n");// 空格必须是处于第2行或者第3行，才能上移if(x >= 1){copy(cur, cmp);	// 先复制当前状态cur到cmp中up(cmp, x, y);	// cmp尝试向上移// 判断cmp上移后close表中是否有重复状态// 没有重复才可以把cmp状态加入到close表中if(checkSame(cmp) == 0){k++;	// 当前节点的后继节点数加一add(tmp, cmp); // 把后继节点加入到open表中printf("can up\n");}}printf("try down\n");// 空格必须是处于第1行或者第2行，才能下移if(x <= 1){copy(cur, cmp);		// 先复制当前状态cur到cmp中down(cmp, x, y);	// cmp尝试向下移// 判断cmp下移后close表中是否有重复状态// 没有重复才可以把cmp状态加入到close表中if(checkSame(cmp) == 0){k++;	// 当前节点的后继节点数加一add(tmp, cmp); // 把后继节点加入到open表中printf("can down\n");}}printf("try left\n");// 空格必须是处于第2列或者第3列，才能左移if(y >= 1){copy(cur, cmp);		// 先复制当前状态cur到cmp中left(cmp, x, y);	// cmp尝试向左移// 判断cmp左移后close表中是否有重复状态// 没有重复才可以把cmp状态加入到close表中if(checkSame(cmp) == 0){k++;	// 当前节点的后继节点数加一add(tmp, cmp); // 把后继节点加入到open表中printf("can left\n");}}printf("try right\n");// 空格必须是处于第1列或者第2列，才能右移if(y <= 1){copy(cur, cmp);		// 先复制当前状态cur到cmp中right(cmp, x, y);	// cmp尝试向右移// 判断cmp右移后close表中是否有重复状态// 没有重复才可以把cmp状态加入到close表中if(checkSame(cmp) == 0){k++;	// 当前节点的后继节点数加一add(tmp, cmp); // 把后继节点加入到open表中printf("can right\n");}}// 如果当前状态没有后继节点，应该从close表中删除该状态if(k == 0){Remove(tmp);	// 弹出当前状态free(tmp);		// 释放当前状态printf("del done\n\n");}}
}int main()
{open = initList();	// 初始化open表close = initList(); // 初始化close表if(!open || !close){printf("初始化状态失败\n");return  -1;}// 测试阶段建议直接定义src, init()后的src很大程度上无解// init();	printf("src:\n");display(src);Astar();// 清空open表和close表并回收内存clearList(open);clearList(close);free(open);free(close);printf("DFS finish\n");return 0;
}

 运行截图

三、简单分析

        如果认真且仔细看完代码的程序猿同学，根据注释的讲解，可以说基本上可以看懂了，下面再来讲解一下算法的流程图和关键易错点。

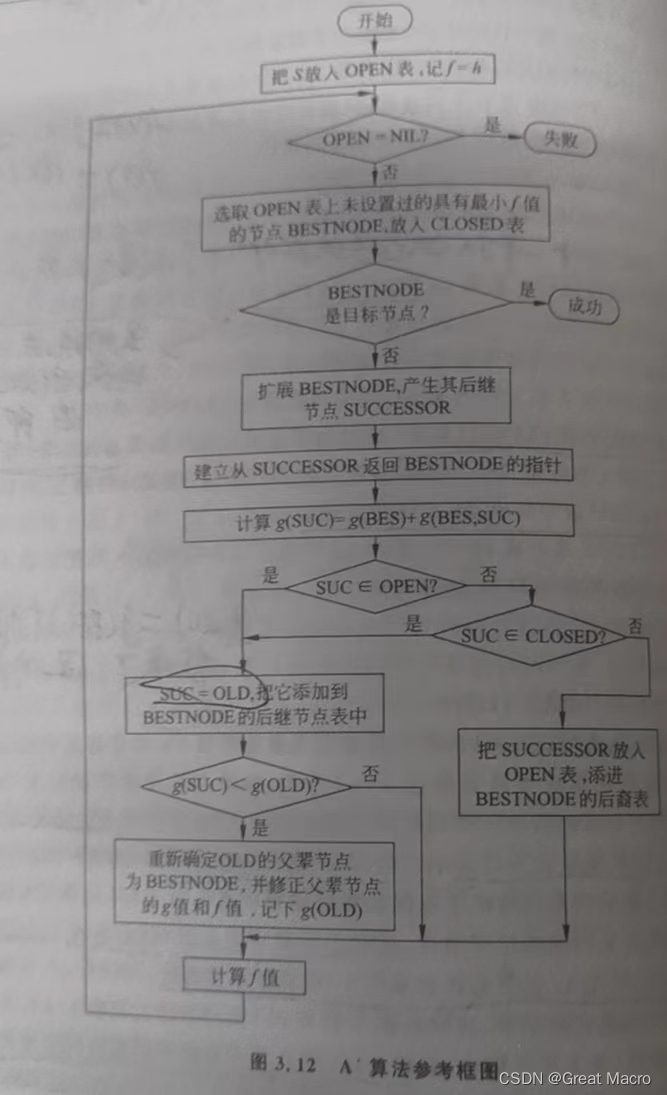
        流程图：

         关键易错点：

        1、open表用来存放未拓展的节点，close表用来存放已经拓展的节点，所以说，解的路径存放在close表中，但并不一定完全是close表中的节点，因为有些是其他不符合的节点。

        2、注意区分节点中的数据结构，一个版本中father指针的作用是保留父节点的指针，方便打印解的路径，而prev和next的作用是用来方便节点在链表中的操作，所以说，可以采用数组的方式来存储，此时就不需要prev和next指针了，这里不详细展开。

        3、算法结束的条件是：open表为空，即不存在任何后继节点了，此时为无解；或者当前状态就是目标状态，即找到了正确的解。

        4、空格操作的选择顺序：算法中对上移，下移，左移，右移的先后顺序要统一，不同的上下左右移动顺序会影响解的路径的长度，这点需要程序猿同学自己画图理解一下，这里比较难说明。

        5、如果存在解，则解的路径可能有多条，而使用BFS一定可以打印出一条最优解，注意用词是打印，不是搜索的过程是最优，而如果使用DFS则不一定可以打印出一条最优解，如果使用A*算法（启发式搜索）则可以保证搜索过程是最优的，自然就可以打印出一条最优解。

        6、启发式搜索，每次总是选择最有希望的节点加以拓展。这里的代价计算为:从初始状态到当前状态的代价和当前状态到目标状态的代价之和，代价采用曼哈顿距离计算。

        7、曼哈顿距离指，状态i与状态j之间水平距离和垂直距离之和。

四、小小总结

        本期八数码启发式搜索求解做的有点急，但是给的代码中有一些编程小技巧，细心的可以看出来，记得收藏起来，下期出八数码A*算法求解, 敬请关注！^_^